2017年度中考数学一模试题（北京市东城区） 13页

北京市东城区2014年中考一模数学试题 学校 班级 姓名 考号 ‎ 考 生 须 知 ‎1.本试卷共6页，共五道大题，25道小题，满分120分.考试时间120分钟.‎ ‎2.在试卷和答题卡上认真填写学校、班级、姓名和考号.‎ ‎3.试题答案一律填涂或书写在答题卡上，在试卷上作答无效.‎ ‎4.在答题卡上，选择题、作图题用2B铅笔作答，其他试题用黑色字迹签字笔作答.‎ ‎5.考试结束，请将本试卷、答题卡一并交回.‎ 一、选择题（本题共32分，每小题4分）‎ 下面各题均有四个选项，其中只有一个是符合题意的.‎ ‎1.的绝对值是 ‎ A. 5 B. C. D. -5‎ ‎2. 从财政部公布的2014年中央公共财政预算支出结构中，交通运输支出约为4350亿元，比去年同期增长7.1%.将4 350用科学记数法表示应为 ‎ A. 4.35‎×103 B. 0.435×‎104 C. 4.35×104 D. 43.5×102‎ ‎3．一个多边形的每个外角都等于72°，则这个多边形的边数为 ‎　‎ A．‎ ‎5‎ B．‎ ‎6‎ C．‎ ‎7‎ D．‎ ‎8‎ ‎4．有五张形状、大小、质地都相同的卡片，上面分别画有下列图形：①正方形；②正三角形；③平行四边形；④等腰梯形；⑤圆.将卡片背面朝上洗匀，从中随机抽取一张，正面图形既是轴对称图形，又是中心对称图形的概率是 A. B. C. D. ‎ ‎5. 在某校“我的中国梦”演讲比赛中，有9名学生参加决赛，他们决赛的最终成绩各不相同.其中的一名学生想要知道自己能否进入前5名，不仅要了解自己的成绩，还要了解这9名学生成绩的 A.众数 B.方差 C.平均数 D.中位数 ‎6. 如图，AB∥CD，点E在BC上，且CD=CE，∠D=74°，‎ 则∠B的度数为 A. 74° B. 32° ‎ C. 22° D. 16°‎ ‎7. 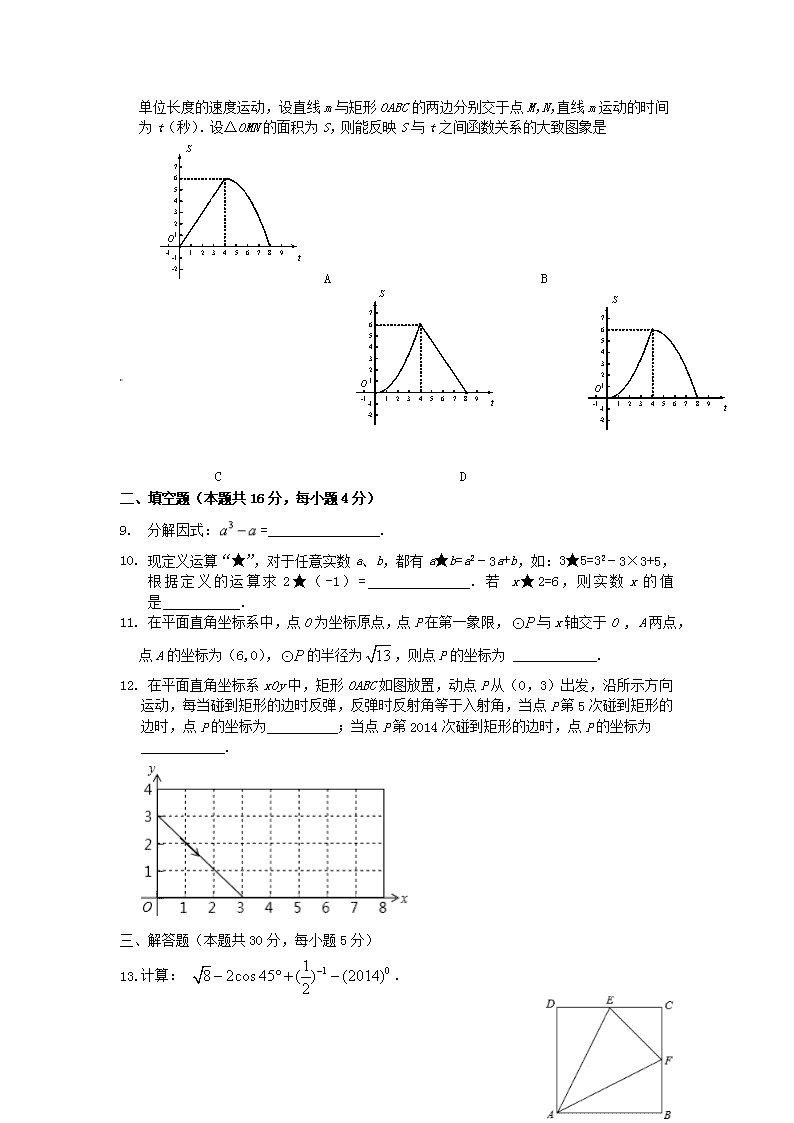若二次函数y=x2﹣2x+c的图象与y轴的交点为（0，﹣3），则此二次函数有 A.最小值为-2 B.最小值为‎-3 C.最小值为-4 D.最大值为-4‎ ‎ 8. 在平面直角坐标系中，四边形OABC是矩形，点B的坐标为（4，3）．平行于对角线AC的直线m从原点O出发，沿x轴正方向以每秒1‎ 个单位长度的速度运动，设直线m与矩形OABC的两边分别交于点M，N，直线m运动的时间为t（秒）．设△OMN的面积为S，则能反映S与t之间函数关系的大致图象是 A B ‎ ‎ C D 二、填空题（本题共16分，每小题4分）‎ ‎9. 分解因式：=________________.‎ ‎10. 现定义运算“★”，对于任意实数a、b，都有a★b=a2﹣‎3a+b，如：3★5=32﹣3×3+5，根据定义的运算求2★（-1）=　 ．若 x★2=6，则实数x的值是　 ．‎ ‎11. 在平面直角坐标系中，点O为坐标原点，点P在第一象限，与x轴交于O , A两点， 点A的坐标为（6,0），的半径为，则点P的坐标为 ____________.‎ ‎12. 在平面直角坐标系xOy中，矩形OABC如图放置，动点P从（0，3）出发，沿所示方向运动，每当碰到矩形的边时反弹，反弹时反射角等于入射角，当点P第5次碰到矩形的边时，点P的坐标为 ；当点P第2014次碰到矩形的边时，点P的坐标为____________.‎ 三、解答题（本题共30分，每小题5分）‎ ‎13.计算： ．‎ ‎14．求不等式组的最小整数解．‎ ‎15.已知：如图，正方形ABCD，E，F分别为DC，BC中点．‎ 求证：AE=AF．‎ ‎16．先化简，再求值： ，其中m是方程的根． ‎ ‎17.列方程或方程组解应用题 ‎ 某商店需要购进甲、乙两种商品共160件，其进价和售价如下表：(注:利润=售价-进价)‎ 甲 乙 进价(元/件)‎ ‎15‎ ‎35‎ 售价(元/件)‎ ‎20‎ ‎45‎ 若商店计划销售完这批商品后能使利润达到1100元，问甲、乙两种商品应分别购进多少件?‎ ‎18.如图，已知等腰△AOB放置在平面直角坐标系xOy中， OA=OB，点B的坐标为(3，4) .‎ ‎（1）求直线AB的解析式；‎ ‎（2）问将等腰△AOB沿x轴正方向平移多少个单位，能使点B落在反比例函数 （x＞0）的图象上.‎ 四、解答题（本题共20分，每小题5分）‎ ‎19. 如图，将一张矩形纸片ABCD沿直线MN折叠，使点C落在点A处，点D落在点E处，直线MN交BC于点M，交AD于点N．‎ ‎（1）求证：CM=CN；‎ ‎（2）若△CMN的面积与△CDN的面积比为3：1，且CD=4，求线段MN的长．‎ ‎20．某中学以“我最喜爱的书籍”为主题，对学生最喜爱的一种书籍类型进行随机抽样调查，收集整理数据后，绘制出以下两幅未完成的统计图，请根据图1和图2提供的信息，解答下列问题：‎ ‎（1）在这次抽样调查中，一共调查了多少名学生？‎ ‎（2）请把折线统计图（图1）补充完整；‎ ‎（3）求出扇形统计图（图2）中，体育部分所对应的圆心角的度数；‎ ‎（4）如果这所中学共有学生1800名，那么请你估计最喜爱科普类书籍的学生人数．‎ ‎21. 如图，AB是⊙O的直径，点E是上一点，∠DAC=∠AED．‎ ‎（1）求证：AC是⊙O的切线；‎ ‎（2） 若点E是的中点，连结AE交BC于点F，当BD=5， CD=4时，求DF的值．‎ ‎22. 阅读下面材料：‎ 小炎遇到这样一个问题：如图1，点E、F分别在正方形ABCD的边BC，CD上，∠EAF=45°，连结EF，则EF=BE+DF，试说明理由．‎ ‎ ‎ 图1 图2‎ ‎ 小炎是这样思考的：要想解决这个问题，首先应想办法将这些分散的线段相对集中．她先后尝试了翻折、旋转、平移的方法，最后发现线段AB，AD是共点并且相等的，于是找到解决问题的方法．她的方法是将△ABE绕着点A逆时针旋转90°得到△ADG，再利用全等的知识解决了这个问题（如图2）．‎ 参考小炎同学思考问题的方法，解决下列问题：‎ ‎（1）如图3，四边形ABCD中，AB=AD，∠BAD=90°点E，F分别在边BC，CD上，∠EAF=45°．若∠B，∠D都不是直角，则当∠B与∠D满足_ 关系时，仍有EF=BE+DF；‎ ‎（2）如图4，在△ABC中，∠BAC=90°，AB=AC，点D、E均在边BC上，且∠DAE=45°，若BD=1， EC=2，求DE的长．‎ 图3 图4‎ 五、解答题（本题共22分，第23题7分，第24题7分，第25题8分）‎ ‎23. 已知：关于x的一元二次方程mx2﹣（‎4m+1）x+‎3m+3=0 （m＞1）．‎ ‎（1）求证：方程有两个不相等的实数根；‎ ‎（2）设方程的两个实数根分别为x1，x2（其中x1＞x2），若y是关于m的函数，且y=x1﹣3x2，求这个函数的解析式；‎ ‎（3）将（2）中所得的函数的图象在直线m=2的左侧部分沿直线m=2翻折，图象的其余部分保持不变，得到一个新的图象．请你结合这个新的图象回答：当关于m的函数y=2m+b的图象与此图象有两个公共点时，b的取值范围．‎ ‎24. 如图1，已知∠DAC=90°，△ABC是等边三角形，点P为射线AD上任意一点（点P与点A不重合），连结CP，将线段CP绕点C顺时针旋转60°得到线段CQ，连结QB并延长交直线AD于点E.‎ ‎（1）如图1，猜想∠QEP= °；‎ ‎（2）如图2，3，若当∠DAC是锐角或钝角时，其它条件不变，猜想∠QEP的度数，选取一种情况加以证明；‎ ‎（3）如图3，若∠DAC=135°，∠ACP=15°，且AC=4，求BQ的长．‎ 图1 图2 图3‎ ‎25.在平面直角坐标系xOy中，直线分别与x轴，y轴交于过点A，B，点C是第一象限内的一点，且AB=AC，AB⊥AC，抛物线经过A，C两点，与轴的另一交点为D.‎ ‎（1）求此抛物线的解析式； ‎ ‎（2）判断直线AB与CD的位置关系，并证明你的结论；‎ ‎（3）点M为x轴上一动点，在抛物线上是否存在一点N，使以A,B,M,N四点构成的四边形为平行四边形？若存在，求点N的坐标；若不存在，请说明理由.‎ 北京市东城区2013--2014学年第二学期初三综合练习（一）‎ ‎ 数学试卷参考答案及评分标准 2014.5‎ 一、选择题（本题共32分，每小题4分） ‎ 题 号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ 答 案 B ‎ A ‎ A B D B C ‎ D 二、填空题（本题共16分，每小题4分）‎ 题 号 ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答 案 ‎﹣1或4‎ ‎(3,2)‎ ‎（1，4）‎ ‎（5,0）‎ 三、解答题：（本题共30分，每小题5分）‎ ‎13．（本小题满分5分）‎ 解：原式= ………………4分 ‎ =． ………………5分 ‎ ‎ ‎14．（本小题满分5分）‎ 解：解不等式 得＞2； ………………1分 解不等式 得≤8． ………………3分 ‎∴ 不等式组的解集为 2＜≤8． ………………4分 ‎∴ 不等式组的最小整数解为3． ………………5分 ‎15．（本小题满分5分）‎ 证明：∵ 四边形ABCD为正方形，‎ ‎∴ AB=AD，∠B=∠D=90°，DC=CB．………………2分 ‎∵ E、F为DC、BC中点，‎ ‎∴ DE=DC，BF=BC．‎ ‎∴ DE=BF． ………………3分 ‎∵ 在△ADE和△ABF中，‎ ‎∴ △ADE≌△ABF（SAS）． ………………4分 ‎∴ AE=AF． ………………5分 ‎16．（本小题满分5分） ‎ 解：原式=‎ ‎ =‎ ‎ =． ………………3分 ‎ ∵ m是方程的根，‎ ‎∴ ． ‎ ‎∴ ． ………………………5分 ‎17．（本小题满分5分） ‎ 解：设甲种商品应购进x件，乙种商品应购进y件. ………………………1分 ‎ 根据题意，得 ………………………3分 解得 ………………………4分 答：甲种商品购进100件，乙种商品购进60件. ………………………5分 ‎ ‎ ‎18.（本小题满分5分）‎ 解：（1）过点B作BC⊥x轴于点C.‎ 由勾股定理可得 .………1分 ‎∵ OA=OB，‎ ‎∴ 点A的坐标为（5,0）. ………2分 设直线AB的解析式为 .‎ ‎ 可求直线AB的解析式为.………3分 ‎（2）将等腰△AOB沿x轴正方向平移5个单位，能使点B落在反比例函数 ‎ ‎（x＞0）的图象上. ………5分 四、解答题（本题共20分，每小题5分）‎ ‎19.（本小题满分5分）‎ ‎（1）证明：由折叠的性质可得：∠ANM=∠CNM .‎ ‎ ∵ 四边形ABCD是矩形，‎ ‎ ∴ AD∥BC .‎ ‎ ∴ ∠ANM=∠CMN .‎ ‎ ∴ ∠CMN=∠CNM .‎ ‎ ∴ CM=CN. ………2分 ‎（2）解：过点N作NH⊥BC于点H，则四边形NHCD是矩形.‎ ‎ ∴ HC=DN，NH=DC.‎ ‎ ∵ △CMN的面积与△CDN的面积比为3：1，‎ ‎ ∴ MC=3ND=3HC.‎ ‎∴ MH=2HC.‎ 设DN=x，则HC=x，MH=2x，‎ ‎∴CM=3x=CN，‎ 在Rt△CDN中，DC=2x=4，‎ ‎∴ .‎ ‎∴ HM=2.‎ 在Rt△MNH中，MN=.‎ ‎20.（本小题满分5分）‎ 解：（1）90÷30%=300（名），‎ 一共调查了300名学生. ‎ ‎（2）艺术的人数：300×20%=60名，‎ 其它的人数：300×10%=30名；‎ 补全折线图如图.‎ ‎（3）体育部分所对应的圆心角的度数为：×360°=48°.‎ ‎（4）1800×=480（名）．‎ 答：1800名学生中估计最喜爱科普类书籍的学生人数为480．‎ ‎ ‎ ‎21．（本小题满分5分）‎ 解：（1）∵AB是⊙O的直径，‎ ‎∴∠ADB=∠ADC=90°．‎ ‎∵∠B=∠AED =∠CAD，∠C=∠C，‎ ‎∴∠BAC=∠ADC=90°．‎ ‎∴AC是⊙O的切线．………………2分 ‎（2）可证△ADC∽△BAC．‎ ‎∴ ．即AC2=BC×CD=36．‎ 解得 AC=6．‎ ‎∵点E是的中点，‎ ‎∴∠DAE=∠BAE.‎ ‎∵∠CAF=∠CAD+∠DAE=∠ABF+∠BAE=∠AFD，‎ ‎∴CA=CF=6，‎ ‎∴DF=CA﹣CD=2．………………5分 ‎22．（本小题满分5分）‎ 解： (1)∠B+∠D=180°（或互补）． ………………1分 ‎ (2)∵ AB=AC，‎ ‎∴ 把△ABD绕A点逆时针旋转90°至△ACG，可使AB与AC重合. ………………2分 ‎∠B=∠ACG,‎ ‎ BD=CG,‎ AD=AG ‎∵ △ABC中，∠BAC=90°，‎ ‎∴ ∠ACB+∠ACG=∠ACB+∠B=90°．‎ 即∠ECG=90°．‎ ‎∴ EC2+CG2=EG2．………………3分 在△AEG与△AED中,‎ ‎∠EAG=∠EAC+∠CAG=∠EAC+∠BAD=90°-∠EAD=45°=∠EAD．‎ 又∵AD=AG，AE=AE，‎ ‎∴ △AEG≌△AED ． ………………4分 ‎∴ DE=EG ．‎ 又∵CG=BD,‎ ‎∴ BD2+EC2=DE2． ‎ ‎ ∴ ．………………5分 五、解答题：（本题共22分，第23题7分，第24题7分，第25题8分）‎ ‎23．（本小题满分7分）‎ 解：（1）证明：‎ 所以方程有两个不等实根. ………………2分 ‎………………5分 ‎（3）作出函数的图象，并将图象在直线左侧部分沿此直线翻折，所得新图形如图所示.易知点的坐标分别为 当直线 过点 A 时，可求得 ‎ 过点B时，可求得 因此，‎ ‎ ……………7分 ‎24. （本小题满分7分）‎ 解： (1) ∠QEP= 60 °．………………1分 ‎ (2) ∠QEP= 60 °．‎ ‎ 证明: 如图1，以∠DAC是锐角为例．‎ ‎ ∵ △ABC是等边三角形，‎ ‎ ∴ AC=BC，∠ACB=60°．‎ ‎ 又由题意可知，CP=CQ，∠PCQ=6O°．‎ ‎ ∴ ∠ACP=∠BCQ．‎ ‎ ∴ △ACP≌△BCQ．‎ ‎ ∴ ∠APC=∠Q．‎ ‎ 设PC与BQ交于点G， 图1‎ ‎ ∵ ∠1=∠2，‎ ‎∴ ∠QEP=∠PCQ=60°． ………………4分 ‎（3）由题意可求，∠APC=30°，∠PCB=45°．‎ ‎ 又由（2）可证 ∠QEP=60°．‎ ‎ ∴ 可证QE垂直平分PC，‎ ‎△GBC为等腰直角三角形．‎ ‎ ∵ AC=4，‎ ‎ ∴ ，．‎ ‎∴ ． ………………7分 ‎ ‎ ‎25．（本小题满分8分）‎ 解：（1）由题意可求点A(2，0)，点B（0,1）.‎ 过点C作CE⊥x轴，易证△AOB≌△ECA.‎ ‎ ∴ OA=CE=2，OB=AE=1.‎ ‎ ∴ 点C的坐标为（3,2）. ………………1分 ‎ 将点A(2，0)，点C(3，2)‎ 代入，‎ 解得 ‎∴二次函数的解析式为. ………………2分 ‎(2)令，解得.‎ ‎∴ D点坐标为（7,0）.‎ 可求 .‎ ‎∴ △ACD为直角三角形，∠ACD=90°.‎ 又∵ ∠BAC=90°，‎ ‎∴ AB∥CD. ………………4分 ‎（3）如图，由题意可知，要使得以A,B,M,N四点构成的四边形为平行四边形，只需要点N到x轴的距离与点B到x轴的距离相等.‎ ‎∵ B点坐标为（0,1），‎ ‎∴ 点N到x轴的距离等于1.‎ 可得和.‎ 解这两个方程得.‎ ‎∴ 点N的坐标分别为（，1），（，1），（，-1），（，-1）. ………………8分