中考压轴题图形的变换 12页

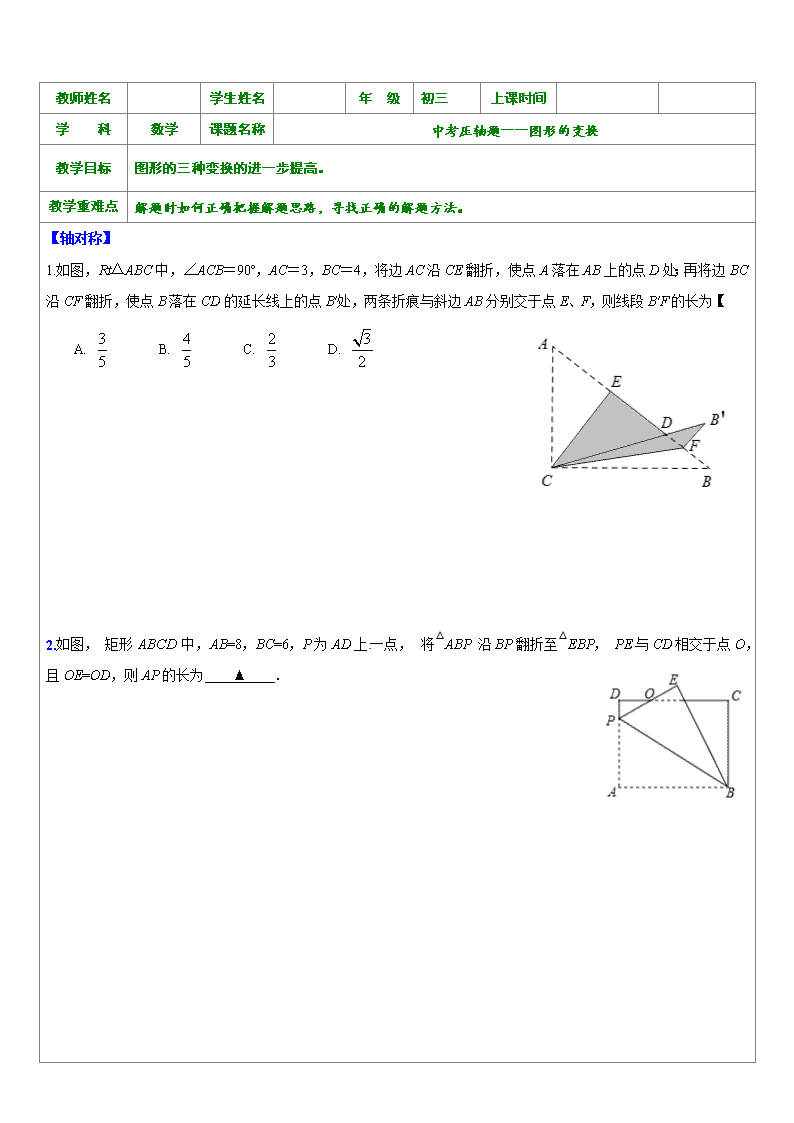
教师姓名 学生姓名 年 级 初三 上课时间 学 科 数学 课题名称 中考压轴题――图形的变换 教学目标 图形的三种变换的进一步提高。‎ 教学重难点 解题时如何正确把握解题思路，寻找正确的解题方法。‎ ‎【轴对称】‎ ‎1.如图，Rt△ABC中，∠ACB＝90º，AC＝3，BC＝4，将边AC沿CE翻折，使点A落在AB上的点D处；再将边BC沿CF翻折，使点B落在CD的延长线上的点B′处，两条折痕与斜边AB分别交于点E、F，则线段B′F的长为【 】‎ A. B. C. D. ‎ ‎2.如图， 矩形中，AB=8，BC=6，P为AD上一点， 将△ABP 沿BP翻折至△EBP， PE与CD相交于点O，且OE=OD，则AP的长为 ▲ ．‎ ‎【平移】‎ ‎1. 若函数的图像如图所示，则关于的不等式的解集为【 】‎ A. B. C. D. 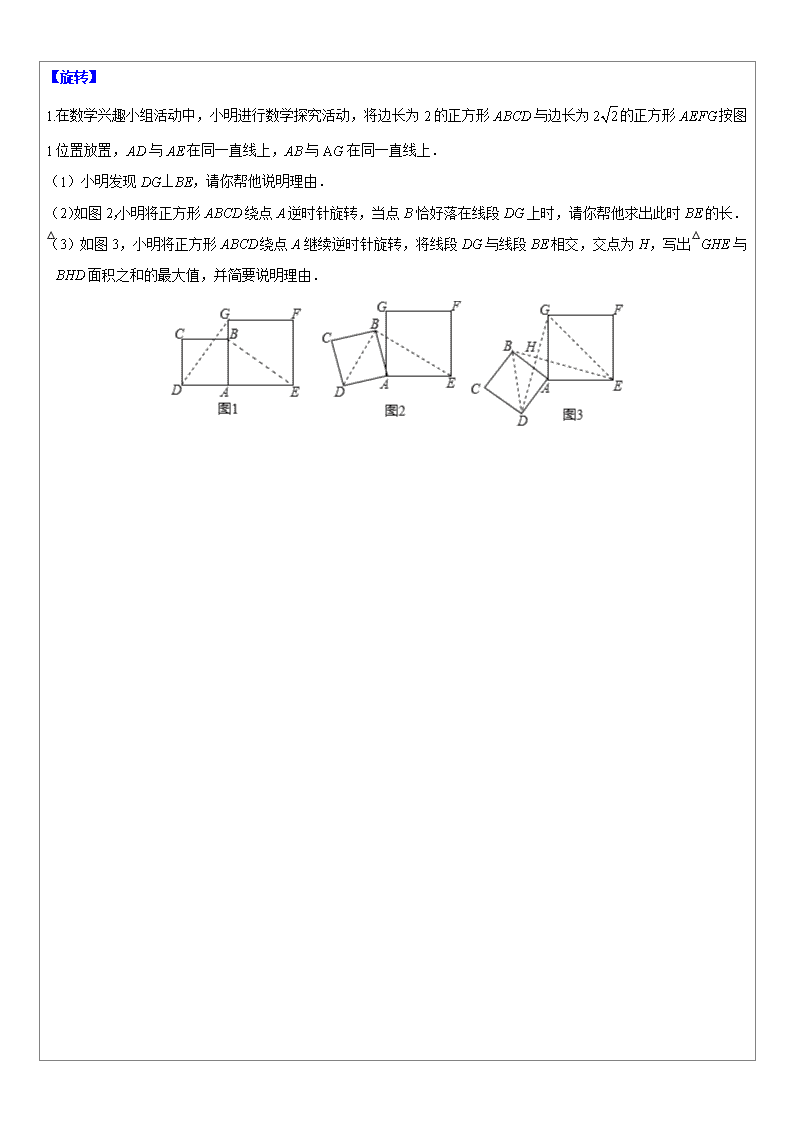‎ ‎2.如图，△ABC和△DBC是两个具有公共边的全等三角形，AB=AC=3cm，BC=2cm，将△DBC沿射线BC平移一定的距离得到△D1B1C1，连接AC1，BD1．如果四边形ABD1C1是矩形，那么平移的距离为 ▲ cm．‎ ‎【旋转】‎ ‎1.在数学兴趣小组活动中，小明进行数学探究活动，将边长为2的正方形ABCD与边长为的正方形AEFG按图1位置放置，AD与AE在同一直线上，AB与AG在同一直线上．‎ ‎（1）小明发现DG⊥BE，请你帮他说明理由．‎ ‎（2）如图2，小明将正方形ABCD绕点A逆时针旋转，当点B恰好落在线段DG上时，请你帮他求出此时BE的长．‎ ‎（3）如图3，小明将正方形ABCD绕点A继续逆时针旋转，将线段DG与线段BE相交，交点为H，写出△GHE与△BHD面积之和的最大值，并简要说明理由．‎ ‎2.如图，Rt△ABC中，∠C=90°，AB=15，BC=9，点P，Q分别在BC，AC上，CP=3x，CQ=4x（0＜x＜3）．把△PCQ绕点P旋转，得到△PDE，点D落在线段PQ上．‎ ‎（1）求证：PQ∥AB；‎ ‎（2）若点D在∠BAC的平分线上，求CP的长；‎ ‎（3）若△PDE与△ABC重叠部分图形的周长为T，且12≤T≤16，求x的取值范围．‎ ‎【作业】1.如图，在△ABC中，∠BAC=60°，∠ABC=90°，直线l1∥l2∥l3，l1与l2之间距离是1，l2与l3之间距离是2，且l1，l2，l3分别经过点A，B，C，则边AC的长为 ▲ ．‎ ‎2. 如图，过原点O的直线与反比例函数y1，y2的图象在第一象限内分别交于点A、B，且A为OB的中点，若函数，则y2与x的函数表达式是 ▲ ．‎ 答案：‎ ‎【轴对称】‎ ‎1.如图，Rt△ABC中，∠ACB＝90º，AC＝3，BC＝4，将边AC沿CE翻折，使点A落在AB上的点D处；再将边BC沿CF翻折，使点B落在CD的延长线上的点B′处，两条折痕与斜边AB分别交于点E、F，则线段B′F的长为【 】‎ A. B. C. D. ‎ ‎【答案】B．‎ ‎【考点】翻折变换（折叠问题）；折叠的性质；等腰直角三角形的判定和性质；勾股定理．‎ ‎【分析】根据折叠的性质可知，‎ ‎∴.‎ ‎∵，∴. ∴是等腰直角三角形. ∴.‎ ‎∴. ∴.‎ ‎∵，∴.‎ 在中，根据勾股定理，得AB=5，∴.∴.‎ 在中，根据勾股定理，得，∴.‎ ‎∴.‎ 在中，根据勾股定理，得.‎ 故选B．‎ ‎2.如图， 矩形中，AB=8，BC=6，P为AD上一点， 将△ABP 沿BP翻折至△EBP， PE与CD相交于点O，且OE=OD，则AP的长为 ▲ ．‎ ‎【答案】.‎ ‎【考点】翻折变换（折叠问题）；矩形的性质；折叠对称的性质；勾股定理，全等三角形的判定和性质；方程思想的应用. ‎ ‎【分析】如答图，∵四边形是矩形，‎ ‎∴.‎ 根据折叠对称的性质，得，‎ ‎∴.‎ 在和中，∵，‎ ‎∴≌.∴. ‎ ‎∴.‎ 设，则，∴.‎ 在中，根据勾股定理，得，即.解得.‎ ‎∴AP的长为.‎ ‎【平移】‎ ‎1. 若函数的图像如图所示，则关于的不等式的解集为【 】‎ A. B. C. D. ‎ ‎【答案】C.‎ ‎【考点】直线的平移；不等式的图象解法；数形结合思想的应用.‎ ‎【分析】如答图，将函数的图像向右平移3 个单位得到函数的图象，‎ 由图象可知，当时，函数的图象在轴上方，即.‎ ‎∴关于的不等式的解集为.‎ 故选C.‎ ‎2.如图，△ABC和△DBC是两个具有公共边的全等三角形，AB=AC=3cm，BC=2cm，将△DBC沿射线BC平移一定的距离得到△D1B1C1，连接AC1，BD1．如果四边形ABD1C1是矩形，那么平移的距离为 ▲ cm．‎ ‎【答案】7．‎ ‎【考点】面动平移问题；相似三角形的判定和性质；等腰三角形的性质；矩形的性质；平移的性质．‎ ‎【分析】如答图，过点A作AE⊥BC于点E，‎ ‎∵∠AEB=∠AEC1=90°，∴∠BAE+∠ABC=90°.‎ ‎∵AB=AC，BC=2，∴BE=CE=BC=1，‎ ‎∵四边形ABD1C1是矩形，∴∠BAC1=90°.‎ ‎∴∠ABC+∠AC1B=90°. ∴∠BAE=∠AC1B.‎ ‎∴△ABE∽△C1BA. ∴.‎ ‎∵AB=3，BE=1，∴.∴BC1=9.‎ ‎∴CC1=BC1﹣BC=9﹣2=7，即平移的距离为7．‎ ‎【旋转】‎ ‎1.在数学兴趣小组活动中，小明进行数学探究活动，将边长为2的正方形ABCD与边长为的正方形AEFG按图1位置放置，AD与AE在同一直线上，AB与AG在同一直线上．‎ ‎（1）小明发现DG⊥BE，请你帮他说明理由．‎ ‎（2）如图2，小明将正方形ABCD绕点A逆时针旋转，当点B恰好落在线段DG上时，请你帮他求出此时BE的长．‎ ‎（3）如图3，小明将正方形ABCD绕点A继续逆时针旋转，将线段DG与线段BE相交，交点为H，写出△GHE与△BHD面积之和的最大值，并简要说明理由．‎ ‎【答案】解：（1）∵四边形ABCD和四边形AEFG都为正方形，∴AD=AB，∠DAG=∠BAE=90°，AG=AE，‎ ‎∴△ADG≌△ABE（SAS）.∴∠AGD=∠AEB.‎ 如答图1，延长EB交DG于点H，‎ 在△ADG中，∵∠AGD+∠ADG=90°，‎ ‎∴∠AEB+∠ADG=90°.‎ 在△EDH中，∵∠AEB+∠ADG+∠DHE=180°，‎ ‎∴∠DHE=90°. ∴DG⊥BE.‎ ‎（2）∵四边形ABCD和四边形AEFG都为正方形，∴AD=AB，∠DAB=∠GAE=90°，AG=AE，‎ ‎∴∠DAB+∠BAG=∠GAE+∠BAG，即∠DAG=∠BAE，‎ ‎∴△ADG≌△ABE（SAS）.∴DG=BE.‎ 如答图2，过点A作AM⊥DG交DG于点M，则∠AMD=∠AMG=90°，‎ ‎∵BD为正方形ABCD的对角线，∴∠MDA=45°.‎ 在Rt△AMD中，∵∠MDA=45°，AD=2，‎ ‎∴.‎ 在Rt△AMG中，根据勾股定理得：，‎ ‎∵，∴.‎ ‎（3）△GHE和△BHD面积之和的最大值为6，理由如下：‎ ‎∵对于△EGH，点H在以EG为直径的圆上，∴当点H与点A重合时，△EGH的高最大；‎ ‎∵对于△BDH，点H在以BD为直径的圆上，∴当点H与点A重合时，△BDH的高最大.‎ ‎∴△GHE和△BHD面积之和的最大值为2+4=6．‎ ‎【考点】面动旋转问题；正方形的性质；全等三角形的判定和性质；三角形内角和定理；等腰直角三角形的性质，勾股定理；数形结合思想的应用．‎ ‎【分析】（1）由四边形ABCD与四边形AEFG为正方形，利用正方形的性质得到两对边相等，且夹角相等，利用SAS得到△ADG≌△ABE，利用全等三角形对应角相等得∠AGD=∠AEB，作辅助线“延长EB交DG于点H”，利用等角的余角相等得到∠DHE=90°，从而利用垂直的定义即可得DG⊥BE.‎ ‎（2）由四边形ABCD与四边形AEFG为正方形，利用正方形的性质得到两对边相等，且夹角相等，利用SAS得到△ADG≌△ABE，利用全等三角形对应边相等得到DG=BE，作辅助线“过点A作AM⊥DG交DG于点M”，则∠AMD=∠AMG=90°，在Rt△AMD中，根据等腰直角三角形的性质求出AM的长，即为DM的长，根据勾股定理求出GM的长，进而确定出DG的长，即为BE的长.‎ ‎（3）△GHE和△BHD面积之和的最大值为6，理由为：对两个三角形，点H分别在以EG为直径的圆上和以BD为直径的圆上，当点H与点A重合时，两个三角形的高最大，即可确定出面积的最大值．‎ ‎2.如图，Rt△ABC中，∠C=90°，AB=15，BC=9，点P，Q分别在BC，AC上，CP=3x，CQ=4x（0＜x＜3）．把△PCQ绕点P旋转，得到△PDE，点D落在线段PQ上．‎ ‎（1）求证：PQ∥AB；‎ ‎（2）若点D在∠BAC的平分线上，求CP的长；‎ ‎（3）若△PDE与△ABC重叠部分图形的周长为T，且12≤T≤16，求x的取值范围．‎ ‎【答案】解：（1）证明：∵在Rt△ABC中，AB=15，BC=9，‎ ‎∴．‎ ‎∵，∴．‎ 又∵∠C=∠C，∴△PQC∽△BAC. ∴∠CPQ=∠B. ∴PQ∥AB.‎ ‎（2）如答图1，连接AD，‎ ‎∵PQ∥AB，∴∠ADQ=∠DAB．‎ ‎∵点D在∠BAC的平分线上，∴∠DAQ=∠DAB.‎ ‎∴∠ADQ=∠DAQ. ∴AQ=DQ．‎ 在Rt△CPQ中，∵CP=3x，CQ=4x，∴PQ=5x.‎ ‎∵PD=PC=3x，∴DQ=2x．‎ ‎∵AQ=12﹣4x，∴12﹣4x=2x，解得x=2.‎ ‎∴CP=3x=6．‎ ‎（3）当点E在AB上时，‎ ‎∵PQ∥AB，∴∠DPE=∠PEB．‎ ‎∵∠CPQ=∠DPE，∠CPQ=∠B，∴∠B=∠PEB. ∴PB=PE=5x.‎ ‎∴3x+5x=9，解得．‎ ‎①当0＜x≤时，，此时0＜T≤.‎ ‎∴当0＜x≤时，T随x的增大而增大，‎ ‎∵12≤T≤16，∴当12≤T≤时，1≤x≤.‎ ‎②当＜x＜3时，‎ 如答图2，设PE交AB于点G，DE交AB于F，作GH⊥FQ，垂足为H，‎ ‎∴HG=DF，FG=DH，Rt△PHG∽Rt△PDE.‎ ‎∴．‎ ‎∵PG=PB=9﹣3x，∴.‎ ‎∴.‎ ‎∴，‎ ‎∴，‎ 此时，＜T＜18．‎ ‎∴当＜x＜3时，T随x的增大而增大.‎ ‎∵12≤T≤16，∴当＜T≤16时，＜x≤.‎ 综上所述，当12≤T≤16时，x的取值范围是1≤x≤．‎ ‎【考点】面动旋转问题；勾股定理；相似三角形的判定和性质；平行的判定和性质；方程思想、函数思想、分类思想的应用．‎ ‎【分析】（1）先根据勾股定理求出AC的长，再由相似三角形的判定定理得出△PQC∽△BAC，由相似三角形的性质得出∠CPQ=∠B，由此可得出结论.‎ ‎（2）连接AD，根据PQ∥AB可知∠ADQ=∠DAB，再由点D在∠BAC的平分线上，得出∠DAQ=∠DAB，故∠ADQ=∠DAQ，AQ=DQ．在Rt△CPQ中根据勾股定理可知，AQ=12﹣4x，故可得出x的值，进而得出结论.‎ ‎（3）当点E在AB上时，根据等腰三角形的性质求出x的值，再分0＜x≤；＜x＜3两种情况进行分类讨论．‎ 作业：‎ ‎1.如图，在△ABC中，∠BAC=60°，∠ABC=90°，直线l1∥l2∥l3，l1与l2之间距离是1，l2与l3之间距离是2，且l1，l2，l3分别经过点A，B，C，则边AC的长为 ▲ ．‎ ‎【答案】.‎ ‎【考点】平行线的性质；锐角三角函数定义；特殊角的三角函数值；相似三角形的判定和性质；勾股定理．‎ ‎【分析】如答图，过点B作EF⊥l2，交l1于E，交l3于F， ‎ ‎ ∵∠BAC=60°，∠ABC=90°，∴．‎ ‎∵直线l1∥l2∥l3，∴EF⊥l1，EF⊥l3. ∴∠AEB=∠BFC=90°．[来源:学|科|网]‎ ‎∵∠ABC=90°，∴∠EAB=90°﹣∠ABE=∠FBC.‎ ‎∴△BFC∽△AEB，∴．‎ ‎∵EB=1，∴FC=．‎ 在Rt△BFC中，．‎ 在Rt△ABC中， ．‎ ‎2. 如图，过原点O的直线与反比例函数y1，y2的图象在第一象限内分别交于点A、B，且A为OB的中点，若函数，则y2与x的函数表达式是 ▲ ．‎ ‎【答案】.‎ ‎【考点】反比例函数的图象和性质；曲线上点的坐标与方程的关系；待定系数法的应用.‎ ‎【分析】设y2与x的函数表达式是，‎ ‎∵点B在反比例函数y2的图象上，∴可设. ‎ ‎∵A为OB的中点，∴.‎ ‎∵点A在反比例函数的图象上，∴，解得.‎ ‎∴y2与x的函数表达式是.‎