盐城2008年高中阶段教育招生统一考试数学试题 7页

盐城二○○八年高中阶段教育招生统一考试 数学试题 注 意 事 项：‎ 考生在答题前请认真阅读注意事项及各题答题要求 ‎1．本试卷共8页，包含选择题（第1题~第10题，共10题，计30分），非选择题（第11题~第28题，共18题，计120分）两部分．本次考试时间为120分钟，满分为150分．考试形式为闭卷．考试结束后，请将本试卷和答题卡一并交回．‎ ‎2．答题前，请你务必将自己的姓名、准考证号用书写黑色字迹的0.5毫米签字笔填写在试卷及答题卡．‎ ‎3．请认真核对监考老师所粘贴的条形码上的姓名、准考证号是否与你本人的相符．‎ ‎4．作答非选择题必须用书写黑色字迹的0.5毫米签字笔写在答题卡上的指定位置，在其它位置作答一律无效．作答选择题必须用2B铅笔把答题卡上对应选项的方框涂满涂黑．如需改动，请用橡皮擦干净后，再选涂其它答案．‎ ‎5．如有作图需要，可用2B铅笔作答，并用签字笔加黑描写清楚．‎ 一、选择题：本大题共10小题，每小题3分，计30分．‎ 1．的立方是（ ）‎ A． B． C． D．‎ ‎2．下列运算正确的是（ ）‎ A． B． C． D．‎ 3．2008年北京奥运会圣火在全球传递的里程约为‎137000km，用科学记数法表示为（ ）‎ A．km B．km C．km D．km ‎4．下列四个几何体中，主视图、左视图、俯视图完全相同的是（ ）‎ a ‎0‎ ‎1‎ 第5题图 A．圆锥 B．球 C．圆柱 D．三棱柱 5．实数在数轴上对应的点如图所示，则，，的大小 关系正确的是（ ）‎ A． B． C． D．‎ ‎6．用计算器求2008的算术平方根时，下列四个键中，必须按的键是（ ）‎ A．sin B．cos C． D．‎ 7．已知如图1所示的四张牌，若将其中一张牌旋转后得到图2，则旋转的牌是（ ）‎ 图1‎ 图2‎ A．‎ B．‎ C．‎ D．‎ ‎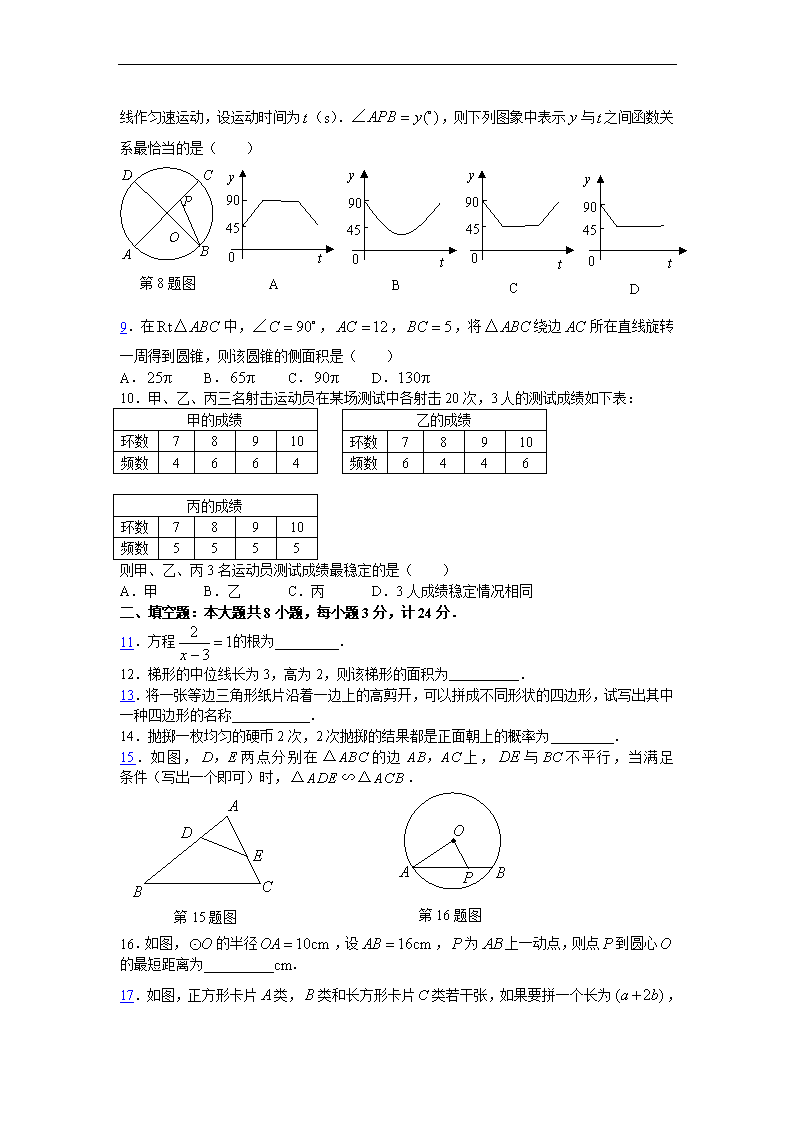8．如图，为的四等分点，动点从圆心出发，沿 路线作匀速运动，设运动时间为（s）．，则下列图象中表示与之间函数关系最恰当的是（ ）‎ 第8题图 A B C D O P B．‎ t y ‎0‎ ‎45‎ ‎90‎ D．‎ t y ‎0‎ ‎45‎ ‎90‎ A．‎ t y ‎0‎ ‎45‎ ‎90‎ C．‎ t y ‎0‎ ‎45‎ ‎90‎ 9．在中，，，，将绕边所在直线旋转一周得到圆锥，则该圆锥的侧面积是（ ）‎ A． B． C． D．‎ ‎10．甲、乙、丙三名射击运动员在某场测试中各射击20次，3人的测试成绩如下表：‎ 甲的成绩 环数 ‎7‎ ‎8‎ ‎9‎ ‎10‎ 频数 ‎4‎ ‎6‎ ‎6‎ ‎4‎ 乙的成绩 环数 ‎7‎ ‎8‎ ‎9‎ ‎10‎ 频数 ‎6‎ ‎4‎ ‎4‎ ‎6‎ 丙的成绩 环数 ‎7‎ ‎8‎ ‎9‎ ‎10‎ 频数 ‎5‎ ‎5‎ ‎5‎ ‎5‎ 则甲、乙、丙3名运动员测试成绩最稳定的是（ ）‎ A．甲 B．乙 C．丙 D．3人成绩稳定情况相同 二、填空题：本大题共8小题，每小题3分，计24分．‎ 11．方程的根为 ．‎ ‎12．梯形的中位线长为3，高为2，则该梯形的面积为 ．‎ 13．将一张等边三角形纸片沿着一边上的高剪开，可以拼成不同形状的四边形，试写出其中一种四边形的名称 ．‎ ‎14．抛掷一枚均匀的硬币2次，2次抛掷的结果都是正面朝上的概率为 ．‎ 15．如图，两点分别在的边上，与不平行，当满足 条件（写出一个即可）时，．‎ 第16题图 第15题图 ‎16．如图，的半径，设，为上一动点，则点到圆心的最短距离为 cm．‎ 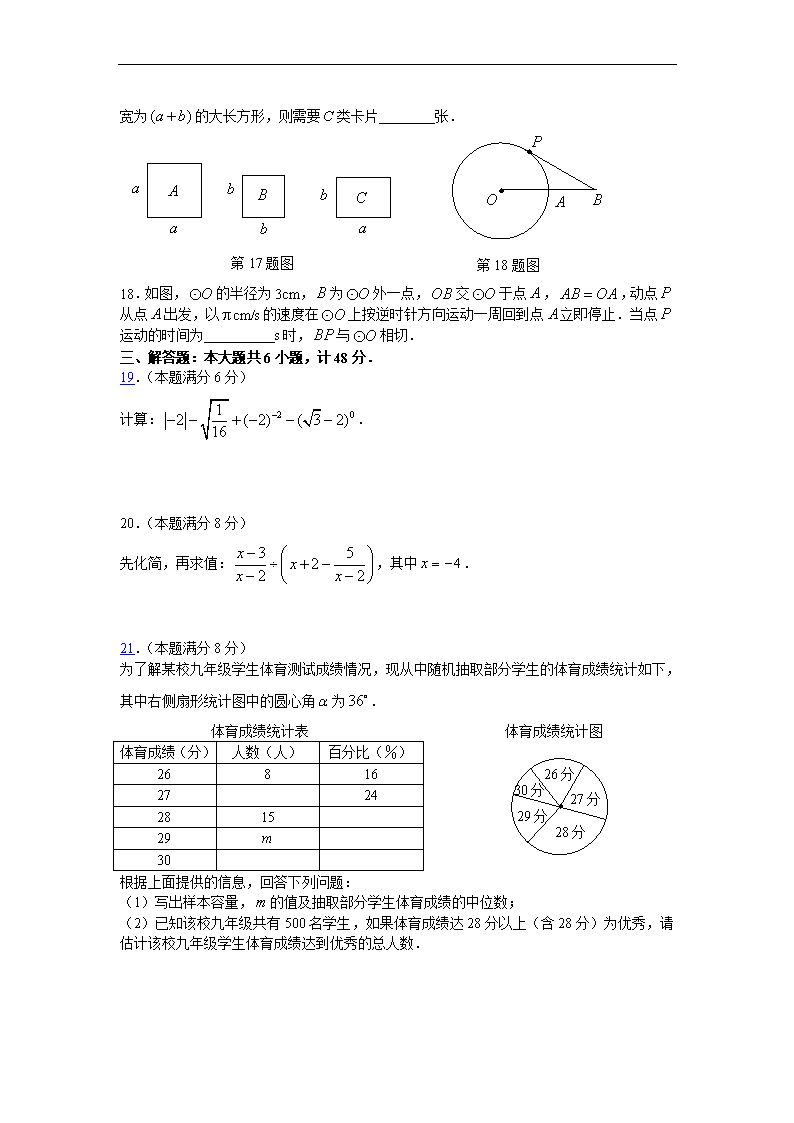17．如图，正方形卡片类，类和长方形卡片类若干张，如果要拼一个长为 ‎，宽为的大长方形，则需要类卡片 张．‎ 第18题图 第17题图 ‎18．如图，的半径为3cm，为外一点，交于点，，动点从点出发，以cm/s的速度在上按逆时针方向运动一周回到点立即停止．当点运动的时间为 s时，与相切．‎ 三、解答题：本大题共6小题，计48分．‎ 19．（本题满分6分）‎ 计算：．‎ ‎20．（本题满分8分）‎ 先化简，再求值：，其中．‎ 21．（本题满分8分）‎ 为了解某校九年级学生体育测试成绩情况，现从中随机抽取部分学生的体育成绩统计如下，其中右侧扇形统计图中的圆心角为．‎ 体育成绩统计表 体育成绩统计图 体育成绩（分）‎ 人数（人）‎ ‎30分 ‎26分 ‎27分 ‎28分 ‎29分 百分比（％）‎ ‎26‎ ‎8‎ ‎16‎ ‎27‎ ‎24‎ ‎28‎ ‎15‎ ‎29‎ m ‎30‎ 根据上面提供的信息，回答下列问题：‎ ‎（1）写出样本容量，的值及抽取部分学生体育成绩的中位数；‎ ‎（2）已知该校九年级共有500名学生，如果体育成绩达28分以上（含28分）为优秀，请估计该校九年级学生体育成绩达到优秀的总人数．‎ ‎22．（本题满分8分）‎ 如图，在的正方形网格中，的顶点分别为，，．‎ ‎（1）以点为位似中心，按比例尺的位似中心的同侧将放大为，放大后点的对应点分别为，画出，并写出点的坐标；‎ ‎（2）在（1）中，若为线段上任一点，写出变化后点的对应点的坐标．‎ x y 第22题图 23．（本题满分8分）‎ 某工厂接受一批支援四川省汶川灾区抗震救灾帐篷的生产任务．根据要求，帐篷的一个横截面框架由等腰三角形和矩形组成（如图所示）．已知等腰的底角，且，矩形的边，这个横截面框架（包括）所用的钢管总长为15m，求帐篷的篷顶到底部的距离．（结果精确到0.1m）‎ 第23题图 ‎24．（本题满分10分）‎ 一只不透明的袋子中装有4个小球，分别标有数字2，3，4，，这些球除数字外都相同．甲、乙两人每次同时从袋中各随机摸出1个球，并计算摸出的这2个小球上数字之和．记录后都将小球放回袋中搅匀，进行重复实验．实验数据如下表：‎ 摸球总次数 ‎10‎ ‎20‎ ‎30‎ ‎60‎ ‎90‎ ‎120‎ ‎180‎ ‎240‎ ‎330‎ ‎450‎ ‎“和为7”出现的频数 ‎1‎ ‎9‎ ‎14‎ ‎24‎ ‎26‎ ‎37‎ ‎58‎ ‎82‎ ‎109‎ ‎150‎ ‎0.10‎ ‎0.45‎ ‎0.47‎ ‎0.40‎ ‎0.29‎ ‎0.31‎ ‎0.32‎ ‎0.34‎ ‎0.33‎ ‎0.33‎ ‎“和为7”出现的频率 解答下列问题：‎ ‎（1）如果实验继续进行下去，根据上表数据，出现“和为7”的概率将稳定在它的概率附近，试估计出现“和为7”的概率；‎ ‎（2）根据（1），若是不等于2，3，4的自然数，试求的值．‎ 四、解答题：本大题共4小题，计48分．‎ 25．（本题满分12分）‎ 在购买某场足球赛门票时，设购买门票数为（张），总费用为（元）．现有两种购买方案：‎ 方案一：若单位赞助广告费10000元，则该单位所购门票的价格为每张60元；‎ ‎（总费用=广告赞助费+门票费）‎ 方案二：购买门票方式如图所示．‎ 解答下列问题：‎ ‎（1）方案一中，与的函数关系式为 ；‎ 方案二中，当时，与的函数关系式为 ；‎ 当时，与的函数关系式为 ；‎ ‎（2）如果购买本场足球赛超过100张，你将选择哪一种方案，使总费用最省？请说明理由；‎ ‎（3）甲、乙两单位分别采用方案一、方案二购买本场足球赛门票共700张，花去总费用计58000元，求甲、乙两单位各购买门票多少张．‎ 第25题图 y（元）‎ x（张）‎ ‎100‎ ‎150‎ ‎14000‎ ‎10000‎ O 26．（本题满分12分）‎ 阅读理解：对于任意正实数，，，‎ ‎，只有点时，等号成立．‎ 结论：在（均为正实数）中，若为定值，则，‎ 只有当时，有最小值．‎ 根据上述内容，回答下列问题：‎ 若，只有当 时，有最小值 ．‎ 思考验证：如图1，为半圆的直径，为半圆上任意一点，（与点不重合）．过点作，垂足为，，．‎ A O D B C 第26题图1‎ 试根据图形验证，并指出等号成立时的条件．‎ y x B A D P C O 第26题图2‎ 探索应用：如图2，已知，为双曲线上的任意一点，过点作轴于点，轴于点．求四边形面积的最小值，并说明此时四边形的形状．‎ 27．（本小题满分12分）‎ 如图，直线经过点，且与轴交于点，将抛物线沿轴作左右平移，记平移后的抛物线为，其顶点为．‎ ‎（1）求的度数；‎ ‎（2）抛物线与轴交于点，与直线交于两点，其中一个交点为，当线段轴时，求平移后的抛物线对应的函数关系式；‎ ‎（3）在抛物线平移过程中，将沿直线翻折得到，点能否落在抛物线上？如能，求出此时抛物线顶点的坐标；如不能，说明理由．‎ 第27题图 A O B y x 备用图 A O B y x 28．（本题满分12分）‎ 如图甲，在中，为锐角，点为射线上一点，连接，以为一边且在的右侧作正方形．‎ 解答下列问题：‎ ‎（1）如果，，‎ ‎①当点在线段上时（与点不重合），如图乙，线段之间的位置关系为 ，数量关系为 ．‎ ‎②当点在线段的延长线时，如图丙，①中的结论是否仍然成立，为什么？‎ 图甲 A B D F E C 图乙 A B D E C F 第28题图 图丙 A B D C E ‎（2）如果，，点在线段上运动．‎ 试探究：当满足一个什么条件时，（点重合除外）？画出相应图形，并说明理由．（画图不写作法）‎ ‎（3）若，，在（2）的条件下，设正方形的边与线段相交于点，求线段长的最大值．‎