初三中考数学复习二次函数复习导学案无答案 7页

个 性 化 辅 导 教 案 科 目 ‎ 数学 ‎ 授课老师 学生姓名 年 级 课 题 教学目标 重 点 ‎ 重点掌握二次函数定义、解析式、图象及其性质 难 点 难点是配方法求顶点坐标，只要坚持配完后看看与原二次函数是否相等即可 教学过程（内容）：‎ ‎1. 掌握二次函数的概念，形如的函数，叫做二次函数，定义域。‎ ‎ 特别地，时，是二次函数特例。‎ ‎ 2. 能由实际问题确定函数解析式和自变量取值范围，明确它有三个待定系数a，b，c，，需三个相等关系，才可解。‎ ‎ 3. 二次函数解析式有三种：‎ ‎ （1） 一般式 ‎ （2） 顶点式； 顶点 ‎ （3） 双根式；是图象与x轴交点坐标。‎ ‎ 4. 二次函数图象：抛物线 ‎ 分布象限，可能在两个象限（1），三个象限（2），四个象限（3）。‎ ‎ 5. 抛物线与抛物线形状、大小相同，只有位置不同。‎ ‎ 6. 描点法画抛物线了解开口、顶点、对称轴、最值。‎ ‎ （1）a决定开口：‎ ‎ 开口向上，开口向下。‎ ‎ 表示开口宽窄，越大开口越窄。‎ ‎ （2）顶点，当时，y有最值为。‎ ‎ （3）对称轴 ‎ （4）与y轴交点（0，c），有且仅有一个 ‎ （5）与x轴交点A（），B（），令则。‎ ‎ ①△＞0，有，两交点A、B。‎ ‎ ②△＝0，有，一个交点。‎ ‎ ③△＜0，没有实数与x轴无交点。‎ ‎ 7. 配方可得 ‎ 向右（）或向左（）平移个单位，得到，再向上向下平移个单位，便得，即 。‎ ‎ 8. 五点法作抛物线 ‎ （1）找顶点，画对称轴。‎ ‎ （2）找图象上关于直线对称的四个点（如与坐标轴的交点等）。‎ ‎ （3）把上述五个点连成光滑曲线。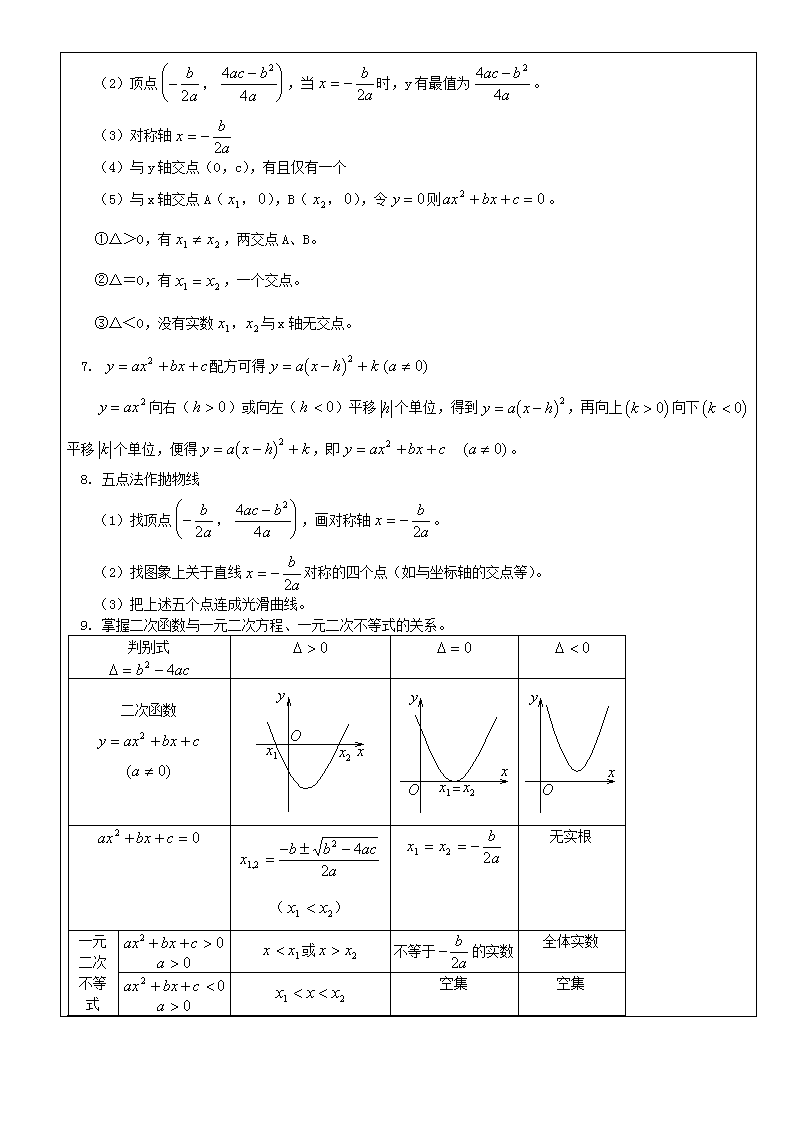‎ ‎ 9. 掌握二次函数与一元二次方程、一元二次不等式的关系。‎ 判别式 二次函数 ‎（）‎ 无实根 一元 二次 或 不等于的实数 全体实数 不等 式 空集 空集 数学讲义 课堂检测 听课及知识掌握情况反馈：‎ 教学需：加快□ 保持□ 放慢□ 增加内容□‎ 教师课后 赏识评价 学生课后 自我评价 例1. 已知抛物线，五点法作图。‎ ‎ 解：‎ ‎ ∴此抛物线的顶点为 ‎ ∴对称轴为 ‎ 令，即解方程 ‎ ∴抛物线与x轴交于点A（1，0），B（5，0）‎ ‎ 令则，得抛物线与y轴交于点C（0，）‎ ‎ 又C（0，）关于对称轴的对称点为D ‎ 将C、A、M、B、D五点连成光滑曲线，此即为抛物线的草图。‎ ‎ 例2. 已知抛物线如图，试确定：‎ ‎ （1）及的符号；‎ ‎ （2）与的符号。‎ ‎ 解：（1）由图象知抛物线开口向下，对称轴在y轴左侧，过A（1，0）与y轴交于B（0，c），在x轴上方 ‎ ∵抛物线与x轴有两交点 ‎ （2）∵抛物线过A（1，0）‎ ‎ 例3. 求二次函数解析式：‎ ‎ （1）抛物线过（0，2），（1，1），（3，5）；‎ ‎ （2）顶点M（-1，2），且过N（2，1）；‎ ‎ （3）与x轴交于A（-1，0），B（2，0），并经过点M（1，2）。‎ ‎ 解：（1）设二次函数解析式为 ‎ 由题意 ‎ ‎ ∴所求二次函数为 ‎ （2）设二次函数解析式为 ‎ ∵顶点M（-1，2）‎ ‎ ∵抛物线过点N（2，1）‎ ‎ ∴所求解析式 ‎ 即 ‎ （3）设二次函数解析式为 ‎ ∵抛物线与x轴交于A（-1，0），B（2，0）‎ ‎ ∵抛物线过M（1，2）‎ ‎ ∴所求解析式 ‎ 即 ‎ 例4. 已知二次函数在时，y取最大值，且抛物线与直线相交，试写出二次函数的解析式，并求出抛物线与直线的交点坐标。‎ ‎ 解：∵二次函数有最大值 ‎ 即 ‎ ∴抛物线为 ‎ 由题意 ‎ ∴抛物线与直线的交点坐标是与 ‎ 例5. 已知函数，它的顶点为（-3，-2），与交于点（1，6），求的解析式。‎ ‎ 解：二次函数的解析式可化为：‎ ‎ ∵已知顶点为，可得：‎ ‎ 又点（1，6）在抛物线上，得：‎ ‎ 由<1>、<2>、<3>可解得：‎ ‎ 又点（1，6）在直线上 ‎ 例6. 抛物线过（-1，-1）点，它的对称轴是直线，且在x轴上截取长度为的线段，求解析式。‎ ‎ 解：∵对称轴为，即 ‎ ∴可设二次函数解析式为 ‎ ∵在x轴上截取长度为 ‎ ∴抛物线过与两点 ‎ 又∵（-1，-1）在抛物线上 ‎ 由<1>、<2>解得：‎ ‎ ∴解析式为 ‎ 即 ‎（答题时间：35分钟）‎ 一. 选择题。‎ ‎ 1. 用配方法将化成的形式（ ）‎ ‎ A. B. ‎ ‎ C. D. ‎ ‎ 2. 对于函数，下面说法正确的是（ ）‎ ‎ A. 在定义域内，y随x增大而增大 ‎ B. 在定义域内，y随x增大而减小 ‎ C. 在内，y随x增大而增大 ‎ D. 在内，y随x增大而增大 ‎ 3. 已知，那么的图象（ ）‎ ‎ 4. 已知点（-1，3）（3，3）在抛物线上，则抛物线的对称轴是（ ）‎ ‎ A. B. C. D. ‎ ‎ 5. 一次函数和二次函数在同一坐标系内的图象（ ）‎ ‎ 6. 函数的最大值为（ ）‎ ‎ A. B. C. D. 不存在 二. 填空题。‎ ‎ 7. 是二次函数，则____________。‎ ‎ 8. 抛物线的开口向____________，对称轴是____________，顶点坐标是____________。‎ ‎ 9. 抛物线的顶点是（2，3），且过点（3，1），则___________，____________，____________。‎ ‎ 10. 函数图象沿y轴向下平移2个单位，再沿x轴向右平移3个单位，得到函数____________的图象。‎ 三. 解答题。‎ ‎ 12. 抛物线，m为非负整数，它的图象与x轴交于A和B，A在原点左边，B在原点右边。‎ ‎ （1）求这个抛物线解析式。‎ ‎ （2）一次函数的图象过A点与这个抛物线交于C，且，求一次函数解析式。‎ ‎[参考答案]‎ 一. 选择题。‎ ‎ 1. A 2. C 3. C 4. D 5. C 6. C 二. 填空题。‎ ‎ 7. 1‎ ‎ 8. 下；；‎ ‎ 9. ‎ ‎ 10. 大，1‎ ‎ 11. ‎ 三. 解答题。‎ ‎ 12. （1）‎ ‎ 又∵m为非负整数 ‎ ∴抛物线为 ‎ （2）又A（-1，0），B（3，0）‎ ‎ 设C点纵坐标为a ‎ 当时，方程无解 ‎ 当时，方程