中考数学专题复习动态几何问题 4页

中考数学专题复习 动态几何问题 § 题型分类：点动型、线动型、面动型 § 运动形式：平移、旋转、翻折、滚动 题型一：点动型 点动型就是在三角形、矩形、梯形等一些几何图形上，设计一个或几个动点，并对这些点在运动变化的过程中产生的等量关系、变量关系、图形的特殊状态、图形间的特殊关系等进行研究。‎ ‎1、单动点型 例1．(08宁夏)如图，在边长为4的正方形中，点在上从向运动，连接交于点．‎ ‎（1）试证明：无论点运动到上何处时，都有△≌△；‎ ‎（2）当点在上运动到什么位置时，△的面积是正方形面积的；‎ ‎（3）若点从点运动到点，再继续在上运动到点，在整个运动过程中，当点 运动到什么位置时，△恰为等腰三角形．‎ 例2（2008湖北咸宁）如图，在△ABC 中，点O是AC边上的一个动点，过点O作直线MN∥BC，设MN交∠BCA的角平分线于点E，交∠BCA的外角平分线于点F．‎ ‎（1）求证：EO=FO；‎ ‎（2）当点O运动到何处时，四边形AECF是矩形？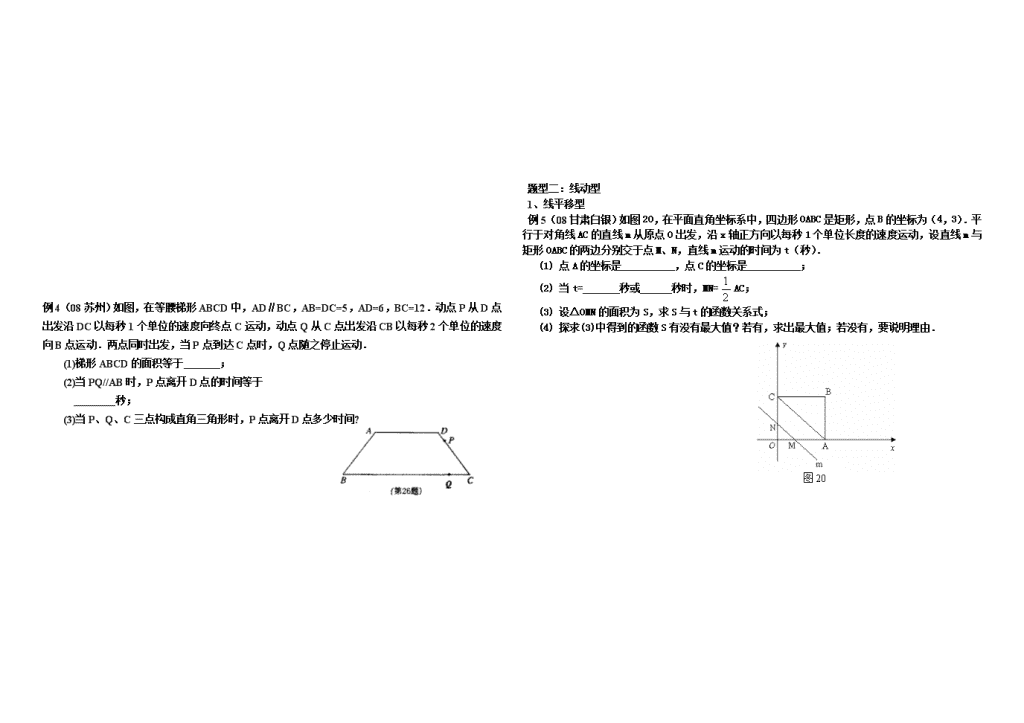‎ ‎ 并证明你的结论．‎ ‎2、双动点型 例3（08湖北咸宁）如图①，正方形 ABCD中，点A、B的坐标分别为（0，10），（8，4），点C在第一象限．动点P在正方形 ABCD的边上，从点A出发沿A→B→C→D匀速运动，同时动点Q以相同速度在x轴上运动，当P点到D点时，两点同时停止运动，设运动的时间为t秒．‎ (1) 当P点在边AB上运动时，点Q的横坐标（长度单位）关于运动时间t（秒）的函数图象如图②所示，请写出点Q开始运动时的坐标及点P运动速度；‎ ‎(2) 求正方形边长及顶点C的坐标；‎ ‎(第24题图①)‎ ‎（第24题图②）‎ ‎(3) 在(1)中当t为何值时，△OPQ的面积最大，并求此时P点的坐标．‎ 例4（08苏州）如图，在等腰梯形ABCD中，AD∥BC，AB=DC=5，AD=6，BC=12．动点P从D点 出发沿DC以每秒1个单位的速度向终点C运动，动点Q从C点出发沿CB以每秒2个单位的速度向B点运动．两点同时出发，当P点到达C点时，Q点随之停止运动．‎ ‎(1)梯形ABCD的面积等于 ； ‎ ‎(2)当PQ//AB时，P点离开D点的时间等于 ‎ 秒；‎ ‎(3)当P、Q、C三点构成直角三角形时，P点离开D点多少时间?‎ 题型二：线动型 ‎1、线平移型 例5（08甘肃白银）如图20，在平面直角坐标系中，四边形OABC是矩形，点B的坐标为（4，3）．平行于对角线AC的直线m从原点O出发，沿x轴正方向以每秒1个单位长度的速度运动，设直线m与矩形OABC的两边分别交于点M、N，直线m运动的时间为t（秒）．‎ ‎(1) 点A的坐标是__________，点C的坐标是__________；‎ ‎ (2) 当t= 秒或 秒时，MN=AC；‎ ‎(3) 设△OMN的面积为S，求S与t的函数关系式；‎ ‎(4) 探求(3)中得到的函数S有没有最大值？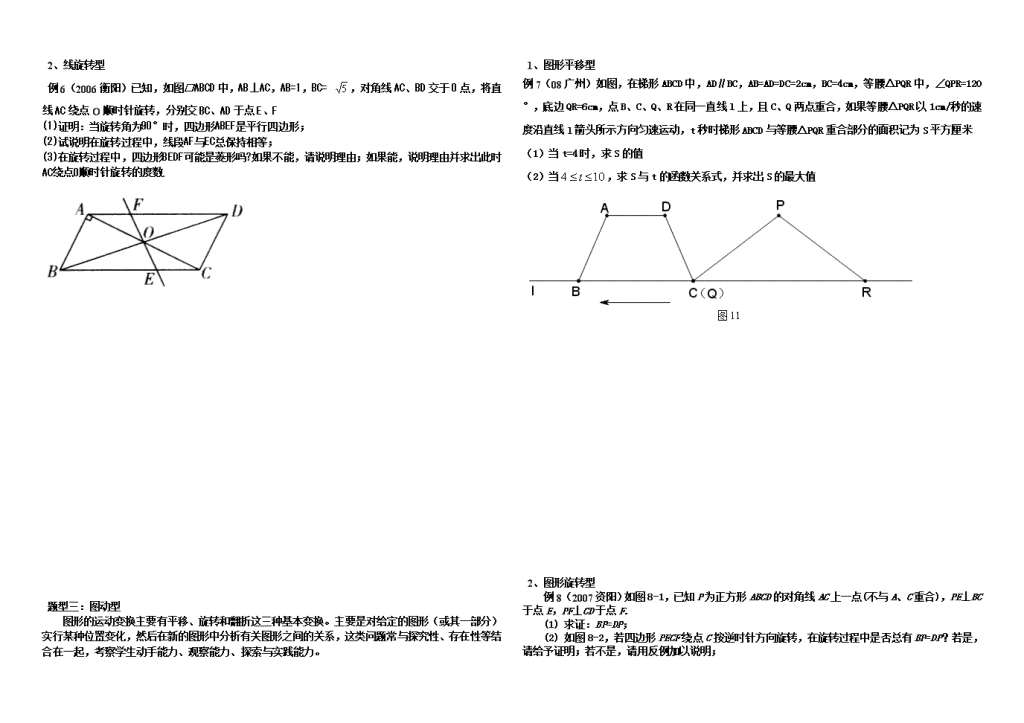若有，求出最大值；若没有，要说明理由．‎ 图20‎ ‎2、线旋转型 例6（2006衡阳）已知，如图□ABCD中，AB⊥AC，AB=1，BC= ，对角线AC、BD交于0点，将直线AC绕点O顺时针旋转，分别交BC、AD于点E、F ‎(1)证明：当旋转角为90°时，四边形ABEF是平行四边形；‎ ‎(2)试说明在旋转过程中，线段AF与EC总保持相等；‎ ‎(3)在旋转过程中，四边形BEDF可能是菱形吗?如果不能，请说明理由；如果能，说明理由并求出此时AC绕点0顺时针旋转的度数.‎ 题型三：图动型 图形的运动变换主要有平移、旋转和翻折这三种基本变换。主要是对给定的图形（或其一部分）实行某种位置变化，然后在新的图形中分析有关图形之间的关系，这类问题常与探究性、存在性等结合在一起，考察学生动手能力、观察能力、探索与实践能力。‎ ‎1、图形平移型 例7（08广州）如图，在梯形ABCD中，AD∥BC，AB=AD=DC=‎2cm，BC=‎4cm，等腰△PQR中，∠QPR=120°，底边QR=‎6cm，点B、C、Q、R在同一直线l上，且C、Q两点重合，如果等腰△PQR以‎1cm/秒的速度沿直线l箭头所示方向匀速运动，t秒时梯形ABCD与等腰△PQR重合部分的面积记为S平方厘米 ‎（1）当t=4时，求S的值 ‎（2）当，求S与t的函数关系式，并求出S的最大值 图11‎ ‎2、图形旋转型 例8（2007资阳）如图8-1，已知P为正方形ABCD的对角线AC上一点(不与A、C重合)，PE⊥BC于点E，PF⊥CD于点F.‎ ‎(1) 求证：BP=DP；‎ ‎(2) 如图8-2，若四边形PECF绕点C按逆时针方向旋转，在旋转过程中是否总有BP=DP？若是，请给予证明；若不是，请用反例加以说明；‎ ‎(3) 试选取正方形ABCD的两个顶点，分别与四边形PECF的两个顶点连结，使得到的两条线段在四边形PECF绕点C按逆时针方向旋转的过程中长度始终相等，并证明你的结论 .‎ 图8-2‎ 图8-1‎ ‎3、图形翻折型 例9（2007济宁）．如图，先把一矩形ABCD纸片对折，设折痕为MN，再把B点叠在折痕线上，得到△ABE。过B点折纸片使D点叠在直线AD上，得折痕PQ。‎ ‎(1)求证：△PBE∽△QAB；‎ ‎(2)你认为△PBE和△BAE相似吗？如果相似给出证明，如补相似请说明理由；‎ A ‎(第23题图)‎ D C B N M A D C B Q E P N ‎(3)如果直线EB折叠纸片，点A是否能叠在直线EC上？为什么？‎ ‎4、图形滚动 例10（2006临沂）如图，小正六边形沿着大正六边形的边缘顺时针滚动，小正六边形的边长是大正六边形边长的一半，当小正六边形由图①位置滚动到图②位置时，线段OA绕点O顺时针转过的角度为　 度。‎ 例11（2008年泰安市）（第19题）‎ 如图，将边长为1的正三角形沿轴正方向连续翻转2008次，点依次落在点的位置，则点的横坐标为 ．‎ y P1‎ A O x ‎（第19题）‎ P