H112017广东实验中考总复习数学专题4——三角形6页答案8已变尾注 8页

H11 2017广东中考专题（四）‎ ‎——三角形（6页，答案8）‎ 一、选择题（本题共10题，每小题3分，共30分）‎ ‎1．如图，直线a∥b，∠1=75°，∠2=35°，则∠3的度数是( ‎ 答案：C；‎ )‎ A． 75° B． 55° C． 40° D． 35° ‎ ‎2．如图，在△ABC中，AB=AD=DC，B=70°，则C的度数为（ ‎ 答案：A；‎ ）‎ A． 35° B．40° 　C．45° D． 50° ‎ ‎3．小明沿着与地面成30º的坡面向下走了2米，那么他下降（‎ 答案：A；‎     ）‎ A．1米 B．米 C．2米 D．米 ‎ ‎4．在正方形网格中，的位置如图所示，则的值为 （   ‎ 答案：A；‎  ）‎ A． B． C． D． ‎ ‎5．已知Rt△ABC中，∠C=90°，tanA= ， BC=8，则AC等于( ‎ 答案：A；‎ )‎ A．6 B． C．10 D．12‎ ‎6．如图，AB是⊙O的弦，AC是⊙O的切线，A为切点，BC经过圆心．若∠B=20°，则∠C的大小等于( ‎ 答案：D；‎ ) A． 20° B． 25° C． 40 D． 50°‎ ‎7．已知2是关于的方程的一个根，并且这个方程的两个根恰好是等腰三角形ABC的两条边长，则三角形ABC的周长为( ‎ 答案：B；‎ )‎ A． 10 B． 14 C． 10或14 D． 8或10‎ ‎8．下列四个三角形，与右图中的三角形相似的是（  ‎ 答案：B；‎  ）  ‎ ‎9．如图，点P在△ABC的边AC上，要判断△ABP∽△ACB，添加一个条件，不正确的是（　‎ 答案：D；‎ 　） A．∠ABP=∠C B．∠APB=∠ABC C．AP:AB=AB:AC D．AB:BP=AC:CB ‎10．如图，已知正△ABC的边长为2，E，F，G分别是AB，BC，CA上的点，且AE=BF=CG，设△EFG的面积为y，AE的长为x，则y关于x的函数图象大致是( ‎ 答案：D；‎ ) ‎ A． B． C． D．‎ ‎ ‎ 二、填空题（本题共6题，每小题4分，共24分）‎ ‎11．如图，在等腰三角形ABC中，AB=AC，DE垂直平分AB，已知∠ADE=40°，则∠DBC= ‎ 答案：15；‎ °． ‎ ‎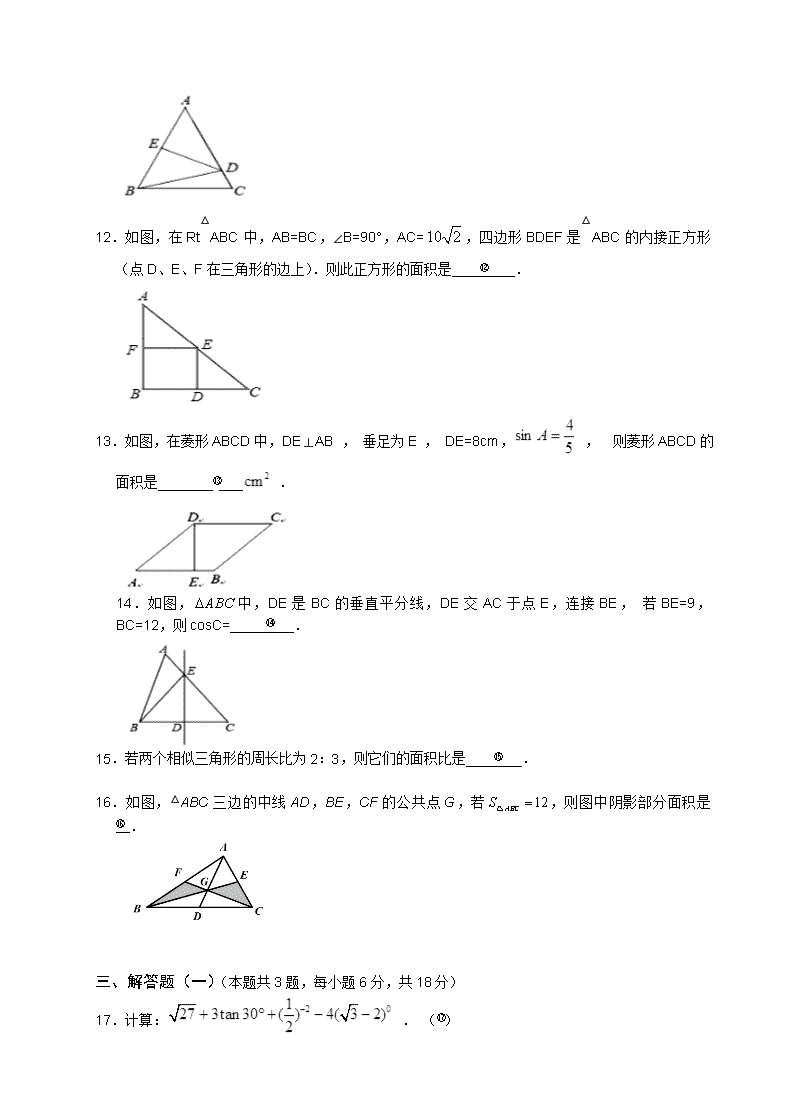12．如图，在Rt△ABC中，AB=BC，∠B=90°，AC=，四边形BDEF是△ABC的内接正方形（点D、E、F在三角形的边上）．则此正方形的面积是 ‎ 答案：25；‎ ． ‎ ‎13．如图，在菱形ABCD中，DE⊥AB ， 垂足为E ， DE=8cm， ， 则菱形ABCD的面积是_______‎ 答案：80；‎ ___ ． 14．如图，中，DE是BC的垂直平分线，DE交AC于点E，连接BE， 若BE=9，BC=12，则cosC= ‎ 答案：；‎ ． ‎ ‎15．若两个相似三角形的周长比为2：3，则它们的面积比是 ‎ 答案：4：9；‎ ． ‎ ‎16．如图，△ABC三边的中线AD，BE，CF的公共点G，若，则图中阴影部分面积是 ‎ 答案：4；‎ ． ‎ 三、解答题（一）（本题共3题，每小题6分，共18分）‎ ‎17．计算： ． （‎ 答案：解：原式==；‎ ） ‎ ‎18．已知：边长为1的一个正方形和一个等边三角形如图摆放，求则△ABC的面积．（‎ 答案：解：过点C作CD和CE垂直正方形的两个边长，如图，‎ ‎∵一个正方形和一个等边三角形的摆放，∴四边形DBEC是矩形，‎ ‎∴CE=DB=，∴△ABC的面积=AB•CE=×1×=， ‎ ）‎ ‎19．如图，已知MN表示某引水工程的一段设计路线，从M到N的走向为南偏东30°，在M的南偏东60°方向上有一点A，以A为圆心，500m为半径的圆形区域为居民区。取MN上另一点B，测得BA的方向为南偏东75°．已知MB=400m，通过计算回答，如果不改变方向，输水线路是否会穿过居民区？（‎ 答案：解：不会穿过居民区。‎ 过A作AH⊥MN于H，则∠ABH=45°，AH=BH 设AH=x，则BH=x，MH=x=x+400，∴x=200+200=546．4＞500∴不会穿过居民区。‎ ）‎ 四、解答题（二）（本题共3题，每小题7分，共21分）‎ ‎20．小丽为了测旗杆AB的高度，小丽眼睛距地图1．5米，小丽站在C点，测出旗杆A的仰角为30o，小丽向前走了10米到达点E，此时的仰角为60o，求旗杆的高度．（‎ 答案：解：由题意，，‎ ‎∴．∴．∴．‎ ‎∴．‎ ‎∵，∴ ． 答：（略）‎ ）‎ ‎21．如图，平台AB高为12m，在B处测得楼房CD顶部点D的仰角为45°，底部点C的俯角为30°，求楼房CD的高度(＝1．7)． （‎ 答案：解：如图，过点B作BE⊥CD于点E， ‎ 根据题意，∠DBE=45°，∠CBE=30°． ∵AB⊥AC，CD⊥AC， ∴四边形ABEC为矩形． ‎ ‎∴CE=AB=12m． ‎ 在Rt△CBE中，cot∠CBE= ∴BE=CE•cot30°=12×=12． ‎ 在Rt△BDE中，由∠DBE=45°， 得DE=BE=12． ‎ ‎∴CD=CE+DE=12（+1）≈32．4． ‎ 答：楼房CD的高度约为32．4m． ‎ ‎ ‎ ） ‎ A B C D ‎30°‎ ‎45°‎ 第21题图 ‎22．如图，等边△ABC的边长是2，D、E分别为AB、AC的中点，延长BC至点F，使CF= BC，‎ 连接CD和EF．‎ ‎（1）求证：DE=CF； （2）求EF的长．（‎ 答案：（1）证明：∵D、E分别为AB、AC的中点，∴DEBC，‎ ‎∵延长BC至点F，使CF= BC，∴DEFC， 即DE=CF；‎ ‎（2）解：∵DEFC，∴四边形DEFC是平行四边形，∴DC=EF，‎ ‎∵D为AB的中点，等边△ABC的边长是2，∴AD=BD=1，CD⊥AB，BC=2，∴DC=EF=．‎ ）‎ 五、解答题（三）（本题共3题，每小题9分，共27分）‎ ‎23．如图，已知△ABC．按如下步骤作图： ①以A为圆心，AB长为半径画弧； ②以C为圆心，CB长为半径画弧，两弧相交于点D； ③连结BD，与AC交于点E，连结AD，CD． （1）求证：△ABC≌△ADC； （2）若∠BAC = 30°，∠BCA = 45°，AC = 4，求BE的长．（‎ 答案：解：（1）证明：由作法可知：，‎ 又∵，∴△ABC≌△ADC ‎（2）由（1）可得，，∴AE⊥BD，即AC⊥BE．‎ 在Rt△ABE中，∠BAC=30°，∴AE =BE．‎ 在Rt△BEC中，∠BCE=45°，∴EC = BE．‎ 又AE + EC = AC = 4，∴BE + BE = 4． ∴BE =． ∴BE的长为．‎ ） ‎ ‎24．如图，AC是⊙O的直径，点B在⊙O上，∠ACB=30°．‎ ‎（1）利用尺规作∠ABC的平分线BD，交AC于点E，交⊙O于点D，连接CD（保留作图痕迹，不写作法）；‎ ‎（2）在（1）所作的图形中，求与的面积之比．（‎ 答案：解：（1）作图如下：‎ ‎（2）如答图2，过点作于点，过点作于点，‎ 设，‎ ‎∵AC是⊙O的直径，∴．‎ ‎∵∠ACB=30°，∴．‎ ‎∵BD是∠ABC的平分线，∴．‎ ‎∴．∴．‎ 又∵，∴． ‎ ）‎ ‎25．如图，在▱ABCD中，对角线AC、BD相交于点O，点E、F是AD上的点，且AE=EF=FD．‎ 连接BE、BF，使它们分别与AO相交于点G、H． ‎ ‎（1）求EG：BG的值； ‎ ‎（2）求证：AG=OG； ‎ ‎（3）设AG=a，GH=b，HO=c，求a：b：c的值．（‎ 答案：解：（1）∵四边形ABCD是平行四边形，∴AO=AC，AD=BC，AD∥BC，‎ ‎∴△AEG∽△CBG， ∴==． ∵AE=EF=FD， ∴BC=AD=3AE，‎ ‎∴GC=3AG，GB=3EG， ∴EG：BG=1：3；‎ ‎（2）∵GC=3AG（已证），∴AC=4AG，∴AO=AC=2AG， ∴GO=AO﹣AG=AG；‎ ‎（3）∵AE=EF=FD，∴BC=AD=3AE，AF=2AE．∵AD∥BC，∴△AFH∽△CBH，‎ ‎∴===，∴=，即AH=AC．∵AC=4AG，∴a=AG=AC，‎ b=AH﹣AG=AC﹣AC=AC，c=AO﹣AH=AC﹣AC=AC，‎ ‎∴a：b：c=：：=5：3：2．‎ ） ‎