河北省中考数学试卷及答案WORD版答案详解版 10页

‎2011河北省初中毕业生升学文化课考试 数 学 试 卷 本试卷分卷Ⅰ和卷Ⅱ两部分：卷I为选择题，卷Ⅱ为非选择题.‎ 本试卷满分为120分，考试时间为120分钟.‎ 卷Ⅰ（选择题，共30分）‎ 注意事项：1．答卷Ⅰ前，考生务必将自己的姓名、准考证号、科目填涂在答题卡，考试结束，监考人员将试卷和答题卡一并收回.‎ ‎2．每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑，答在试卷上无效.‎ ‎1‎ ‎2‎ 图1‎ 一、选择题（本大题共12个小题.1－6小题，每小题2分，7－12小题，每小题3分，共30分，在每小题给出的四个选项中，只有一项是符合题目要求的 ‎1．计算30的结果是 A．3 B．30 C．1 D．0 ‎ ‎2．如图1，∠1＋∠2等于 A．60° B．90° C．110° D．180° ‎ ‎3．下列分解因式正确的是 A．－a＋a3=－a(1＋a2) B．2a－4b＋2=2(a－2b) ‎ C．a2－4=(a－2)2 D．a2－2a＋1=(a－1)2 ‎ ‎4．下列运算中，正确的是 A．2x－x=1 B．x＋x4=x5 C．(－2x)3=－6x3 D．x2y÷y=x2 ‎ ‎5．一次函数y=6x＋1的图象不经过 A．第一象限 B．第二象限 C．第三象限 D．第四象限 ‎ ‎6．将图2①围成图2②的正方体，则图②中的红心“”标志所在的正方形是正方体中的 Y ‎①‎ ‎②‎ A B C D E F H G 图2‎ A．面CDHE ‎ B．面BCEF ‎ C．面ABFG ‎ D．面ADHG ‎ ‎7．甲、乙、丙三个旅行团的游客人数都相等，且每团游客的平均年龄都是32岁，这三个团游客年龄的方并有分别是，，，导游小王最喜欢带游客年龄相近的团队，若在这三个团中选择一个，则他应选 A．甲团 B．乙团 C．丙团 D．甲或乙团 ‎8．一小球被抛出后，距离地面的高度h（米）和飞行时间t（秒）满足下面的函数关系式：h=－5(t－1)2＋6，则小球距离地面的最大高度是 A．1米 B．5米 C．6米 D．7米 ‎9．如图3，在△ABC中，∠C=90°，BC=6，D，E分别在AB，AC上，将△ABC沿DE折叠，使点A落在A′处，若A′为CE的中点，则折痕DE的长为 A． B．5米 C．6米 D．7米 ‎10．已知三角形三边长分别为2，x，13，若x为正整数，则这样的三角形个数为 x y x 图4‎ A．2 B．3 C．5 D．13‎ ‎11．如图4，在长形中截取两个相同的圆作为圆柱的上、下底面，剩余的矩形作为圆住的侧面，刚好能组合成圆住.设矩形的长和宽分别为y和x，则y与x的函数图象大致是 x y O x y O x y O x y O A．‎ B．‎ C．‎ D．‎ 输入非零数x 取倒数 ‎×2‎ 取相反数 取倒数 ‎×4‎ x＜0‎ x＞0‎ 输出y ‎①‎ y M Q P O x ‎②‎ 图5‎ ‎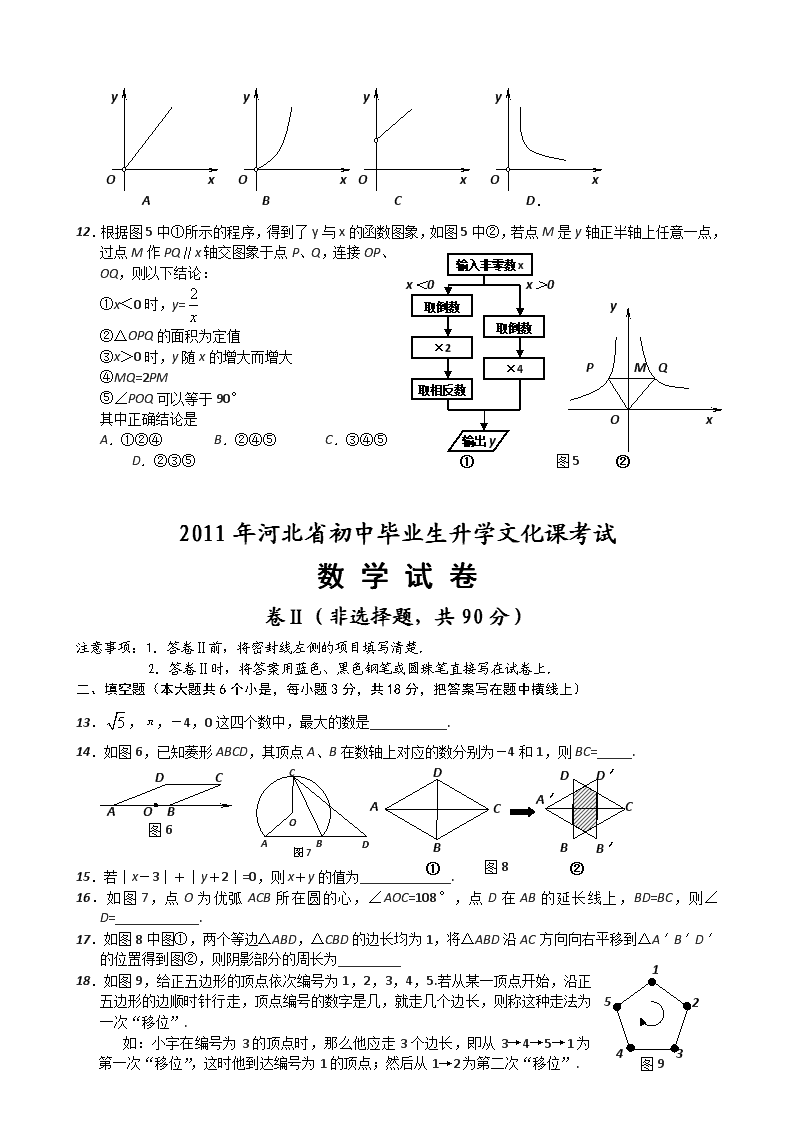12．根据图5中①所示的程序，得到了y与x的函数图象，如图5中②，若点M是y轴正半轴上任意一点，过点M作PQ∥x轴交图象于点P、Q，连接OP、OQ，则以下结论：‎ ‎①x＜0时，y=‎ ‎②△OPQ的面积为定值 ‎③x＞0时，y随x的增大而增大 ‎④MQ=2PM ‎⑤∠POQ可以等于90°‎ 其中正确结论是 A．①②④ B．②④⑤ C．③④⑤ D．②③⑤‎ ‎2011年河北省初中毕业生升学文化课考试 数 学 试 卷 卷Ⅱ（非选择题，共90分）‎ 注意事项：1．答卷Ⅱ前，将密封线左侧的项目填写清楚.‎ ‎2．答卷Ⅱ时，将答案用蓝色、黑色钢笔或圆珠笔直接写在试卷上.‎ 二、填空题（本大题共6个小是，每小题3分，共18分，把答案写在题中横线上）‎ ‎13．，π，－4，0这四个数中，最大的数是___________.‎ A B C D B D C A′‎ B′‎ D′‎ ‎①‎ ‎②‎ 图8‎ ‎14．如图6，已知菱形ABCD，其顶点A、B在数轴上对应的数分别为－4和1，则BC=_____.‎ A B C D O 图7‎ A B C D O 图6‎ ‎15．若︱x－3︱＋︱y＋2︱=0，则x＋y的值为_____________.‎ ‎16．如图7，点O为优弧ACB所在圆的心，∠AOC=108°，点D在AB的延长线上，BD=BC，则∠D=____________.‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ 图9‎ ‎17．如图8中图①，两个等边△ABD，△CBD的边长均为1，将△ABD沿AC方向向右平移到△A′B′D′的位置得到图②，则阴影部分的周长为_________‎ ‎18．如图9，给正五边形的顶点依次编号为1，2，3，4，5.若从某一顶点开始，沿正五边形的边顺时针行走，顶点编号的数字是几，就走几个边长，则称这种走法为一次“移位”.‎ 如：小宇在编号为3的顶点时，那么他应走3个边长，即从3→4→5→1为第一次“移位”，这时他到达编号为1的顶点；然后从1→2为第二次“移位”.‎ 若小宇从编号为2的顶点开始，第10次“移位”后，则他所处顶点的编号是____________.‎ 三、解答题（本大题共8个小题，共72分，解答应写出文字说明、证明过程 或演算步骤）‎ ‎19．（本小题满分8分）‎ 已知是关于x，y的二元一次方程的解.‎ 求(a＋1)(a－1)＋7的值 ‎20．（本小题满分8分）‎ 如图10，在6×8的网格图中，每个小正方形边长均为1，点O和△ABC的顶点均为小正方形的顶点.‎ ‎⑴以O为位似中心，在网格图中作△A′B′C′，使△A′B′C′和△ABC位似，且位似比为1：2‎ ‎⑵连接⑴中的AA′，求四边形AA′C′C的周长.（结果保留根号）‎ A B C O ‎21．（本小题满分8分）‎ ‎－1‎ ‎1‎ ‎2‎ 图11‎ 小宇 小静 如图11，一转盘被等分成三个扇形，上面分别标有关－1，1，2中的一个数，指针位置固定，转动转盘后任其自由停止，这时，鞭个扇形恰好停在指针所指的位置，并相应得到这个扇形上的数（若指针恰好指在等分线上，当做指向右边的扇形）.‎ ‎⑴若小静转动转盘一次，求得到负数的概率；‎ ‎⑵小宇和小静分别转动一次，若两人得到的数相同，则称两人“不谋而合”，用列表法（或画树形图）求两人“不谋而合”的概率.‎ ‎22．（本小题满分8分）‎ 甲、乙两人准备整理一批新到的实验器材，若甲单独整理需要40分钟完工，若甲、乙共同整理20分钟后，乙需再单独整理20分钟才能完工.‎ ‎⑴问乙单独整理多少分钟完工？‎ ‎⑵若乙因式作需要，他的整理时间不超过30分钟，则甲至少整理多少分钟才能完工？‎ ‎23．（本小题满分9分）‎ 如图12，四边形ABCD是正方形，点E，K分别在BC，AB上，点G在BA的延长线上，且CE=BK=AG.‎ A B C D E K G 图11‎ ‎⑴求证：①DE=DG；‎ ‎②DE⊥DG；‎ ‎⑵尺规作图：以线段DE，DG为边作出正方形DEFG（要求：只保留作图痕迹，不写作法和证明）；‎ ‎⑶连接⑵中的KF，猜想并写出四边形CEFK是怎样的特殊四边形，并证明你的猜想；‎ ‎⑷当时，衣直接写出的值.‎ ‎24．（本小题满分9分）‎ 已知A、B两地的路程为240千米，某经销商每天都要用汽车或火车将x吨保鲜品一次性由A地运往B地，受各种因素限制，下一周只能采用汽车和火车中的一种进行运输，且须提前预订.‎ 图13①‎ 火车 汽车 S(千米)‎ t(时)‎ ‎2‎ ‎120‎ ‎200‎ O 现在有货运收费项目及收费标准表，行驶路程S（千米）与行驶时间t（时）的函数图象（如图13中①），上周货运量折线统计图（如图13中②）等信息如下：‎ 货运收费项目及收费标准表 运输工具 运输费单价 元/（吨•千米）‎ 冷藏单价 元/（吨•时）‎ 固定费用 元/次 汽车 ‎2‎ ‎5‎ ‎200‎ 火车 ‎1.6‎ ‎5‎ ‎2280‎ ‎⑴汽车的速度为__________千米/时，‎ ‎17‎ ‎18‎ ‎19‎ ‎20‎ ‎21‎ ‎22‎ ‎23‎ ‎24‎ ‎25‎ ‎17‎ ‎20‎ ‎19‎ ‎22‎ ‎22‎ ‎23‎ ‎24‎ 周一 周二 周三 周四 周五 周六 周日 时间 货运量（吨）‎ 图13 ②‎ 火车的速度为_________千米/时；‎ 设每天用汽车和火车运输的总费用分别为y汽（元）和y火（元），分别求y汽、y火与x的函数关系式（不必写出x的取值范围）及x为何值时y汽＞y火；‎ ‎（总费用=运输费＋冷藏费＋固定费用）‎ ‎⑶请你从平均数、折线图走势两个角度分析，建议该经销商应提前下周预定哪种运输工具，才能使每天的运输总费用较省？‎ ‎25．（本小题满分10分）‎ 如图14①至图14④中，两平行线AB、CD音的距离均为6，点M为AB上一定点.‎ 思考：‎ B A D C ‎6‎ 图14 ①‎ B A D C ‎6‎ 图14 ③‎ B A D C ‎6‎ 图14 ②‎ B A D C ‎6‎ 图14 ④‎ α P O O O O P P P M M M M N N α α 如图14①中，圆心为O的半圆形纸片在AB、CD之间（包括AB、CD），其直径MN在AB上，MN=8，点P为半圆上一点，设∠MOP=α，‎ 当α=________度时，点P到CD的距离最小，最小值为____________.‎ 探究一 在图14①的基础上，以点M为旋转中心，在AB、CD之间顺时针旋转该半圆形纸片，直到不能再转动为止.如图14②，得到最大旋转角∠BMO=_______度，此时点N到CD的距离是______________.‎ 探究二 将图14①中的扇形纸片NOP按下面对α的要求剪掉，使扇形纸片MOP绕点M在AB、CD之间顺时针旋转.‎ ‎⑴如图14③，当α=60°时，求在旋转过程中，点P到CD的最小距离，并请指出旋转角∠BMO的最大值：‎ ‎⑵如图14④，在扇形纸片MOP旋转过程中，要保证点P能落在直线CD上，请确定α的取值范围.‎ ‎（参考数据：sin49°=，cos41°=，tan37°=）‎ ‎26．(本小题满分12分)‎ 如图15，在平面直角坐标系中，点P从原点O出发，沿x轴向右以每秒1个单位长的速度运动t（t＞0）秒，抛物线y=x2＋bx＋c经过点O和点P.已知矩形ABCD的三个顶点为A（1，0）、B（1，－5）、D（4，0）.‎ ‎⑴求c、b（用含t的代数式表示）；‎ ‎⑵当4＜t＜5时，设抛物线分别与线段AB、CD交于点M、N.‎ ‎①在点P的运动过程中，你认为∠AMP的大小是否会变化？若变化，说明理由；若不变，求出∠AMP的值；‎ ‎②求△MPN的面积S与t的函数关系式，并求t为何值时，S=；‎ ‎③在矩形ABCD的内部（不含边界），把横、纵坐标都是整数的点称为“好点”.若抛物线将这些“好点”分成数量相等的两部分，请直接写出t的取值范围.‎ A D P O ‎－1‎ M N C B x y ‎1‎ 图15‎