河南中考数学九年级知识及四边形试题专辑 16页

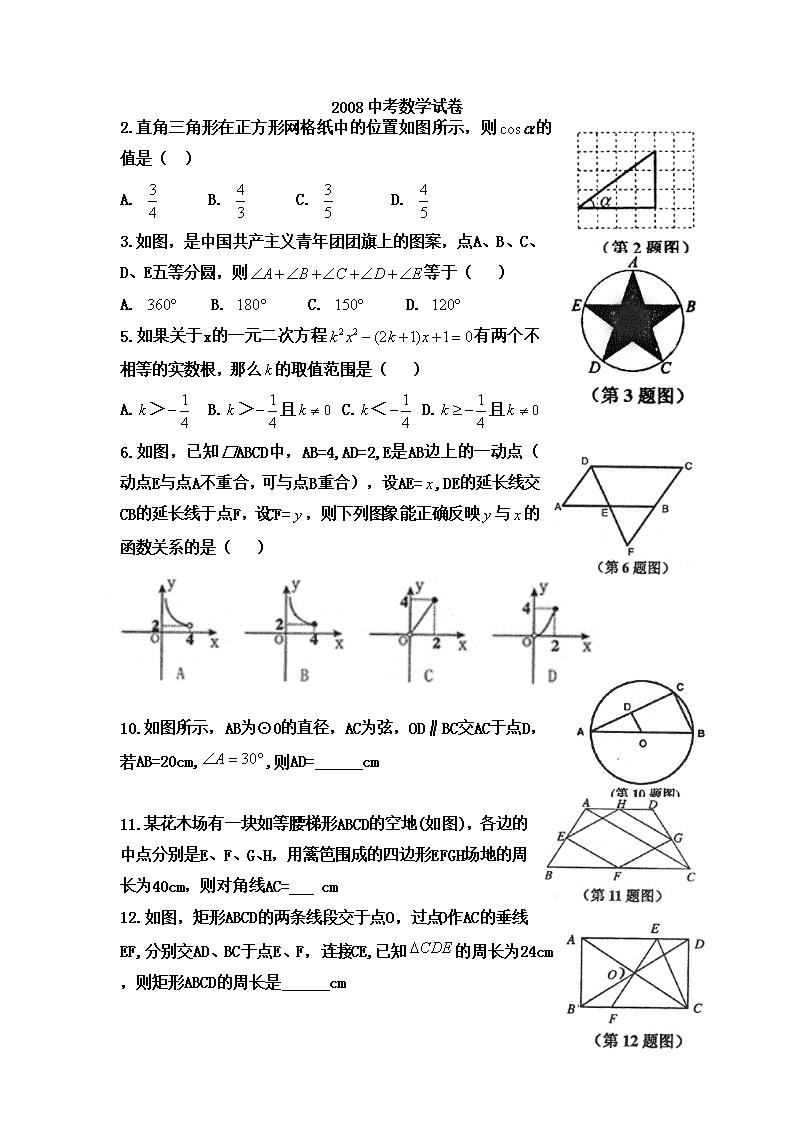
2008 中考数学试卷 2.直角三角形在正方形网格纸中的位置如图所示，则 的 值是（ ） A. B. C. D. 3.如图，是中国共产主义青年团团旗上的图案，点A、B、C、 D、E五等分圆，则 等于（ ） A. B. C. D. 5.如果关于x的一元二次方程 有两个不 相等的实数根，那么 的取值范围是（ ） A. ＞ B. ＞ 且 C. ＜ D. 且 6.如图，已知□ABCD中，AB=4,AD=2,E是AB边上的一动点（ 动点E与点A不重合，可与点B重合），设AE= ,DE的延长线交 CB的延长线于点F，设CF= ，则下列图象能正确反映 与 的 函数关系的是（ ） 10.如图所示，AB为⊙0的直径，AC为弦，OD∥BC交AC于点D， 若AB=20cm, ,则AD= cm 11.某花木场有一块如等腰梯形ABCD的空地(如图)，各边的 中点分别是E、F、G、H，用篱笆围成的四边形EFGH场地的周 长为40cm，则对角线AC= cm 12.如图，矩形ABCD的两条线段交于点O，过点O作AC的垂线 EF,分别交AD、BC于点E、F，连接CE,已知 的周长为24cm ，则矩形ABCD的周长是 cm cosα 4 3 3 4 5 3 5 4 A B C D E∠ + ∠ + ∠ + ∠ + ∠ °360 °180 °150 °120 2 2 (2 1) 1 0k x k x− + + = k k 1 4 − k 1 4 − 0k ≠ k 1 4 − 1 4k ≥ − 0k ≠ x y y x °=∠ 30A CDE∆ 13、在一幅长50cm，宽30cm的风景画的四周镶一条金色纸边，制成一幅矩形挂 图，如图所示，如果要使整个规划土地的面积是1800cm ，设金色纸边的宽为 cm，那么 满足的方程为 14、如图是二次函数 图像的一部分，该图在 轴右侧与 轴交点 的坐标 是 15、如图，直线 ( ＞0)与双曲线 在第一象限内的交点面积为R ，与 轴的交点为P，与 轴的交点为Q；作RM⊥ 轴于点M，若△OPQ与△PRM的 面积是4：1，则 17. (本小题满分 9 分) 如图,已知:在四边形 ABFC 中， =90 的垂直平分线 EF 交 BC 于点 D,交 AB 于点 E,且 CF=AE (1) 试探究,四边形 BECF 是什么特殊的四边形; (2) 当 的大小满足什么条件时,四边形 BECF 是正方形?请回答并证明你的结 论. (特别提醒:表示角最好用数字) 2 x x 2)1( 2 ++= xay y x 2−== kxy k x ky = x y x =k ACB∠ BC,° A∠ 18. (本小题满分 9 分) 已知 是关于 的一元二次方程 的两个实数根，且 — — =115 (1)求 k 的值；（2）求 + +8 的值。 21、（本题满分 10 分） 如图，在小山的西侧 A 处有一热气球，以 30 米/分钟的速度沿着与垂直方向 所成夹角为 30°的方向升空，40 分钟后到达 C 处，这时热气球上的人发现，在 A 处的正东方向有一处着火点 B，十分钟后，在 D 处测得着火点 B 的俯角为 15 °，求热气球升空点 A 与着火点 B 的距离。（结果保留根号，参考数据： ( ， ， ， ）。 22、（本题满分 10 分） 如图，△ABC 内接于⊙O，过点 B 作⊙O 的切线，交于 CA 的延长线于点 E，∠EBC=2∠C.(1)求证：AB=AC；(2)当 = 时，①求 tan∠ABE 的值；②如果 AE= ，求 AC 的 值。 23、（本题满分 11 分） 如图，抛物线 与 轴交于 A、B 两点（点 2x 2x x 062 =+− kxx 2 1x 2 2x 1x 2x 2 1x 2 2x 4 2615sin −=° 4 2615cos +=° 3215tan −=° 3215cot +=° BC AB 4 5 11 20 cbxaxy ++= 2 x A 在点 B 左侧），与 y 轴交于点 C ，且当 =O 和 =4 时，y 的值相等。直线 y=4x-16 与这条抛物线相交于两点，其中一点的横坐标是 3，另一点是这条抛物 线的顶点 M。(1)求这条抛物线的解析式； (2)P 为线段 OM 上一点，过点 P 作 PQ⊥ 轴于点 Q。若点 P 在线段 OM 上运动（点 P 不与点 O 重合，但可以与点 M 重合），设 OQ 的长为 t，四边形 PQCO 的面积为 S，求 S 与 t 之间的函数关系式及自变量 t 的取值范围； (3)随着点 P 的运动，四边形 PQCO 的面积 S 有最大值吗？如果 S 有最大值请求 出 S 的最大值并指出点 Q 的具体位置和四边形 PQCO 的特殊形状；如果 S 没有最 大值，请简要说明理由； (4)随着点 P 的运动，是否存在 t 的某个值，能满足 PO=OC？如果存在，请求出 t 的值。 2009 河南中考数学试卷 3.下列调查适合普查的是 【 】 （A）调查 2009 年 6 月份市场上某品牌饮料的质量 （B）了解中央电视台直播北京奥运会开幕式的全国收视率情况 (C) 环保部门调查 5 月份黄河某段水域的水质量情况 (D)了解全班同学本周末参加社区活动的时间 4.方程 =x 的解是 【 】 （A）x=1 （B）x=0 (C) x1=1 x2=0 (D) x1=﹣1 x2=0 10.如图,在 ABCD 中，AC 与 BD 交于点 O，点 E 是 BC 边的中 点，OE=1,则 AB 的长是 . 11.如图，AB 为半圆 O 的直径，延长 AB 到点 P，使 BP= AB，PC 切半圆 O 于点 C，点 D 是 上和点 C 不重合的一点，则 的度数为 . 13.在一个不透明的袋子中有 2 个黑球、3 个白球，它们除颜色 外其他均相同.充分摇匀后,先摸出 1 个球不放回,再摸出 1 个球,那么两个球都 是黑球的概率为 . 14.动手操作：在矩形纸片 ABCD 中，AB=3,AD=5.如图所示， 折叠纸片，使点 A 落在 BC 边上的 A’处，折痕为 PQ，当点 A’在 BC 边上移动时，折痕的端点 P、Q 也随之移动.若限定 x x x 2x  1 2 AC D∠ 点 P、Q 分别在 AB、AD 边上移动，则点 A’在 BC 边上可移 动的最大距离为 . 15.如图，在半径为 ，圆心角等于 450 的扇形 AOB 内部 作一个正方形 CDEF，使点 C 在 OA 上，点 D、E 在 OB 上， 点 F 在 上，则阴影部分的面积为（结果保留 ） . 17.（9 分）如图所示，∠BAC=∠ABD,AC=BD，点 O 是 AD、BC 的交点，点 E 是 AB 的中点.试判断 OE 和 AB 的位置关系,并给出证明. 20.(9 分)如图所示，电工李师傅借助梯子安装天花板上距地面 2 .90m 的顶灯. 已知梯子由两个相同的矩形面组成，每个矩形面的长都被六条踏板七等分，使 用时梯脚的固定跨度为 1m．矩形面与地面所成的角α为 78°.李师傅的身高为 l.78m，当他攀升到头顶距天花板 0.05～0.20m 时，安装起来比较方便.他现在 竖直站立在梯子的第三级踏板上，请你通过计算判断他安装是否比较方便? (参考数据：sin78°≈0.98，cos78°≈0.21，tan78°≈4.70.) 21. (10 分)如图，在 Rt△ABC 中，∠ACB=90°, ∠B =60°， BC=2．点 0 是 AC 的中点，过点 0 的直线 l 从与 AC 重合的位置开始，绕点 0 作逆时针旋转，交 AB 边于点 D.过点 C 作 CE∥AB 交直线 l 于点 E，设直 线 l 的旋转角为α. (1)①当α=________度时，四边形 EDBC 是等腰梯形， 此时 AD 的长为_________； 5 AB π ②当α=________ 度时，四边形 EDBC 是直角梯形，此时 AD 的长为 _________； (2)当α=90°时,判断四边形 EDBC 是否为菱形，并说明理由． 22. (10 分)某家电商场计划用 32400 元购进“家电下乡”指定产品中的电视机、 冰箱、洗衣机共 l5 台.三种家电的进价和售价如下表所示： (1) 在 不 超 出 现 有 资 金的前提下，若购进电视机的数量和冰箱的数量相同，洗衣机数量不大于电视机 数量的一半，商场有哪几种进货方案? (2)国家规定：农民购买家电后，可根据商场售价的 13％领取补贴.在(1)的 条件下． 如果这 15 台家电全部销售给农民，国家财政最多需补贴农民多少元? 23.（11 分）如图，在平面直角坐标系中，已知矩形 ABCD 的三个顶点 B（4， 0）、C（8，0）、D（8，8）.抛物线 y=ax2+bx 过 A、C 两点. (1)直接写出点 A 的坐标，并求出抛物线的解析式； (2)动点 P 从点 A 出发．沿线段 AB 向终点 B 运动，同时点 Q 从点 C 出发， 沿线段 CD 向终点 D 运动．速度均为每秒 1 个单位长度，运动时间为 t 秒.过点 P 作 PE⊥AB 交 AC 于点 E ①过点 E 作 EF⊥AD 于点 F，交抛物线于点 G.当 t 为何值时，线段 EG 最长? ②连接 EQ．在点 P、Q 运动的过程中，判断有几个时刻使得△CEQ 是等腰三 角形? 请直接写出相应的 t 值. （第 6 题） 2010 年河南中考数学试题 4．如图，△ABC 中，点 DE 分别是 ABAC 的中点，则下列结论：①BC=2DE； ②△ADE∽△ABC；③ ．其中正确的有【 】 （A）3 个 （B）2 个 （C）1 个 （D）0 个 5．方程 的根是【 】 （A） （B） （C） （D） 6．如图，将△ABC 绕点 C（0，-1）旋转 180°得到△ABC，设 点 A 的坐标为 则点 A 的坐标为【 】 （A） （B） （C） （D） AC AB AE AD = 032 =−x 3=x 3,3 21 −== xx 3=x 3,3 21 −== xx ),( ba ),( ba −− )1.( −−− ba )1,( +−− ba )2,( −−− ba ED CB A （第 4 题） O mD C B A （第 11 题） P E A B C D 11．如图，AB 切⊙O 于点 A，BO 交⊙O 于点 C，点 D 是 上异于 点 C、A 的一点，若∠ABO=32°，则∠ADC 的度数是______________． 12．现有点数为 2，3，4，5 的四张扑克牌，背面朝上洗匀，然后从中任意抽取 两张，这两张牌上的数字之和为偶数的概率为______________． 14．如图矩形 ABCD 中，AD=1，AD=，以 AD 的长为半径的⊙A 交 BC 于点 E， 则图中阴影部分的面积为______________________． 15．如图，Rt△ABC 中，∠C=90°，∠ABC=30°，AB=6．点 D 在 AB 边上， 点 E 是 BC 边上一点（不与点 B、C 重合），且 DA=DE，则 AD 的取值 范围是___________________． 19 ．（9 分）如图，在梯形ABCD 中，AD//BC，E 是 BC 的中 点，AD=5 ，BC=12 ，CD= ，∠C=45 °，点 P 是 BC 边上一动 点，设 PB 的长为 x． （1）当 x 的值为____________时，以点 P、A、D、E 为顶点的四边形为直 角梯形； （2）当 x 的值为____________时，以点 P、A、D、E 为顶点的四边形为平 行四边形；； （3）点 P 在 BC 边上运动的过程中，以 P、A、D、E 为顶点的四边形能否构 成菱形？试说明理由． 21．（9 分）如图，直线 与反比例函数 的 图象 交于 A ，B 两点．（1）求 、 的值；（2）直接写 出 时 x 的取值范围； （3）如图，等腰梯形 OBCD 中，BC//OD，OB=CD，OD 边在 x 轴上， ⌒ CmA 24 bxky += 1 x ky 2= )6,1( )3,(a 1k 2k 02 1 >−+ x kbxk （第 14 题） C DA B E （第 15 题） 过点 C 作 CE⊥OD 于点 E，CE 和反比例函数的图象交于点 P， 当梯形 OBCD 的面积为 12 时，请判断 PC 和 PE 的大小关系，并说明理由． 22．（10 分） （1）操作发现 如图，矩形 ABCD 中，E 是 AD 的中点，将△ABE 沿 BE 折叠 后得到△GBE，且点 G 在举行 ABCD 内部．小明将 BG 延长交 DC 于点 F，认为 GF=DF，你同意吗？说明理由． （2）问题解决 保持（1）中的条件不变，若 DC=2DF，求 的值； （3）类比探求 保持（1）中条件不变，若 DC=nDF，求 的值． 23．（11 分）在平面直角坐标系中，已知抛物线经过 A ，B ，C 三点．（1）求抛物线的解析式；（2）若点 M 为第三象限内抛物线上一动 点，点 M 的横坐标为 m， △AMB 的面积为 S．求 S 关于 m 的函数关系式，并求出 S 的最大值． （3）若点 P 是抛物线上的动点，点 Q 是直线 上的 动点， 判断有几个位置能够使得点 P、Q、B、O 为顶点的四边形为 平行四边形， 直接写出相应的点 Q 的坐标． AB AD AB AD )0,4(− )4,0( − )0,2( xy −= 2011 年河南省中考试卷数学 6. 如图，将一朵小花放置在平面直角坐标系中第三象限内的甲位置，先将 它绕原点 O 旋转 180°到乙位置，再将它向下平移 2 个单位长到丙位置，则小花 顶 点 A 在 丙 位 置 中 的 对 应 点 A ′ 的 坐 标 为 【 】 （A）（3，1） （B）（1，3） （C）（3，－1） （D）（1，1） 8.如图，在△ABC 中，AB=AC，CD 平分∠ACB，∠A=36°，则∠BDC 的度数为 . 10. 如图，CB 切⊙O 于点 B，CA 交⊙O 于点 D 且 AB 为⊙O 的直径，点 E 是 上异于点 A、D 的一点.若∠C=40°，则∠E 的度数为 . 11.点 、 是二次函数 的图象上两点，则 与 的大小关系为 （填“＞”、“＜”、“＝”）. 12.现有两个不透明的袋子， 其中一个装有标号分别为 1、2 的两个小球， 另—个装有标号分别为 2、3、4 的三个小球，小球除标号外其它均相同，从两 个袋子中各随机摸出 1 个小球，两球标号恰好相同的概率是 。 13.如图，在四边形 ABCD 中，∠A=90°，AD=4，连接 BD，BD⊥CD，∠ADB=∠ C.若 P 是 BC 边上一动点，则 DP 长的最小值为 。 14．如图是一个几何体的三视图，根据图示的数据可计算出该几何体的表 面积为 . 15.如图，在直角梯形 ABCD 中，AD∥BC，∠ABC=90°，∠C=60°，BC=2AD=2 ，点 E 是 BC 边的中点，△DEF 是等边三角形，DF 交 AB 于点 G，则△BFG 的 周长为 . ABD 1(2, )A y 2(3, )B y 2 2 1y x x= − + 1y 2y 1y 2y 3 17. （9 分）如图，在梯形 ABCD 中，AD∥BC， 延长 CB 到点 E，使 BE=AD，连接 DE 交 AB 于点 M.[来源:学#科#网 Z#X#X#K] （1）求证：△AMD≌△BME； （2）若 N 是 CD 的中点，且 MN=5，BE=2，求 BC 的长. 19、(9 分)如图所示，中原福塔(河南广 播电视塔)是世界第—高钢塔．小明所在的课 外活动小组在距地面 268 米高的室外观光层 的点 D 处，测得地面上点 B 的俯角α为 45 °，点 D 到 AO 的距离 DG 为 10 米；从地面 上的点 B 沿 BO 方向走 50 米到达点 C 处，测 得塔尖 A 的仰角β为 60°。请你根据以上数据计算塔高 AO，并求出计算结果与 实际塔高 388 米之间的误差．(参考数据： ≈1.732， ≈1.414.结果精确 到 0.1 米) 20. （9 分）如图，一次函数 与反 比例函数 的图象交于点 和 ， 与 y 轴交于点 C.（1） = ， = ； （2）根据函数图象可知，当 ＞ 时，x 的 取值范围是 ； （3）过点 A 作 AD⊥x 轴于点 D，点 P 是反比例函数在第一象限的图象上一 点.设直线 OP 与线段 AD 交于点 E，当 ： =3：1 时，求点P 的坐标. 3 2 1 1 2y k x= + 2 2 ky x = (4, )A m ( 8, 2)B − − 1k 2k 1y 2y ODACS四边形 ODES 22. （10 分）如图，在 Rt△ABC 中，∠B=90°， BC=5 ，∠C=30°.点 D 从点 C 出发沿 CA 方向以每秒 2 个单位长的速度向点 A 匀速运动，同时点 E 从点 A 出 发沿 AB 方向以每秒 1 个单位长的速度向点 B 匀速运 动，当其中一个点到达终点时，另一个点也随之停止运 动.设点 D、E 运动的时间是 t 秒（t＞0）.过点 D 作 DF⊥BC 于点 F，连接 DE、 EF. （1）求证：AE=DF； （2）四边形 AEFD 能够成为菱形吗？如果能，求出相应的 t 值；如果不能， 说明理由. （3）当 t 为何值时，△DEF 为直角三角形？请说明理由. 23. （11 分）如图，在平面直角坐标系中，直线 与抛物线 交于 A、B 两点，点 A 在 x 轴上，点 B 的横坐标为－8. （1）求该抛物线的解析式； （2）点 P 是直线 AB 上方的抛物线上一动点（不与点 A、B 重合），过点 P 作 x 轴的垂线，垂足为 C，交直线 AB 于点 D，作 PE⊥AB 于点 E. ①设△PDE 的周长为 l，点 P 的横坐标为 x，求 l 关于 x 的函数关系式，并求出 l 的最大值； ②连接 PA，以 PA 为边作图示一侧的正方形 APFG.随着 点 P 的运动，正方形的大小、位置也随之改变.当顶点 F 或 G 恰好落在 y 轴上时，直接写出对应的点 P 的坐标. 3 3 3 4 2y x= − 21 4y x bx c= − + + E F C D B G A 第 10 题 E O C D BA 第 8 题 2012 年河南中考试题数学 5.在平面直角坐标系中，将抛物线 先向右平移 2 个单位，再向上平移 2 个单位，得到的抛物线的解析式是（ ） A. B. C. D. 8.如图，已知 AB 是⊙O 的直径，且⊙O 于点 A， = .则下列结论中不一 定正确的是（ ） A. BA⊥DA B. OC//AE C. ∠COE=2∠ECA D. OD⊥AC 10.如图，在△ABC 中，∠C=90°,∠CAB=50°.按以下步骤作图： ①以点 A 为圆心，小于 AC 的长为半径画弧，分别交 AB、AC 于点 E、 F； ②分别以点 E、F 为圆心，大于 为半径画弧， 两弧相交于点 G；③作射线 AG 交 BC 边于点 D， 则∠ADC 的度数为_______。 11.母线长为 3，底面圆的直径为 2 的圆锥的侧面积为___________. 12.一个不透明的袋子中装有三个小球，它们除分别标有的数字 1、3、5 不 同外，其它完全相同。任意从袋子中摸出一球后放回，再任意摸出一球，则两 次摸出的球所标数字之和为 6 的概率为____________。 13.如图，点 A、B 在反比例函数 的图象上，过点 A、B 作 x 轴的垂线，垂足分别为 M、N，延长线段 AB 交 x 轴于点 C，若 OM=MN=NC,△AOC 的面积为 6，则 k 的值为________。 14.如图，在 Rt△ABC 中，∠C=90°，AC=6，BC=8.把△ABC 绕 AB 边上的点 D 顺时针旋转 90°得到△A′B′C′，A′C′交 AB 于点 E。若 AD=BE，则△A′DE 的面积是_________. 42 −= xy 2)2( 2 ++= xy 2)2( 2 −−= xy 2)2( 2 +−= xy 2)2( 2 −+= xy EC CB EF2 1 )0,0( >>= xkx ky xCO M B N y A 第 13 题 E C D B A 第 14 题 A′ B′ C′ E F CDB A ` 第 15 题 E CD B A 第 20 题 E F C D B G A 图 1 E F C D B G A 图 2 15.如图，在 Rt△ABC 中，∠ACB=90°，∠B=30°，BC=3，点 D 是 BC 边上 一动点（不与点 B、C重合），过点 D 作 DE⊥BC 交 AB 边于点 E，将∠B 沿直线 DE 翻折，点 B 落在射线 BC 上的点 F 处，当△AEF 为直角三角形时，BD 的长为 __________. 18.（9 分）如图，在菱形 ABCD 中，AB=2，∠DAB=60°，点 E 是 AD 边的中 点，点 M 是 AB 边上一动点（不与点 A 重合），延长 ME 交射线 CD 于点 N，连接 MD、AN。 （1）求证：四边形 AMDN 是平行四边形； （2）填空：①当 AM 的值为_____时，四边形 AMDN 是矩形； ②当 AM 的值为_______时，四边形 AMDN 是菱形。 20.（9 分）某宾馆为庆祝开业，在楼前悬挂了许多宣传条幅。如图所示， 一条幅从楼顶 A 处放下，在楼前点 C 处拉直固定。小明为了测量此条幅的长 度，他先测得楼顶 A 点的仰角为 45°，已知点 C 到大厦的距离 BC=7 米，∠ ABD=90°.请根据以上数据求条幅的长度（结果保留整数。参考数据： tan31°≈0.60,sin31°≈0.52，cos31°≈0.86）. 22.（10 分）类比转化、从特殊到一般等思想方法，在数学学习和研究中 经常用到，如下是一个案例，请补充完整。 原题：如图 1，在□ABCD 中，点 E 是 BC 边的中点，点 F 是线段 AE 上一点，BF 的延长线交射线 CD 于点 G。若 ，求 的值。 （1）尝试探究 在图 1 中，过点 E 作 EH//AB 交 BG 于点 H，则 AB 和 EH 的数量关系是 _____________，CG 和 EH 的数量关系是______________， 的值是 __________. （2）类比延伸 如图 2，在原题的条件下，若 ，则 的值是_____________ 3= EF AF CG CD CG CD )0( >= mmEF AF CG CD E CD M B N A 第 18 题 E F CD BA 图 3 第 23 题 x y A BC D P O （用含 m 的代数式表示），试写出解答过程。 （3）拓展迁移 如图 3，梯形 ABCD 中，DC//AB，点 E 是 BC 的延长线上一点，AE 和 BD 相交 于点 F。若 ， ，则 的值是__________（用含 a，b 的代数式表示）。 23.(11 分)如图，在平面直角坐标系中，直线 与抛物线 交于 A、B 两点，点 A 在 x 轴上，点 B 的纵坐标为 3。点 P 是直线 AB 下方的抛物线上一动点（不与点 A、B 重合），过点 P 作 x 轴的垂线交直线 AB 于点 C，作 PD⊥AB 于点 C，作 PD⊥AB 于点 D。 （1）求 a、b 及 sin∠ACP 的值； （2）设点 P 的横坐标为 m. ① 用含 m 的代数式表示线段 PD 的长，并求出线段 PD 长的最大 值； ②连接 PB，线段 PC 把△PDB 分成两个三角形，是否存在合适的 m 值，使这两个三角形的面积之比为 9:10？若存在，直接写 m 的值； 若不存在，说明理由。 aCD AB = )0,0( >>= babBE BC EF AF 12 1 += xy 32 −+= bxaxy