2008年浙江嘉兴数学试题 9页

‎2008年浙江省嘉兴市中考试题 数 学 卷Ⅰ（选择题）‎ 一、选择题（本题有10小题，每题4分，共40分．请选出各题中唯一的正确选项，不选、多选、错选，均不得分）‎ 1．计算的结果是（ ）‎ A． B． C． D．‎ ‎2．杭州湾跨海大桥全长约‎36000米，36000用科学记数法可表示为（ ）‎ A． B． C． D．‎ ‎（第3题）‎ 3．如图，中，已知，，，‎ 是中位线，则（ ）‎ A．4 B．3 ‎ C．2 D．1‎ ‎4．下列运算正确的是（ ）‎ A． B． ‎ C． D．‎ 5．下列图形分别是等边三角形、直角三角形、等腰梯形和矩形，其中有且只有一条对称轴的对称图形是（ ）‎ A． B． C． D．‎ ‎6．某反比例函数的图象经过点，则此函数图象也经过点（ ）‎ A． B． C． D．‎ 7．已知甲、乙两组数据的平均数分别是，，方差分别是，，比较这两组数据，下列说法正确的是（ ）‎ A．甲组数据较好 B．乙组数据较好 C．甲组数据的极差较大 D．乙组数据的波动较小 ‎8．已知等腰三角形的一个内角为，则这个等腰三角形的顶角为（ ）‎ A． B． C．或 D．或 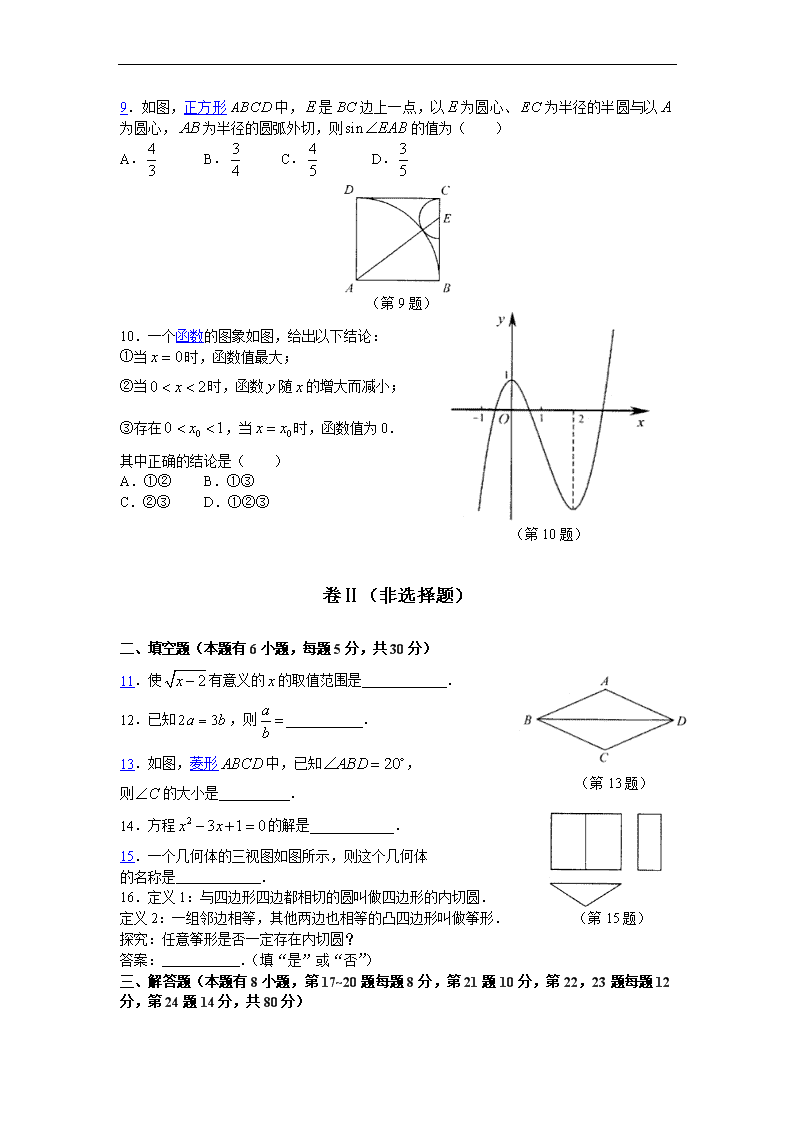9．如图，正方形中，是边上一点，以为圆心、为半径的半圆与以为圆心，为半径的圆弧外切，则的值为（ ）‎ A． B． C． D．‎ ‎（第10题）‎ ‎（第9题）‎ ‎10．一个函数的图象如图，给出以下结论：‎ ‎①当时，函数值最大；‎ ‎②当时，函数随的增大而减小；‎ ‎③存在，当时，函数值为0．‎ 其中正确的结论是（ ）‎ A．①② B．①③ ‎ C．②③ D．①②③‎ 卷Ⅱ（非选择题）‎ 二、填空题（本题有6小题，每题5分，共30分）‎ ‎（第13题）‎ 11．使有意义的的取值范围是 ．‎ ‎12．已知，则 ．‎ 13．如图，菱形中，已知，‎ 则的大小是 ．‎ ‎（第15题）‎ ‎14．方程的解是 ．‎ 15．一个几何体的三视图如图所示，则这个几何体 的名称是 ．‎ ‎16．定义1：与四边形四边都相切的圆叫做四边形的内切圆．‎ 定义2：一组邻边相等，其他两边也相等的凸四边形叫做筝形．‎ 探究：任意筝形是否一定存在内切圆？‎ 答案： ．（填“是”或“否”）‎ 三、解答题（本题有8小题，第17~20题每题8分，第21题10分，第22，23题每题12分，第24题14分，共80分）‎ 17．计算：．‎ ‎18．先化简，再求值：，其中．‎ 19．如图，A，B，C，D四张卡片上分别写有四个实数，从中任取两张卡片．‎ A B C D ‎（第19题）‎ ‎（1）请列举出所有可能的结果（用字母A，B，C，D表示）；‎ ‎（2）求取到的两个数都是无理数的概率．‎ ‎20．如图，正方形网格中，为格点三角形（顶点都是格点），将绕点按逆时针方向旋转得到．‎ ‎（第20题）‎ ‎（1）在正方形网格中，作出；‎ ‎（2）设网格小正方形的边长为1，求旋转 过程中动点所经过的路径长．‎ 21．某学校组织教师为汶川地震救灾捐款，分6个工会小组进行统计，其中第6工会小组尚未统计在内，如图：‎ ‎（第21题）‎ ‎（1）求前5个工会小组捐款金额的众数、中位数和平均数；‎ ‎（2）若全部6个小组的捐款平均数为2750元，求第6小组的捐款金额，并补全统计图．‎ ‎22．一个农机服务队有技术员工和辅助员工共15人，技术员工人数是辅助员工人数的2倍．服务队计划对员工发放奖金共计20000元，按“技术员工个人奖金”（元）和“辅助员工个人奖金”（元）两种标准发放，其中，并且都是100的整数倍．‎ 注：农机服务队是一种农业机械化服务组织，为农民提供耕种、收割等有偿服务．‎ ‎（1）求该农机服务队中技术员工和辅助员工的人数；‎ ‎（2）求本次奖金发放的具体方案．‎ ‎23．小丽参加数学兴趣小组活动，提供了下面3个有联系的问题，请你帮助解决：‎ ‎（1）如图1，正方形中，作交于，交于，求证：；‎ ‎（2）如图2，正方形中，点分别在上，点分别在上，且，求的值；‎ ‎（3）如图3，矩形中，，，点分别在上，且，求的值．‎ ‎（第23题图1）‎ ‎（第23题图2）‎ ‎（第23题图3）‎ ‎24．如图，直角坐标系中，已知两点，点在第一象限且为正三角形，的外接圆交轴的正半轴于点，过点的圆的切线交轴于点．‎ ‎（1）求两点的坐标；‎ ‎（2）求直线的函数解析式；‎ ‎（3）设分别是线段上的两个动点，且平分四边形的周长．‎ 试探究：的最大面积？‎ ‎（第24题）‎ ‎2008年浙江嘉兴市中考数学试题参考答案 一、选择题（本题有10小题，每题4分，共40分）‎ ‎1．D 2．B 3．B 4．A 5．C ‎6．A 7．D 8．C 9．D 10．C 二、填空题（本题有6小题，每题5分，共30分）‎ ‎11． 12． 13． 14．‎ ‎15．直三棱柱 16．是 三、解答题（本题有8小题，第17~20题每题8分，第21题10分，第22、23题每题12分，第24题14分，共80分）‎ ‎17．原式 ‎18．原式 当时，原式 ‎19．（1）所有可能的结果是：．‎ ‎（2）和是无理数，‎ 取到的两个数都是无理数就是取到卡片，概率是．‎ ‎（第20题）‎ ‎20．（1）如图 ‎（2）旋转过程中动点所经过的路径为一段圆弧．‎ ‎，，．‎ 又，‎ 动点所经过的路径长为．‎ ‎21．（1）众数是2500元、中位数是2500元、平均数是2700元；‎ ‎（2）设第6小组的捐款金额为元，‎ 则，解得．‎ 第6小组的捐款金额为3000元．‎ 如图：‎ ‎22．（1）设该农机服务队有技术员工人、辅助员工人，‎ 则，解得．‎ 该农机服务队有技术员工10人、辅助员工5人．‎ ‎（2）由，得．‎ ‎，，‎ 并且都是100的整数倍，‎ ‎，，．‎ 本次奖金发放的具体方案有3种：‎ 方案一：技术员工每人1600元、辅助员工每人800元；‎ 方案二：技术员工每人1500元、辅助员工每人1000元；‎ 方案三：技术员工每人1400元、辅助员工每人1200元．‎ ‎（第23题图1）‎ ‎23．（1），‎ ‎，‎ 又，，‎ ‎，‎ ‎．‎ ‎（2）作交于，‎ 作交于，‎ 则，．‎ 由（1）知，，‎ ‎（第23题图2）‎ ‎，即．‎ ‎（3）作交于，‎ 作交于，‎ 则，．‎ ‎，，‎ ‎，‎ ‎（第23题图3）‎ 又，‎ ‎，‎ ‎．‎ ‎．‎ ‎24．（1），．‎ 作于，‎ ‎（第24题）‎ 为正三角形，‎ ‎，．‎ ‎．‎ 连，，，‎ ‎．‎ ‎（第24题）‎ ‎．‎ ‎（2），是圆的直径，‎ 又是圆的切线，．‎ ‎，．‎ ‎．‎ 设直线的函数解析式为，‎ 则，解得．‎ 直线的函数解析式为．‎ ‎（3），，，，‎ 四边形的周长．‎ 设，的面积为，‎ 则，．‎ ‎．‎ 当时，．‎ 点分别在线段上，‎ ‎，解得．‎ 满足，‎ 的最大面积为．‎ ‎ ‎