资阳市2013年中考数学卷 8页

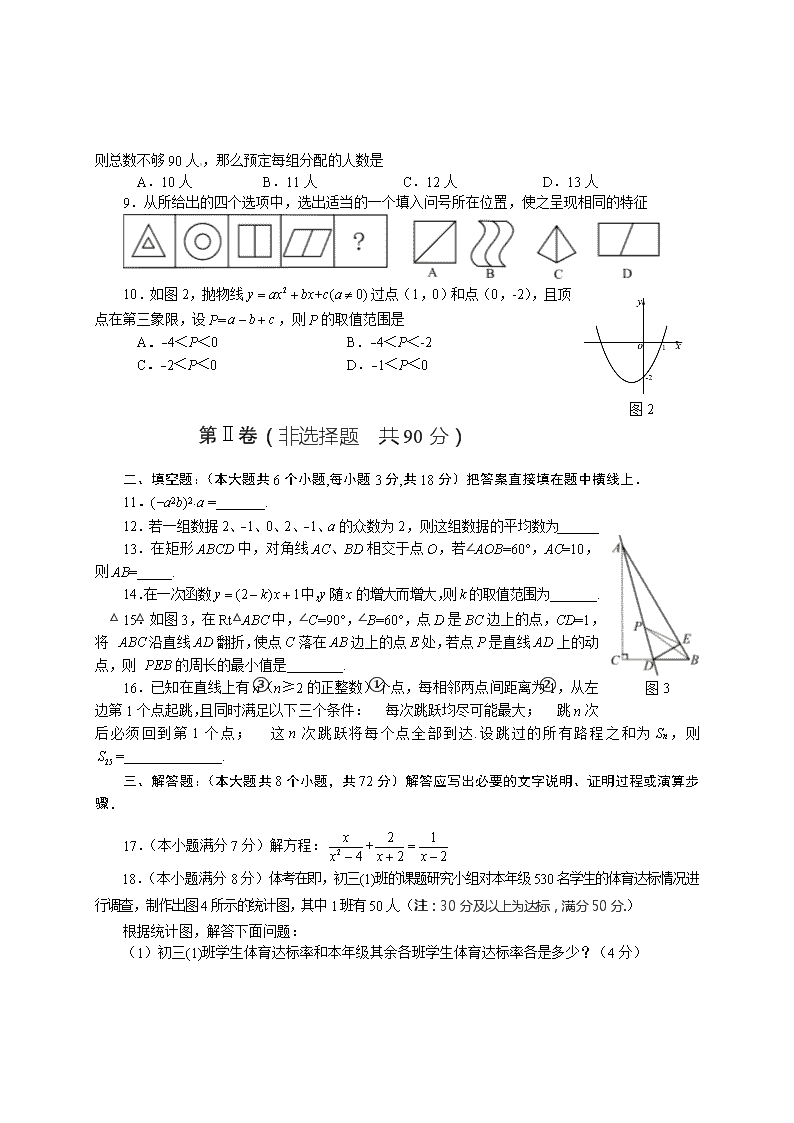
资阳市2013年高中阶段教育学校招生统一考试 数 学 全卷分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共4页。全卷满分120分。考试时间共120分钟。‎ 注意事项：‎ ‎1．答题前，请考生务必在答题卡上正确填写自己的姓名、准考证号和座位号。考试结束，将试卷和答题卡一并交回。‎ ‎2．选择题每小题选出的答案须用2B铅笔在答题卡上把对应题目的答案标号涂黑。如需改动，用橡皮擦擦净后，再选涂其它答案。非选择题须用黑色墨水的钢笔或签字笔在答题卡上对应题号位置作答，在试卷上作答，答案无效。‎ 第Ⅰ卷（选择题 共30分）‎ 一、选择题：（本大题共10个小题，每小题3分，共30分）在每小题给出的四个选项中，只有一个选项符合题意．‎ ‎1．16的平方根是 A．4 B．±‎4 ‎ C．8 D．±8‎ ‎2．一个正多边形的每个外角都等于36°，那么它是 A．正六边形 B．正八边形 C．正十边形 D．正十二边形 ‎3．在一个不透明的盒子里，装有4个黑球和若干个白球，它们除颜色外没有任何其他区别，摇匀后从中随机摸出一个球记下颜色，再把它放回盒子中，不断重复，共摸球40次，其中10次摸到黑球，则估计盒子中大约有白球 图1‎ A．12个 B．16个 C. 20个 D．30个 ‎4．在函数y =中，自变量x的取值范围是 A．x≤1 B．x≥‎1 ‎ C．x＜1 D．x＞1‎ ‎5．如图1，点E在正方形ABCD内，满足，AE=6，BE=8，则阴影部分的面积是 A． B． C． D．80‎ ‎6．资阳市2012年财政收入取得重大突破，地方公共财政收入用四舍五入法取近似值后为27.39亿元，那么这个数值 A．精确到亿位 B．精确到百分位 C．精确到千万位 D．精确到百万位 ‎7．钟面上的分针的长为1，从9点到9点30分，分针在钟面上扫过的面积是 A． B． C. D．‎ ‎8．在芦山地震抢险时，太平镇部分村庄需8组战士步行运送物资，要求每组分配的人数相同.若按每 组人数比预定人数多分配1人，则总数会超过100人；若按每组人数比预定人数少分配1人，则总数不够90人，那么预定每组分配的人数是 A．10人 B．11人 C．12人 D．13人 ‎9．从所给出的四个选项中，选出适当的一个填入问号所在位置，使之呈现相同的特征 图2‎ ‎10．如图2，抛物线过点（1，0）和点（0，-2），且顶点在第三象限，设P=，则P的取值范围是 A．-4＜P＜0 B．-4＜P＜-2‎ C．-2＜P＜0 D．-1＜P＜0 ‎ 第Ⅱ卷（非选择题 共90分）‎ 二、填空题：（本大题共6个小题,每小题3分,共18分）把答案直接填在题中横线上．‎ ‎11．(－a2b)2·a =_______.[来源:学科网ZXXK]‎ 图3‎ ‎12．若一组数据2、-1、0、2、-1、a的众数为2，则这组数据的平均数为______ ‎ ‎13．在矩形ABCD中，对角线AC、BD相交于点O，若∠AOB=60°，AC=10，则AB=_____.‎ ‎14．在一次函数中，y随x的增大而增大，则k的取值范围为_______.‎ ‎15．如图3，在Rt△ABC中，∠C=90°，∠B=60°，点D是BC边上的点，CD=1，将△ABC沿直线AD翻折，使点C落在AB边上的点E处，若点P是直线AD上的动点，则△PEB的周长的最小值是________.‎ ‎16．已知在直线上有n（n≥2的正整数）个点，每相邻两点间距离为1，从左边第1个点起跳，且同时满足以下三个条件：①每次跳跃均尽可能最大；②跳n次后必须回到第1个点；③这n次跳跃将每个点全部到达.设跳过的所有路程之和为Sn，则=______________.‎ 三、解答题：（本大题共8个小题，共72分）解答应写出必要的文字说明、证明过程或演算步骤．‎ ‎17．（本小题满分7分）解方程：‎ ‎18．（本小题满分8分）体考在即，初三(1)班的课题研究小组对本年级530名学生的体育达标情况进行调查，制作出图4所示的统计图，其中1班有50人.（注：30分及以上为达标，满分50分.）‎ 根据统计图，解答下面问题：‎ ‎（1）初三(1)班学生体育达标率和本年级其余各班学生体育达标率各是多少？（4分）‎ 图4‎ ‎（2）若除初三(1)班外其余班级学生体育考试成绩在30—40分的有120人，请补全扇形统计图；（注：请在图中注明分数段所对应的圆心角的度数）（2分）‎ ‎（3）如果要求全年级学生的体育达标率不低于90%，试问在本次调查中，该年级全体学生的体育达标率是否符合要求？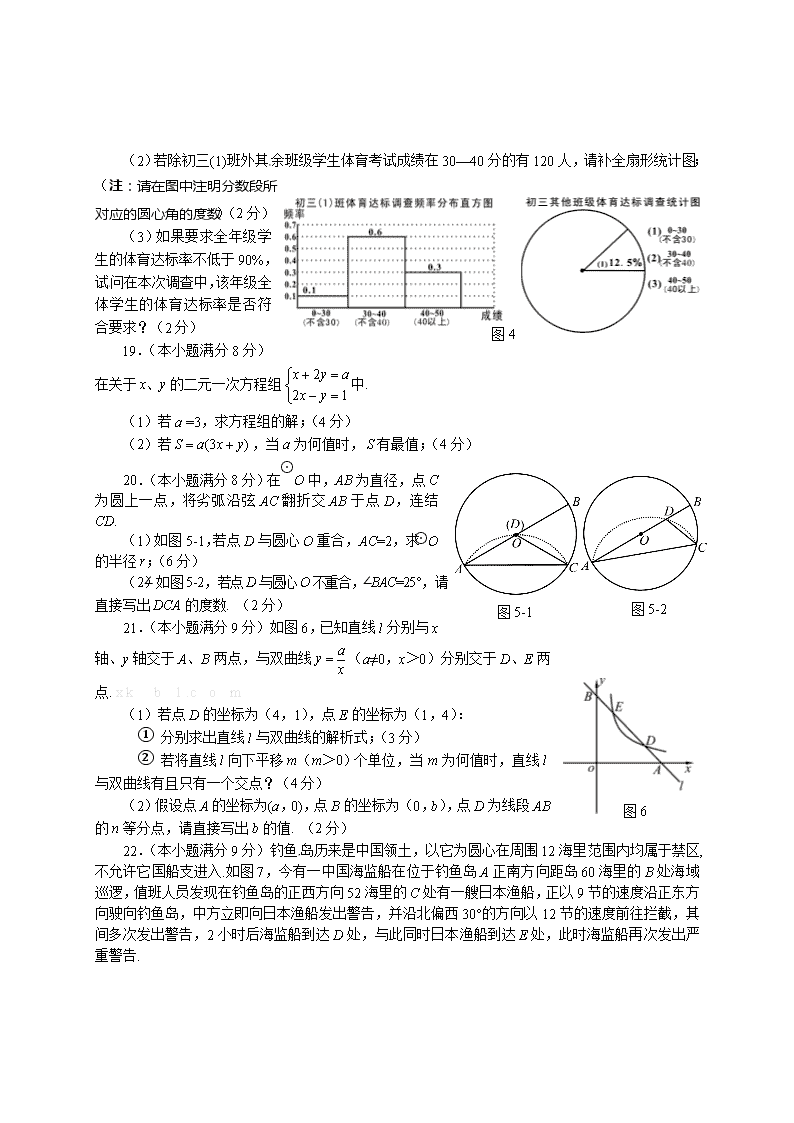（2分）‎ ‎19．（本小题满分8分）在关于x、y的二元一次方程组中.‎ ‎（1）若a =3，求方程组的解；（4分）‎ ‎（2）若，当a为何值时，有最值；（4分）‎ 图6‎ 图5-1‎ 图5-2‎ ‎20．（本小题满分8分）在⊙O中，AB为直径，点C为圆上一点，将劣弧沿弦AC翻折交AB于点D，连结CD.‎ ‎（1）如图5-1，若点D与圆心O重合，AC=2，求⊙O的半径r；（6分）‎ ‎（2）如图5-2，若点D与圆心O不重合，∠BAC=25°，请直接写出∠DCA的度数. （2分）‎ ‎21．（本小题满分9分）如图6，已知直线l分别与x轴、y轴交于A、B两点，与双曲线（a≠0，x＞0）分别交于D、E两点. x k b 1 .c o m ‎（1）若点D的坐标为（4，1），点E的坐标为（1，4）：‎ ‎① 分别求出直线l与双曲线的解析式；（3分）‎ ‎② 若将直线l向下平移m（m＞0）个单位，当m为何值时，直线l与双曲线有且只有一个交点？（4分）‎ ‎（2）假设点A的坐标为(a，0)，点B的坐标为（0，b），点D为线段AB的n等分点，请直接写出b的值. （2分）‎ ‎22．（本小题满分9分）钓鱼岛历来是中国领土，以它为圆心在周围12海里范围内均属于禁区,不允许它国船支进入.如图7，今有一中国海监船在位于钓鱼岛A正南方向距岛60海里的B处海域巡逻，值班人员发现在钓鱼岛的正西方向52海里的C处有一艘日本渔船，正以9节的速度沿正东方向驶向钓鱼岛，中方立即向日本渔船发出警告，并沿北偏西30°的方向以12节的速度前往拦截，其间多次发出警告，2小时后海监船到达D处，与此同时日本渔船到达E处，此时海监船再次发出严重警告.‎ 图7‎ ‎（1）当日本渔船收到严重警告信号后，必须沿北偏东转向多少度航行，才能恰好避免进入钓鱼岛12海里禁区？（4分）‎ ‎（2）当日本渔船不听严重警告信号，仍按原速度、原方向继续前进，那么海监船必须尽快到达距岛12海里，且位于线段AC上的F处强制拦截渔船，问海监船能否比日本渔船先到达F处？（5分）‎ ‎（注：① 中国海监船的最大航速为18节，1节=1海里/时；②参考数据：sin26.3°≈0.44，sin20.5°≈0.35，sin18.1°≈0.31，，）‎ ‎23．（本小题满分11分）在一个边长为a（单位：cm）的正方形ABCD中，点E、M分别是线段AC、CD上的动点，连结DE并延长交正方形的边于点F，过点M作MN⊥DF于H，交AD于N.‎ ‎（1）如图8-1，当点M与点C重合，求证：DF=MN；（4分）‎ ‎（2）如图8-2，假设点M从点C出发，以1cm/s的速度沿CD向点D运动，点E同时从点A出发，以cm/s速度沿AC向点C运动，运动时间为t（t＞0）：‎ ‎① 判断命题“当点F是边AB中点时，则点M是边CD的三等分点”的真假，并说明理由. （4分）‎ 图9‎ 图8-1‎ 图8-2‎ ‎② 连结FM、FN，△MNF能否为等腰三角形？若能，请写出a、t之间的关系；若不能，请说明理由. （3分）‎ ‎24.（本小题满分12分）如图9，四边形ABCD是平行四边形，过点A、C、D作抛物线，与x轴的另一交点为E，连结CE，点A、B、D的坐标分别为（-2，0）、（3，0）、（0，4）.‎ ‎（1）求抛物线的解析式；（3分）‎ ‎（2）已知抛物线的对称轴l交x轴于点F，交线段CD于点K，点M、N分别是直线l和x轴上的动点，连结MN，当线段MN恰好被BC垂直平分时，求点N的坐标；（4分）‎ ‎（3）在满足（2）的条件下，过点M作一条直线，使之将四边形AECD的面积分为3∶4的两部分，求出该直线的解析式. （5分）‎ 资阳市2013年高中阶段教育学校招生统一考试 数学试题参考答案及评分意见 说 明：‎ ‎1. 解答题中各步骤所标记分数为考生解答到这一步应得的累计分数．‎ ‎2. 参考答案一般只给出该题的一种解法，如果考生的解法和参考答案所给解法不同，请参照本答案及评分意见给分．‎ ‎3. 考生的解答可以根据具体问题合理省略非关键步骤．‎ ‎4. 评卷时要坚持每题评阅到底，当考生的解答在某一步出现错误、影响了后继部分时，如果该步以后的解答未改变问题的内容和难度，可视影响程度决定后面部分的给分，但不得超过后继部分应给分数的一半；如果这一步后面的解答有较严重的错误，就不给分；若是几个相对独立的得分点，其中一处错误不影响其他得分点的得分．‎ ‎5. 给分和扣分都以1分为基本单位．‎ ‎6. 正式阅卷前应进行试评，在试评中须认真研究参考答案和评分意见，不能随意拔高或降低给分标准，统一标准后须对全部试评的试卷予以复查，以免阅卷前后期评分标准宽严不同．‎ 一、选择题（每小题3分，共10个小题，满分30分）：‎ ‎1－5. BCADC；6－10. DACBA．‎ 二、填空题（每小题3分，共6个小题，满分18分）：‎ ‎11. ；12. ；13. 5；14. k＜2；15. ；16. 312．‎ 三、解答题（共8个小题，满分72分）：‎ ‎17. 3分 ‎ 4分 ‎ 6分 经检验，是原方程的解. 7分 ‎18. (1) 初三(1)班体育达标率为90%，‎ 初三年级其余班级体育达标率为1-12.5%=87.5%； 4分 ‎(2) 成绩在30—40分所对应的圆心角为90°，40—50分所对应的圆心角为225°. 6分 ‎(3) 全年级同学的体育达标率为（420+45）÷530≈87.8%＜90%，所以不达标. 8分 ‎19.（1）， 4分 ‎（2） 易求， 5分 则， 6分 ‎∴， 7分 ‎∴当时，有最小值. 8分 ‎20. （1） 过点O作AC的垂线交AC于E、交劣弧于F，由题意可知，OE=EF， 1分 ‎∵ OE⊥AC，∴AE=， 3分 在Rt△AOE中，， 4分 ‎∴，∴r=. 6分 ‎（2）∠DCA=40°. 8分 ‎21. (1) ①易求反比例函数的解析式为， 1分 直线AB的解析式为y = -x+5； 3分 ‎② 依题意可设向下平移m（m＞0）个单位后解析式为， 4分 由，得， 5分 ‎∵ 平移后直线l与反比例函数有且只有一个交点，∴△=，‎ ‎∴ ，（舍去）. 6分 即当时，直线l与反比例函数有且只有一个交点； 7分 ‎(2) . 9分 ‎22. (1) 过点E作⊙A的切线EG，连结AG，‎ AE=AC-CE=52-18=34，AG=12， 2分 sin∠GEA=≈0.35， 3分 ‎∴转向的角度至少应为北偏东69.5度； 4分 ‎(2) 过点D作DH⊥AB于H，‎ 由题意知，BD=24，∴DH=12，BH=12， 5分 易求四边形FDHA为矩形，∴FD=AH=60-12， 7分 ‎∴ 海监船到达F处的时间为（60-12）÷18≈ 2.2时， 8分 日本渔船到达F处的时间为（34-12）÷9≈2.4时，‎ ‎∴海监船比日本船先到达F处. 9分 ‎23. （1） 易证△ADF≌△MDN，则DF=MN； 4分 ‎（2）① 解法一：‎ 该命题为真命题. 5分 过点E作EG⊥AD于点G，‎ 依题意得，AE=，易求AG=EG=t， 6分 CM=t，DG=DM=‎ 易证△DGE≌△MDN，∴ 7分 由△ADF∽△DMN，得，‎ 又∵点F是线段AB中点，AB=AD，‎ ‎∴，∴DM=2DN，即点M是CD的三等分点. 8分 解法二：该命题为真命题. 5分 易证△AEF∽△CED，，‎ 易证△ADF∽△DMN，，‎ 又∵AD=CD，∴， 6分 依题意得：AE=，CM= t，EC=，DM=‎ ‎∴， 7分 又∵点F是线段AB中点，AB=AD，‎ ‎∴，∴DM=2DN，即点M是CD的三等分点. 8分 ‎② 假设FN=MN，由DM=AN知△AFN≌△DNM，∴AF=DN= t，‎ 又由△DAF∽△MDN，得，∴，∴，‎ ‎∴= t， t=0；‎ ‎∴FN=MN不成立； 9分 假设FN=MF，由MN⊥DF知，HN=HM，∴DN=DM=MC，此时点F与点B重合，‎ ‎∴ 当t =时, FN=MF； 10分 假设FN=MN，显然点F在BC边上，易得△MFC≌△NMD，∴FC=DM=，‎ 又由△NDM∽△DCF，∴，∴，∴‎ ‎∴=，∴，此时点F与点C重合，W wW. x kB 1.c ‎Om 即当时，FN=MN. 11分 ‎24. （1） ∵点A、B、D的坐标分别为（-2，0）、（3，0）、（0，4），‎ 且四边形ABCD是平行四边形，‎ ‎∴ AB=CD=5，则点C的坐标为（5，4）， 1分 易求抛物线的解析式为； 3分 ‎（2） 解法一：‎ 连结BD交对称轴于G，在Rt△OBD中，易求BD=5，‎ ‎∴CD=BD，则∠DCB=∠DBC，又∵∠DCB=∠CBE，∴∠DBC=∠CBE， 4分 过G作GN⊥BC于H，交x轴于N，易证GH=HN， 5分 ‎∴点G与点M重合，求出直线BD的解析式y=,‎ 根据抛物线可知对称轴方程为,则点M的坐标为（，），‎ 即GF=，BF=，∴BM=， 6分 又∵MN被BC垂直平分，∴BM=BN=，‎ ‎∴点N的坐标为（，0）； 7分 解法二：设点M（，b），点N（a，0），‎ 则MN的中点坐标为（）， 4分 求得直线BC的解析式为，代入得…① 5分 延长CB交对称轴于点Q，可求点Q的坐标为（，-1），又易得∠MQB=∠MNF，‎ ‎∴，∴…② 6分 由①、②得，，，∴点N的坐标为（，0）. 7分 ‎（3）解法一：过点M作直线交x轴于点，易求四边形AECD的面积为28，四边形ABCD的面积为20，由“四边形AECD的面积分为3:4”可知直线必与线段CD相交，设交点为， 8分 四边形的面积为，四边形的面积为，点P1的坐标为（a，0），假设点P在对称轴的左侧，则，，‎ 由△∽△，得，易求=，‎ ‎∴，‎ ‎∴=，则a= 10分 根据，M（）求出直线的解析式为， 11分 若点P在对称轴的右侧，则直线的解析式为. 12分 解法二：过点M作直线交x轴于，易求四边形AECD的面积为28，四边形ABCD的面积为20，由“四边形AECD的面积分为3∶4”可知直线必交在线段CD上， 8分 若P在对称轴的左侧，‎ 由△∽△得，S△MKQ1∶S△MFP1=25:1， 9分 又∵S△MKQ1+12-S△MFP1=14，∴S△MFP1=，则,Xk b1. C om ‎∴，根据M（），求出直线的解析式为， 11分 若点P在对称轴的右侧，则直线的解析式为. 12分 www.x kb 1.c om ‎