中考数学选择填空压轴题以及圆的大题 6页

中考数学选择、填空压轴题 一、动点问题 ‎1．如图，C为⊙O直径AB上一动点，过点C的直线交⊙O于D、E两点， 且∠ACD=45°，DF⊥AB于点F，EG⊥AB于点G，当点C在AB上运动时，设AF=，DE=，下列中图象中，能表示与的函数关系式的图象大致是（ ）‎ ‎（第3题）‎ ‎2．在中，为的中点，动点从点出发，以每秒1的速度沿的方向运动．设运动时间为，那么当 秒时，过、两点的直线将的周长分成两个部分，使其中一部分是另一部分的2倍．‎ ‎3．如图，正方形ABCD的边长为2，将长为2的线段QR的两端放在正方形的相邻的两边上同时滑动．如果Q点从A点出发，沿图中所示方向按A→B→C→D→A滑动到A止，同时点R从B点出发，沿图中所示方向按B→C→D→A→B滑动到B止，在这个过程中，线段QR的中点M所经过的路线围成的图形的面积为：A．2 B． C． D． （ ）‎ ‎4．如图，在梯形中，，点是线段上一定点，且=8．动点从点出发沿的路线运动，运动到点停止．在点的运动过程中，使为等腰三角形的点有 个 ‎5．如图在边长为2的正方形ABCD中，E，F，O分别是AB，CD，AD的中点，以O为圆心，以OE为半径画弧EF，P是弧EF上的一个动点，连结OP，并延长OP交线段BC于点K，过点P作⊙O的切线，分别交射线AB于点M，交直线BC于点G。若，则BK﹦ .‎ ‎ ‎ ‎（第4题）‎ ‎（第7题）‎ ‎（第6题）‎ ‎（第5题）‎ 二、面积与长度问题 ‎6．已知, A、B、C、D、E是反比例函数（x>0）图象上五个整数点（横、纵坐标均为整数），分别以这些点向横轴或纵轴作垂线段，由垂线段所在的正方形边长为半径作四分之一圆周的两条弧，组成如图所示的五个橄榄形（阴影部分），则这五个橄榄形的面积总和是 （用含π的代数式表示）‎ ‎7．如图，把一个棱长为3的正方体的每个面等分成9个小正方形，然后沿每个面正中心的一个正方形向里挖空（相当于挖去了7个小正方体），所得到的几何体的表面积是 （ ）‎ A．78 B．72 C．54 D．48 ‎ ‎8．如图，中，，，，分别为边 的中点，将绕点顺时针旋转到的位置，则整个旋转过程中线段所扫过部分的面积（即阴影部分面积）为：A． B． C． D． （ ）‎ ‎ ‎ ‎（第12题）‎ ‎（第11题）‎ ‎（第10题）‎ ‎（第9题）‎ ‎（第8题）‎ ‎9．在Rt△ABC内有边长分别为的三个正方形，则满足关系式 ．‎ ‎10．一张等腰三角形纸片，底边长l5cm，底边上的高长22．5cm．现沿底边依次从下往上裁剪宽度均为3cm的矩形纸条，如图所示．已知剪得的纸条中有一张是正方形，则这张正方形纸条是 ( ) ‎ ‎ A．第4张 B．第5张 C.第6张 D．第7张 ‎11．如图，直径分别为CD、CE的两个半圆相切于点C，大半圆M的弦AB与小半圆N相切于点F，且AB∥CD，AB=4，设弧CD、弧CE的长分别为x、y，线段ED的长为z，则z（x+y）= .‎ 三、多结论问题 ‎12．如图，在Rt△ABC 中，，D、E是斜边BC上两点，且∠DAE=45°，将△绕点顺时针旋转90后，得到△，连接，下列结论：①△≌△；②△∽△；③；④。其中一定正确的是 （ ） ‎ A．②④　　　　 B．①③ C．②③　　　　　 D．①④　　‎ ‎13．如图，在正方形纸片ABCD中，对角线AC、BD交于点O，折叠正方形纸片ABCD，使AD落在BD上，点A恰好与BD上的点F重合，展开后折痕DE分别交AB、AC于点E、G，连接GF.下列结论 ①∠ADG=22.5°；②tan∠AED=2；③；④四边形AEFG是菱形；⑤BE=2OG。.其中正确的结论有：A.①④⑤ B.①②④ C.③④⑤ D.②③④ ( )‎ ‎（第16题）‎ ‎（第14题）‎ ‎（第15题）‎ ‎（第13题）‎ ‎14．在矩形中，，，平分，过点作于，延长、交于点，下列结论中：①；②；③；④，其中正确的是( )‎ A．②③ B．③④ C．①②④ D．②③④ ‎ 四、函数问题 ‎15．小明从图所示的二次函数的图象中，观察得出了下面五条信息：①；②；③；④；⑤，你认为其中正确信息的个数有 （ ）‎ A．2个 B．3个 C．4个 D．5个 ‎16. 若，且二次函数的图象如图所示，则有 ：A．M>0 B. M<0 C. M=0 D. 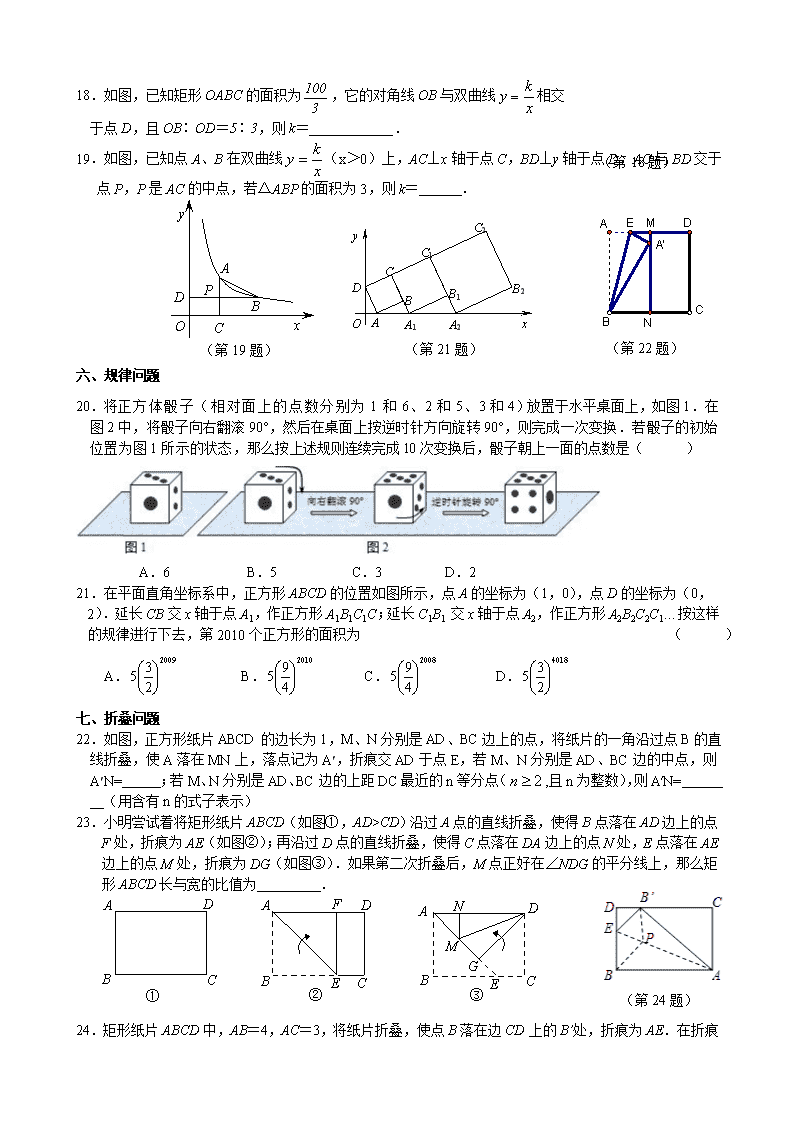M的符号不能确定 （ ）‎ ‎17．如果一条直线l经过不同的三点A(a，b)，B(b，a)，C(a-b，b-a)，那么直线l必定会经过 （ ）‎ ‎ A．第二、四象限 B.第一、二、三象限 C.第一、三象限 D.第二、三、四象限 五、反比例K值问题 ‎18．如图，已知矩形OABC的面积为，它的对角线OB与双曲线相交 ‎（第18题）‎ 于点D，且OB∶OD＝5∶3，则k＝____________．‎ ‎19．如图，已知点A、B在双曲线（x＞0）上，AC⊥x轴于点C，BD⊥y轴于点D，AC与BD交于点P，P是AC的中点，若△ABP的面积为3，则k＝ ． ‎ O A B C D A1‎ B1‎ C1‎ A2‎ C2‎ B2‎ x y y x O A B P C D ‎（第19题）‎ ‎（第22题）‎ ‎（第21题）‎ 六、规律问题 ‎20．将正方体骰子（相对面上的点数分别为1和6、2和5、3和4）放置于水平桌面上，如图1．在图2中，将骰子向右翻滚90°，然后在桌面上按逆时针方向旋转90°，则完成一次变换．若骰子的初始位置为图1所示的状态，那么按上述规则连续完成10次变换后，骰子朝上一面的点数是（ ）‎ A．6 B．5 C．3 D．2‎ ‎21．在平面直角坐标系中，正方形ABCD的位置如图所示，点A的坐标为（1，0），点D的坐标为（0，2）．延长CB交x轴于点A1，作正方形A1B1C1C；延长C1B1 交x轴于点A2，作正方形A2B2C2C1…按这样的规律进行下去，第2010个正方形的面积为 （ ）‎ A． B． C． D．‎ 七、折叠问题 ‎22．如图，正方形纸片ABCD的边长为1，M、N分别是AD、BC边上的点，将纸片的一角沿过点B的直线折叠，使A落在MN上，落点记为A′，折痕交AD于点E，若M、N分别是AD、BC边的中点，则A′N= ；若M、N分别是AD、BC边的上距DC最近的n等分点（,且n为整数），则A′N= （用含有n的式子表示）‎ A B C D A B C D E F ‎①‎ ‎②‎ A B C D E G M N ‎③‎ ‎23．小明尝试着将矩形纸片ABCD（如图①，AD>CD）沿过A点的直线折叠，使得B点落在AD边上的点F处，折痕为AE（如图②）；再沿过D点的直线折叠，使得C点落在DA边上的点N处，E点落在AE边上的点M处，折痕为DG（如图③）．如果第二次折叠后，M点正好在∠NDG的平分线上，那么矩形ABCD长与宽的比值为 ．‎ ‎（第24题）‎ ‎24．矩形纸片ABCD中，AB＝4，AC＝3，将纸片折叠，使点B落在边CD上的B’处，折痕为AE．在折痕 AE上存在一点P到边CD的距离与到点B的距离相等，则此相等距离为________．‎ ‎ 中考圆的相关压轴题 ‎【题1】如图，在Rt△ABC中，∠ACB=90°，AC=4cm，BC=3cm，⊙O为△ABC的内切圆．‎ ‎（1）求⊙ O的半径；‎ ‎（2）点P从点B沿边BA向点A以1cm/s的速度匀速运动，以P为圆心，PB长为半径作圆，设点P运动的时间为t s，若⊙P与⊙O相切，求t的值．‎ ‎【题2】阅读材料：已知，如图（1），在面积为S的△ABC中，BC=a，AC=b，AB=c，内切圆O的半径为r．连接OA、OB、OC，△ABC被划分为三个小三角形．‎ ‎∵S=S△OBC+S△OAC+S△OAB=BC•r+AC•r+AB•r=（a+b+c）r．‎ ‎∴r=．‎ ‎（1）类比推理：若面积为S的四边形ABCD存在内切圆（与各边都相切的圆），如图（2），各边长分别为AB=a，BC=b，CD=c，AD=d，求四边形的内切圆半径r；‎ ‎（2）理解应用：如图（3），在等腰梯形ABCD中，AB∥DC，AB=21，CD=11，AD=13，⊙O1与⊙O2分别为△ABD与△BCD的内切圆，设它们的半径分别为r1和r2，求的值．‎ ‎【题3】已知在平面直角坐标系xOy中，O是坐标原点，以P（1，1）为圆心的⊙P与x轴，y轴分别相切于点M和点N，点F从点M出发，沿x轴正方向以每秒1个单位长度的速度运动，连接PF，过点PE⊥PF交y轴于点E，设点F运动的时间是t秒（t＞0）‎ ‎（1）若点E在y轴的负半轴上（如图所示），求证：PE=PF；‎ ‎（2）在点F运动过程中，设OE=a，OF=b，试用含a的代数式表示b；‎ ‎（3）作点F关于点M的对称点F′，经过M、E和F′三点的抛物线的对称轴交x轴于点Q，连接QE．在点F运动过程中，是否存在某一时刻，使得以点Q、O、E为顶点的三角形与以点P、M、F为顶点的三角形相似？若存在，请直接写出t的值；若不存在，请说明理由．‎ ‎【题4】如图，矩形ABCD的边AB=3cm，AD=4cm，点E从点A出发，沿射线AD移动，以CE为直径作圆O，点F为圆O与射线BD的公共点，连接EF、CF，过点E作EG⊥EF，EG与圆O相交于点G，连接CG．‎ ‎（1）试说明四边形EFCG是矩形；‎ ‎（2）当圆O与射线BD相切时，点E停止移动，在点E移动的过程中，‎ ‎①矩形EFCG的面积是否存在最大值或最小值？若存在，求出这个最大值或最小值；若不存在，说明理由；‎ ‎②求点G移动路线的长．‎ ‎【题6】如图，在△ABC中，∠B=45°，∠ACB=60°，，点D为BA延长线上的一点，且∠D=∠ACB，⊙O为△ABC的外接圆.‎ ‎（1）求BC的长；‎ ‎（2）求⊙O的半径.‎ ‎【题7】为了考察冰川融化的状况，一支科考队在某冰川上设一定一个以大本营O为圆心，半径为4km 圆形考察区域，线段P1、P2‎ 是冰川的部分边界线（不考虑其它边界），当冰川融化时，边界线沿着与其垂直的方向朝考察区域平行移动.若经过n年，冰川的边界线P1P2移动的距离为s(km),并且s与n（n为正整数）的关系是.以O为原点，建立如图所示的平面直角坐标系，其中P1、P2的坐标分别是（-4，9）、（-13，-3）.‎ ‎（1）求线段P1P2所在的直线对应的函数关系式；‎ ‎（2）求冰川的边界线移动到考察区域所需要的最短时间.‎ ‎【题8】如图，平面直角坐标系xOy中，一次函数y=﹣x+b（b为常数，b＞0）的图象与x轴、y轴分别相交于点A、B，半径为4的⊙O与x轴正半轴相交于点C，与y轴相交于点D、E，点D在点E上方．‎ ‎（1）若直线AB与有两个交点F、G．‎ ‎①求∠CFE的度数；‎ ‎②用含b的代数式表示FG2，并直接写出b的取值范围；‎ ‎（2）设b≥5，在线段AB上是否存在点P，使∠CPE=45°？若存在，请求出P点坐标；若不存在，请说明理由．‎