2019年长春市中考数学试卷-2019带答案解析 23页

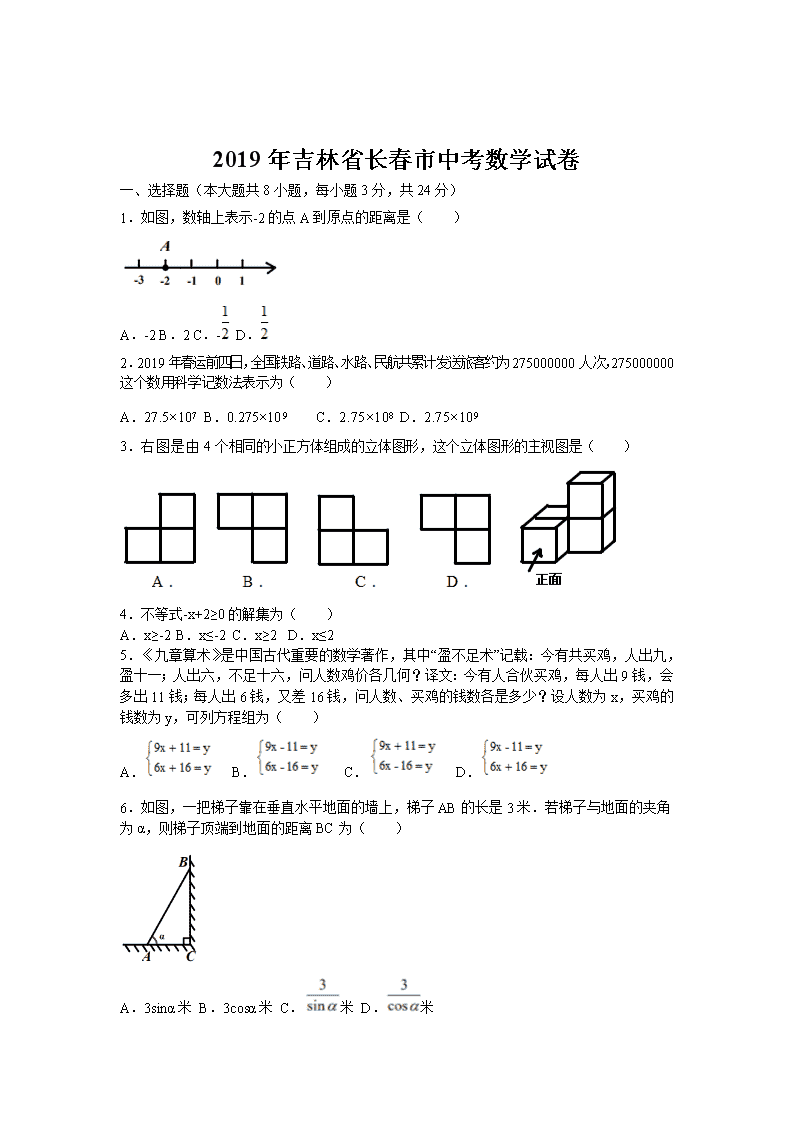
‎2019年吉林省长春市中考数学试卷 一、选择题（本大题共8小题，每小题3分，共24分）‎ ‎1．如图，数轴上表示-2的点A到原点的距离是（　　）‎ A．-2 B．2 C．- D．‎ ‎2．2019年春运前四日，全国铁路、道路、水路、民航共累计发送旅客约为275000000人次，275000000这个数用科学记数法表示为（　　）‎ A．27.5×107 B．0.275×109 C．2.75×108 D．2.75×109‎ ‎3．右图是由4个相同的小正方体组成的立体图形，这个立体图形的主视图是（　　）‎ ‎4．不等式-x+2≥0的解集为（　　）‎ A．x≥-2 B．x≤-2 C．x≥2 D．x≤2‎ ‎5．《九章算术》是中国古代重要的数学著作，其中“盈不足术”记载：今有共买鸡，人出九，盈十一；人出六，不足十六，问人数鸡价各几何？译文：今有人合伙买鸡，每人出9钱，会多出11钱；每人出6钱，又差16钱，问人数、买鸡的钱数各是多少？设人数为x，买鸡的钱数为y，可列方程组为（　　）‎ A． B． C． D．‎ ‎6．如图，一把梯子靠在垂直水平地面的墙上，梯子AB的长是3米．若梯子与地面的夹角为α，则梯子顶端到地面的距离BC为（　　）‎ A．3sinα米 B．3cosα米 C．米 D．米 ‎7．如图，在△ABC中，∠ACB为钝角．用直尺和圆规在边AB上确定一点D．使∠ADC=2∠B，则符合要求的作图痕迹是（　　）‎ ‎8．如图，在平面直角坐标系中，Rt△ABC的顶点A、C的坐标分别为（0，3）、（3，0）．∠ACB=90°，AC=2BC，函数y=（k＞0，x＞0）的图象经过点B，则k的值为（　　）‎ A． B．9 C． D．‎ 二、填空题（本大题共6小题，每小题3分，共18分）‎ ‎9．计算：3-=　 　‎ ‎10．分解因式：ab+2b=　 　‎ ‎11．一元二次方程x2-3x+1=0根的判别式的值为　 　．‎ ‎12．如图，直线MN∥PQ，点A、B分别在MN、PQ上，∠MAB=33°．过线段AB上的点C作CD⊥AB交PQ于点D，则∠CDB的大小为　 　度．‎ ‎13．如图，有一张矩形纸片ABCD，AB=8，AD=6．先将矩形纸片ABCD折叠，使边AD落在边AB上，点D落在点E处，折痕为AF；再将△AEF沿EF翻折，AF与BC相交于点G，则△GCF的周长为　 　‎ ‎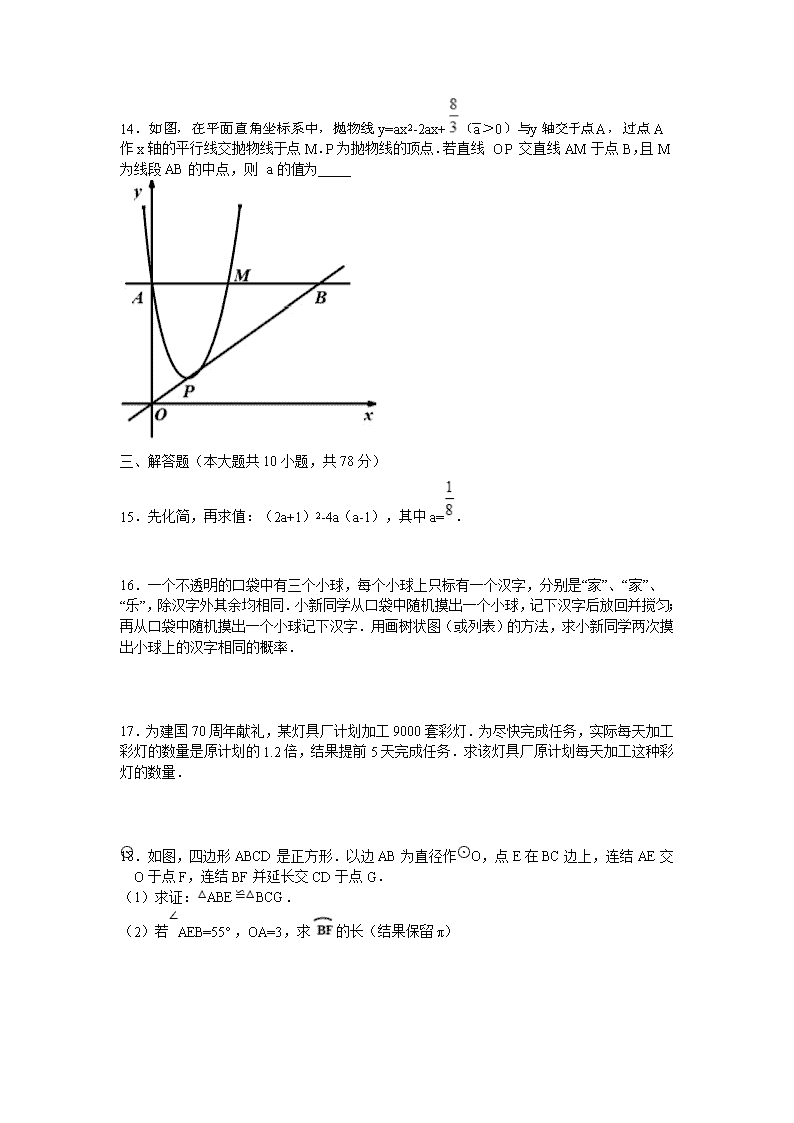14．如图，在平面直角坐标系中，抛物线y=ax2-2ax+（a＞0）与y轴交于点A，过点A作x轴的平行线交抛物线于点M．P为抛物线的顶点．若直线OP交直线AM于点B，且M为线段AB的中点，则a的值为　 　‎ 三、解答题（本大题共10小题，共78分）‎ ‎15．先化简，再求值：（2a+1）2-4a（a-1），其中a=．‎ ‎16．一个不透明的口袋中有三个小球，每个小球上只标有一个汉字，分别是“家”、“家”、“乐”，除汉字外其余均相同．小新同学从口袋中随机摸出一个小球，记下汉字后放回并搅匀；再从口袋中随机摸出一个小球记下汉字．用画树状图（或列表）的方法，求小新同学两次摸出小球上的汉字相同的概率．‎ ‎17．为建国70周年献礼，某灯具厂计划加工9000套彩灯．为尽快完成任务，实际每天加工彩灯的数量是原计划的1.2倍，结果提前5天完成任务．求该灯具厂原计划每天加工这种彩灯的数量．‎ ‎18．如图，四边形ABCD是正方形．以边AB为直径作⊙O，点E在BC边上，连结AE交⊙O于点F，连结BF并延长交CD于点G．‎ ‎（1）求证：△ABE≌△BCG．‎ ‎（2）若∠AEB=55°，OA=3，求的长（结果保留π）‎ ‎19．网上学习越来越受到学生的喜爱．某校信息小组为了解七年级学生网上学习的情况，从该校七年级随机抽取20名学生，进行了每周网上学习时间的调查，数据如下（单位：时）：‎ ‎3 2.5 0.6 1.5 1 2 2 3.3 2.5 1.8 2.5 2.2 3.5 4 1.5 2.5 3.1 2.8 3.3 2.4‎ 整理上面的数据，得到表格如下：‎ 样本数据的平均数、中位数、众数如下表所示：‎ 根据以上信息，解答下列问题：‎ ‎（1）上表中的中位数m的值为　 　，众数n的值为　 　‎ ‎（2）用样本中的平均数估计该校七年级学生平均每人一学期（按18周计算）网上学习的时间 ‎（3）已知该校七年级有200名学生，估计每周网上学习时间超过2小时的学生人数．‎ ‎20．图①、图②、图③均是6×6的正方形网格，每个小正方形的顶点称为格点，小正方形的边长为1，点A、B、C、D、E、F均在格点上．在图①、图②、图③中，只用无刻度的直尺，在给定的网格中按要求画图，所画图形的顶点均在格点上，不要求写出画法．‎ ‎（1）在图①中以线段AB为边画一个△ABM，使其面积为6．‎ ‎（2）在图②中以线段CD为边画一个△CDN，使其面积为6．‎ ‎（3）在图③中以线段EF为边画一个四边形EFGH，使其面积为9，且∠EFG=90°．‎ ‎21．已知A、B两地之间有一条长270千米的公路．甲、乙两车同时出发，甲车以60千米/时的速度沿此公路从A地匀速开往B地，乙车从B地沿此公路匀速开往A地，两车分别到达目的地后停止．甲、乙两车相距的路程y（千米）与甲车的行驶时间x（时）之间的函数关系如图所示．‎ ‎（1）乙车的速度为　 　千米/时，a=　 　，b=　 　‎ ‎（2）求甲、乙两车相遇后y与x之间的函数关系式．‎ ‎（3）当甲车到达距B地70千米处时，求甲、乙两车之间的路程．‎ ‎22．教材呈现：下图是华师版九年级上册数学教材第78页的部分内空．‎ 例2如图23.4.4，在△ABC中，D、E分别是边BC、AB的中点，AD，CE相交于点G．求证：‎ 证明：连结ED．‎ 请根据教材提示，结合图①，写出完事的证明过程．‎ 结论应用：‎ 在中，对角线AC、BD交于点O，E为边BC的中点，AE、BD交于点F．‎ ‎（1）如图②，若为正方形，且AB=6，则OF的长为　 　‎ ‎（2）如图③，连结DE交AC于点G．若四边形OFEG的面积为，则的面积为　 　‎ ‎23．如图，在Rt△ABC中，∠C=90°，AC=20，BC=15．点P从点A出发，沿AC向终点C运动，同时点Q从点C出发，沿射线CB运动，它们的速度均为每秒5个单位长度，点P到达终点时，P、Q同时停止运动．当点P不与点A、C重合时，过点P作PN⊥AB于点N，连结PQ，以PN、PQ为邻边作PQMN．设PQMN与△ABC重叠部分图形的面积为S．点P的运动时间为t秒．‎ ‎（1）①AB的长为　 　‎ ‎②PN的长用含t的代数式表示为　 　‎ ‎（2）当PQMN为矩形时，求t的值．‎ ‎（3）当PQMN与△ABC重叠部分图形为四边形时，求S与t之间的函数关系式．‎ ‎（4）当过点P且平行于BC的直线经PQMN一边中点时，直接写出t的值．‎ ‎24．已知函数y=‎ ‎（1）当n=5，‎ ‎①点P（4，b）在此函数图象上，求b的值．‎ ‎②求此函数的最大值．‎ ‎（2）已知线段AB的两个端点坐标分别为A（2，2）、B（4，2），当此函数的图象与线段AB只有一个交点时，直接写出n的取值范围．‎ ‎（3）当此函数图象上有4个点到x轴的距离等于4时，求n的取值范围．‎ ‎2019年吉林省长春市中考数学试卷 参考答案与试题解析 一、选择题（本大题共8小题，每小题3分，共24分）‎ ‎1．如图，数轴上表示-2的点A到原点的距离是（　　）‎ A．-2 B．2 C．- D．‎ 解：数轴上点A表示数为-2，-2到原点距离为2‎ 故选B ‎2．2019年春运前四日，全国铁路、道路、水路、民航共累计发送旅客约为275000000人次，275000000这个数用科学记数法表示为（　　）‎ A．27.5×107 B．0.275×109 C．2.75×108 D．2.75×109‎ 解：科学记数法为：把一个数表示成a与10的n次幂的相乘的形式（1≤a＜10，n为整数），故275000000用科学记数法表示为2.75×108‎ 故选C ‎3．右图是由4个相同的小正方体组成的立体图形，这个立体图形的主视图是（　　）‎ 解：如图所示，主视观看第二列有两个正方形，第一列右上有一个正方形，故观察为．‎ 故选A．‎ ‎4．不等式-x+2≥0的解集为（　　）‎ A．x≥-2 B．x≤-2 C．x≥2 D．x≤2‎ 解：解不等式-x+2≥0，移项可得-x≥-2，再系数化1，两边同时除以-1（注意改变不等号方向），得x≤2，‎ 故选D．‎ ‎5．《九章算术》是中国古代重要的数学著作，其中“盈不足术”记载：今有共买鸡，人出九，盈十一；人出六，不足十六，问人数鸡价各几何？译文：今有人合伙买鸡，每人出9钱，会多出11钱；每人出6钱，又差16钱，问人数、买鸡的钱数各是多少？设人数为x，买鸡的钱数为y，可列方程组为（　　）‎ A． B． C． D．‎ 解：根据题意，人数为x，鸡的钱数为y，当每人出9钱时，多出11钱，则可列方程9x-11=y，当每人出6钱时，差16钱，则可列方程6x+16=y，则解x，y可列方程组为．‎ 故选D ‎6．如图，一把梯子靠在垂直水平地面的墙上，梯子AB的长是3米．若梯子与地面的夹角为α，则梯子顶端到地面的距离BC为（　　）‎ A．3sinα米 B．3cosα米 C．米 D．米 解：如图所示：‎ α对应角为∠BAC，则sinα=，已知AB=3米，则BC=sinα，AB=3sinα米 故选A ‎7．如图，在△ABC中，∠ACB为钝角．用直尺和圆规在边AB上确定一点D．使∠ADC=2∠B，则符合要求的作图痕迹是（　　）‎ 解：由题意作图∠ADC=2∠B A、作图痕迹，为点D在线段AC垂直平分线上，能使∠A=∠ACD，不能使∠ADC=2∠B，故舍掉；‎ B、作图痕迹为点D在线段BC垂直平分线上，能使∠B=∠DCB，如图∠B+∠DCB=∠ACD，∴∠ADC=2∠B C、作图痕迹为点D为AB中点，故不能使∠ADC=2∠B（舍）D选项（舍）‎ 故选B ‎8．如图，在平面直角坐标系中，Rt△ABC的顶点A、C的坐标分别为（0，3）、（3，0）．∠ACB=90°，AC=2BC，函数y=（k＞0，x＞0）的图象经过点B，则k的值为（　　）‎ A． B．9 C． D．‎ 解：如图所示，‎ AC坐标分别为（0，3），（3，0）‎ 故∠AOC为等腰直角三角形∠ACO=45°，‎ ‎∴∠ACB=45°，‎ 过点B作BD⊥x轴，交x轴于点D，‎ ‎∴∠BDC=90°，∠CBD=45°，‎ ‎∴∠BDC为等腰直角三角形，‎ ‎∴∠AOC=∠BDC，∠ACO=∠BCD ‎∴△AOC∽△BDC ‎∴=‎ 又∵AC=2BC，‎ ‎∴AO=2BD ‎∴BD=‎ ‎∴CO=‎ ‎∴D坐标为（，0），B坐标为（，）‎ ‎∵点B在函数y=（k＞0，x＞0）图象上将点B坐标（，）代入y=中，得k=，‎ 故选D．‎ 二、填空题（本大题共6小题，每小题3分，共18分）‎ ‎9．计算：3-=　 　‎ 解：根据二次根式加减法则 故答案为：2．‎ ‎10．分解因式：ab+2b=　 　‎ 解：利用乘法结合律，提取出b，得b（a+2）‎ 故答案为：b（a+2）‎ ‎11．一元二次方程x2-3x+1=0根的判别式的值为　 　．‎ 解：∵a=1，b=﹣3，c=1，‎ ‎∴△=b2﹣4ac=（﹣3）2﹣4×1×1=5，‎ 故答案为：5．‎ ‎12．如图，直线MN∥PQ，点A、B分别在MN、PQ上，∠MAB=33°．过线段AB上的点C作CD⊥AB交PQ于点D，则∠CDB的大小为　 　度．‎ 解：∵MN∥PQ ‎∴∠ABD=∠MAB=33°‎ ‎∵CD⊥AB ‎∴∠DCB=90°‎ ‎∴∠ABD+∠CDB=180°-90°=90°‎ ‎∴∠CDB=90°-33°=57°‎ 故答案为：57°‎ ‎13．如图，有一张矩形纸片ABCD，AB=8，AD=6．先将矩形纸片ABCD折叠，使边AD落在边AB上，点D落在点E处，折痕为AF；再将△AEF沿EF翻折，AF与BC相交于点G，则△GCF的周长为　 　‎ 解：由图可知，FC=EB=AB-AD=8-6=2，∠CFG=45°‎ ‎∴GC=FC=2，∴FG=FC=2‎ ‎∴△GCF周长为2+2+2=4+2；‎ 故答案为：4+2‎ ‎14．如图，在平面直角坐标系中，抛物线y=ax2-2ax+（a＞0）与y轴交于点A，过点A作x轴的平行线交抛物线于点M．P为抛物线的顶点．若直线OP交直线AM于点B，且M为线段AB的中点，则a的值为　 　‎ 解：将x=0代入原式得y=，∴A（0，）‎ 将y=代入得ax2-2ax+=，ax2-2ax=0，x=2．‎ ‎∴M（2，）‎ ‎∵M为线段AB中点，‎ ‎∴B（4，）代入y=kx中求得OB解析式为y=x，‎ 将x=1代入得P（1，）将P代入抛物线解析式中得a=2．‎ 故答案为：2．‎ 三、解答题（本大题共10小题，共78分）‎ ‎15．先化简，再求值：（2a+1）2-4a（a-1），其中a=．‎ 解：原式=4a2+4a+1-4a2+4a=8a+1‎ 将a=代入原式=×8+1=2‎ ‎16．一个不透明的口袋中有三个小球，每个小球上只标有一个汉字，分别是“家”、“家”、“乐”，除汉字外其余均相同．小新同学从口袋中随机摸出一个小球，记下汉字后放回并搅匀；再从口袋中随机摸出一个小球记下汉字．用画树状图（或列表）的方法，求小新同学两次摸出小球上的汉字相同的概率．‎ 解：树状图如下：‎ 两次摸出相同小球的情况共有5种，故答案为 ‎17．为建国70周年献礼，某灯具厂计划加工9000套彩灯．为尽快完成任务，实际每天加工彩灯的数量是原计划的1.2倍，结果提前5天完成任务．求该灯具厂原计划每天加工这种彩灯的数量．‎ 解：设原计划每天加工这种彩灯x套，则实际每天加工这种彩灯1.2x套 ‎+5‎ ‎=5‎ ‎1800=6x x=300‎ 经检验x=300是方程的根．‎ 答：原计划每天加工这种彩灯300套．‎ ‎18．如图，四边形ABCD是正方形．以边AB为直径作⊙O，点E在BC边上，连结AE交⊙O于点F，连结BF并延长交CD于点G．‎ ‎（1）求证：△ABE≌△BCG．‎ ‎（2）若∠AEB=55°，OA=3，求的长（结果保留π）‎ ‎（1）证明：∵F在圆上，∴AF⊥BF，∠BAF+∠ABF=90°，∠ABF+∠CBF=90°‎ ‎∴∠BAF+=∠CBF，∵∠FBE+∠FEB=90°，∠FBE+∠BGC=90°‎ ‎∴∠FEB=∠BGC，在△ABE和△BGC中 ‎∴△ABE≌△BCE（ASA）‎ ‎（2）解：连接OF，‎ 则OF=OB，由（1）可得∠ABF=∠AEB=∠BGC=55°‎ ‎∴∠BFO=55°，∠BOF=70°‎ ‎∴=×2π×3=π ‎19．网上学习越来越受到学生的喜爱．某校信息小组为了解七年级学生网上学习的情况，从该校七年级随机抽取20名学生，进行了每周网上学习时间的调查，数据如下（单位：时）：‎ ‎3 2.5 0.6 1.5 1 2 2 3.3 2.5 1.8 2.5 2.2 3.5 4 1.5 2.5 3.1 2.8 3.3 2.4‎ 整理上面的数据，得到表格如下：‎ 样本数据的平均数、中位数、众数如下表所示：‎ 根据以上信息，解答下列问题：‎ ‎（1）上表中的中位数m的值为　 　，众数n的值为　 　‎ ‎（2）用样本中的平均数估计该校七年级学生平均每人一学期（按18周计算）网上学习的时间 ‎（3）已知该校七年级有200名学生，估计每周网上学习时间超过2小时的学生人数．‎ 解：将调查数据由小到大排列为：0.6，1，1.5，1.5，1.8，2，2，2.2，2.4，2.5，2.5，2.5，2.5，2.8，3，3.1，3.3,3.3，3.5，4．‎ ‎（1）则中位数m为第10与,11两个数的平均数为=2.5，众数n为出现最多的数为2.5．‎ ‎（2）由题中表格可知平均数为2.4，即该校七年级学生平均每人一周网上学习时间为2.4小时，则平均每人一学期学生时间为2.4×18=43.2时．‎ ‎（3）由调查可知，每周上网学习超过2小时的学生占=，则200名学生中每周上网超过2小时的学生人数估计为200×=130人．‎ 故答案为：（1）2.5；2.5．‎ ‎20．图①、图②、图③均是6×6的正方形网格，每个小正方形的顶点称为格点，小正方形的边长为1，点A、B、C、D、E、F均在格点上．在图①、图②、图③中，只用无刻度的直尺，在给定的网格中按要求画图，所画图形的顶点均在格点上，不要求写出画法．‎ ‎（1）在图①中以线段AB为边画一个△ABM，使其面积为6．‎ ‎（2）在图②中以线段CD为边画一个△CDN，使其面积为6．‎ ‎（3）在图③中以线段EF为边画一个四边形EFGH，使其面积为9，且∠EFG=90°．‎ 解：（1）因小正方形边长为1，已知AB=3，则要使△ABM面积为6，只要以AB为底，高为4即可，如图，M在直线NP上任意一点均可．‎ ‎（2）CD竖向距离为3，可看为以水平方向为底，竖直方向为高的三角形一边，高为3，当底为4时，面积就为6，如图（答案不唯一）‎ ‎（3）以线段EF为边画一个四边形，使其面积为9，我们已知最规则面积为9的四边形是边长为3的正方形，但E、F不是网格上的边，我们可用割补法来求出我们想要图形，如图所示，S△FGI=S△EJF，则S四边形EFGH=S四边形JFIH=9‎ ‎21．已知A、B两地之间有一条长270千米的公路．甲、乙两车同时出发，甲车以60千米/时的速度沿此公路从A地匀速开往B地，乙车从B地沿此公路匀速开往A地，两车分别到达目的地后停止．甲、乙两车相距的路程y（千米）与甲车的行驶时间x（时）之间的函数关系如图所示．‎ ‎（1）乙车的速度为　 　千米/时，a=　 　，b=　 　‎ ‎（2）求甲、乙两车相遇后y与x之间的函数关系式．‎ ‎（3）当甲车到达距B地70千米处时，求甲、乙两车之间的路程．‎ 解：（1）共270千米，2小时两车相遇，即两车共走270千米，V总=270÷2=135（km/h）‎ ‎∵V甲=60km/h，∴V2=V总-V甲=135-60=75km/h a点为乙车到A地时的时间，即t乙==270÷75=3.6‎ b点为甲车到B地的时间，即t甲==270÷60=4.5‎ ‎（2）设函数关系式为y=kx+b，当2＜x≤3.6时，斜率k为两车速度和135‎ ‎∴y=135x+b，又有x=2时，y=0，∴b=-270，∴y=135x-270‎ 当3.6＜x≤4.5时，斜率k为甲车速度为60，∴y=60x+b，‎ 又有x=4.5时，y=270，∴b=0，∴y=60x，‎ 综上所述，‎ ‎（3）甲距B地70千米处时，t==，当x=时，y=135×-270=180km ‎∴甲乙两车之间路程为180千米．‎ 故答案为：（1）75；3.6；4.5‎ ‎22．教材呈现：下图是华师版九年级上册数学教材第78页的部分内空．‎ 例2如图23.4.4，在△ABC中，D、E分别是边BC、AB的中点，AD，CE相交于点G．求证：‎ 证明：连结ED．‎ 请根据教材提示，结合图①，写出完事的证明过程．‎ 结论应用：‎ 在中，对角线AC、BD交于点O，E为边BC的中点，AE、BD交于点F．‎ ‎（1）如图②，若为正方形，且AB=6，则OF的长为　 　‎ ‎（2）如图③，连结DE交AC于点G．若四边形OFEG的面积为，则的面积为　 　‎ 解：教材呈现：连接ED ‎∵E、D分别为AB、BC中点 ‎∴E、D为三角形AB的中位线 ‎∴ED∥AC，且ED=AC，而由于ED∥AC ‎∴∠DEC=∠ECA 又∠EGD=∠AGC ‎∴△EGD∽△CGA ‎∴‎ 又EC=EG+GC，AD=AG+AD ‎∴‎ 结论应用：（1）在△ABC中，O为AC中点，E为BC中点，故在△ABC中，F点为中线的交点，即，而AB=AC=6，故AC=6，BO=3，OF=‎ ‎（2）连接OE，OE为△OBC中线，故S△OBE=S△OEC，在△ABC中，可得OF=OB，而在△OEB中，由于△OEB与△OEF等高，故S△OFE：S△OEB=OF：OB=1：3‎ 同理S△OGE：S△OEC=1：3，故S△FEG：S△OBC=1：3，故S△FEG：SABCD=1：12‎ 故SABCD=×12=6‎ 故答案为：（1）；（2）6‎ ‎23．如图，在Rt△ABC中，∠C=90°，AC=20，BC=15．点P从点A出发，沿AC向终点C运动，同时点Q从点C出发，沿射线CB运动，它们的速度均为每秒5个单位长度，点P到达终点时，P、Q同时停止运动．当点P不与点A、C重合时，过点P作PN⊥AB于点N，连结PQ，以PN、PQ为邻边作PQMN．设PQMN与△ABC重叠部分图形的面积为S．点P的运动时间为t秒．‎ ‎（1）①AB的长为　 　‎ ‎②PN的长用含t的代数式表示为　 　‎ ‎（2）当PQMN为矩形时，求t的值．‎ ‎（3）当PQMN与△ABC重叠部分图形为四边形时，求S与t之间的函数关系式．‎ ‎（4）当过点P且平行于BC的直线经PQMN一边中点时，直接写出t的值．‎ 解：（1）①由于△ABC为直角三角形，由勾股定理得AB==25‎ ‎②由于PN⊥AB，故∠PNA=90°=∠C，即∠A=∠A，故△ANP∽△ACB 故∴PN=3t ‎（2）由于PNMQ为矩形，PN⊥NM，故M点落在AB上，而PN=4t，△QBM∽△ABC，故 QM=（15-5t）‎ QM=PN得t=‎ ‎（3）‎ 在运动过程中，起始为PNQM的平行四边形是阴影部分（图一）后，M总落在AB上，形成矩形，后M总落在三角形处，阴影部分为梯形（图二），后Q达到B点继续移动，阴影部分为三角形（图三），而题意及（2）得分总为t=和t=3，求前两种 ‎①当0＜t＜时，以PN为底，延长QM与O，NO为高，由PN=3t，PA=5t，∴AN=4t，而△QOB∽△ACB，故QB=（15-5t），OB=（15-5t）‎ S=PN·NO=PN×（AB-AN-OB）=3t×[25-4t-（15-5t）]=48t-3t2‎ 当＜t＜3时，设QM与AB交于O，QO=（15-5t）‎ S=（PN+QO）×NO=[×5t+（15-5t）]×[25-4t-（15-5t）]‎ ‎=（16-t）（12-t）=-14t+96‎ ‎（4）‎ 作PH∥CB，则H可能在NM上或QM上 当H在NM上，则NH=HM，过N作NR∥CB，MS∥BC 设PS=a，设SM与PQ交点为O，易得O为RQ中点，‎ 由平行线等分线段定理得，RP=RS=SC=a 而NR∥CB，∴NR⊥AC，易得△RPN∽△NPN；‎ ‎△ARN∽△ANP，∴AR=a，而 解得t=＜4成立 当H在QM上，则QH=HM，设RS=a，由上一种情况，我们得到RS=SP=PC=a，在△PRM中，RN=a，故AP=a ‎∴‎ ‎∴t=＜4成立 故答案为：（1）①25；②3t．‎ ‎24．已知函数y=‎ ‎（1）当n=5，‎ ‎①点P（4，b）在此函数图象上，求b的值．‎ ‎②求此函数的最大值．‎ ‎（2）已知线段AB的两个端点坐标分别为A（2，2）、B（4，2），当此函数的图象与线段AB只有一个交点时，直接写出n的取值范围．‎ ‎（3）当此函数图象上有4个点到x轴的距离等于4时，求n的取值范围．‎ 解：（1）当n=5时，y=‎ ‎①由于4＜5，故b=（-42+5×4+5）=‎ ‎②y=‎ 当x≥5时，x=5最大y=5‎ 当x＜5时，x=最大y=＞5，故最大值为 ‎（2）①首先以A点为边界，设当x≥n时的图形如α 当x＜n时为β 如图一：此时函数图象与线段AB恰好有一个交点，交点在α上，随着n的不断增大，图象逐渐右移直至β与B相交．‎ 如图二，将（2，2）分别代入α，β得n=2，n=．图一情况下，恰有一个交点，所以n可以取到2，而图二情况下，恰有两个交点，故n不能取到 综上2≤n＜‎ ‎②n从图二的情况开始继续不断增大的一段时间内函数图象与线段一直有两个交点，直到如图三，此时β与线段有一个交点，而α刚要离开线段．在此之后直至运动至图四情况．β刚要离开线段AB在此期间之内，函数图象与线段AB一直只有一个交点，‎ 图三中将（4，2）代入α得n=，‎ 图四中将（4，2）代入β得n=4，注意图三时恰有两个交点，因此n＞，而在图四情况下，恰有一个交点，故n≤4‎ 综上＜n≤4．‎ 综上所述n的取值范围是2≤n＜或＜n≤4．‎ ‎（3）当有4个点到x轴的距离等于4，即函数图象与直线y=4和直线y=-4恰有四个交点．‎ ‎①设x＜n时图象为β，x≥n时图象为α．‎ 当n很小时函数图象与y=±4一直有4个交点，不断增大n，直到如图五情况，此时β刚要经过y=-4，之后的一段时间内，函数与y=±4有5个交点，此时n2+·n+=-4，n=-8故n≤-8时恒成立．‎ ‎②在图五之后的一段时间内，函数与y=±4共有5个交点．直到运动到图六情况α的顶点落在y=4上，即+n=4，∴n=-2-2（舍n＞0解）‎