核按钮2015高考新课标数学理课时作业101算法与程序框图 5页

‎10.1　算法与程序框图 ‎1．在算法的逻辑结构中，要求进行逻辑判断，并根据结果进行不同处理的是哪种结构(　　)‎ A．顺序结构 ‎ B．条件结构和循环结构 C．顺序结构和条件结构 ‎ D．没有任何结构 解：条件结构要进行逻辑判断，而循环结构中含有条件结构．故选B.‎ ‎2．如图的程序框图输出的结果是(　　)‎ A．4 B．‎3 ‎ C．2 D．0‎ 解：该算法首先将1，2，3三个数分别赋给x，y，z；然后先让x取y的值，即x变成2，再让y取x的值，即y的值是2，接着让z取y的值，即z的值为2，从而最后输出z的值为2.故选C.‎ ‎3．()执行如图的程序框图，如果输入的t∈[－1，3]，则输出的s的取值范围为(　　)‎ A. B. C. D. 解：由框图知s＝当－1≤t<1时，－3≤s<3；当1≤t≤3时，3≤s≤4.综上，－3≤s≤4.故选A.‎ ‎4．()如图，阅读程序框图，运行相应的程序，当输入x的值为－25时，输出x的值为(　　)‎ A．－1 B．‎1 ‎ C．3 D．9‎ 解：初始值x＝－25.第一次循环得x＝4，第二次循环得x＝1，此时不满足判断框条件，退出循环，x＝2×1＋1＝3，输出x的值为3.故选C.‎ ‎5．()执行如图所示的程序框图，则输出的S值是(　　)‎ A．－1 B. C. D．4‎ 解：根据程序框图计算得S＝4，i＝1；S＝－1，i＝2；S＝，i＝3；S＝，i＝4；S＝4，i＝5，由此可知S的值呈周期出现，循环周期为4，所以i＝9时与i＝5时输出的值相同，故选D.‎ ‎6．()执行如图的程序框图，如果输入的N＝10，那么输出的S＝(　　)‎ A．1＋＋＋…＋ B．1＋＋＋…＋ C．1＋＋＋…＋ D．1＋＋＋…＋ 解：第一次循环，T＝1，S＝1，k＝2；第二次循环，T＝，S＝1＋，k＝3；第三次循环，T＝，S＝1＋＋，k＝4；…；第十次循环，T＝，S＝1＋＋＋…＋，k＝11>10，退出循环，输出的S＝1＋＋＋…＋.故选B.‎ ‎7．()阅读如图所示的程序框图，运行相应的程序，输出的结果i＝____________．‎ 解：初始值a＝10，i＝1.‎ 第一次循环得a＝5，i＝2；第二次循环得a＝16，i＝3；‎ 第三次循环得a＝8，i＝4；第四次循环得a＝4，i＝5，‎ 此时退出循环，输出i＝5.故填5.‎ ‎8．某城市缺水问题比较突出，为了制定节水管理办法，对全市居民某年的月均用水量进行了抽样调查，其中n位居民的月均用水量分别为x1，x2，…，xn(单位：吨)．根据如图所示的程序框图，若n＝2，且x1，x2分别为1，2，则输出的结果s为________．‎ 解：初始值s1＝0，s2＝0，i＝1.‎ 第一次循环得s1＝1，s2＝1，s＝0，i＝2；‎ 第二次循环得s1＝3，s2＝5，s＝0.25，i＝3，此时退出循环，输出s的值为0.25.故填0.25.‎ ‎9．一个人带着三只狼和三只羊过河，只有一条船，同时可容纳一个人和两只动物，没有人在的时候，如果狼的数量不少于羊的数量，狼就会吃羊．该人如何将动物转移过河？请设计算法．‎ 解：同种动物同船不用考虑动物的争斗但需考虑承载的数量，还应考虑到两岸的动物都得保证狼的数量要小于羊的数量，故在算法的构造过程中尽可能保证船里面有狼，这样才能使得两岸的羊的数量占到优势，具体算法如下：‎ 第一步：人带两只狼过河，并自己返回；‎ 第二步：人带一只狼过河，自己返回；‎ 第三步：人带两只羊过河，并带两只狼返回；‎ 第四步：人带一只羊过河，自己返回；‎ 第五步：人带两只狼过河．‎ ‎10．到银行办理个人异地汇款，银行收取一定的手续费，汇款额不超过100元，收取1元手续费；超过100元但不超过5 000元，按汇款额的1%收取；超过5 000元，一律收取50元手续费．试用条件语句描述汇款额为x元时，银行收取手续费y元的过程，画出流程图．‎ 解： 这是一个实际问题，故应先建立数学模型，‎ y＝ 由此看出，求手续费时，需先判断x的范围，故应用条件结构描述．流程图如图所示：‎ ‎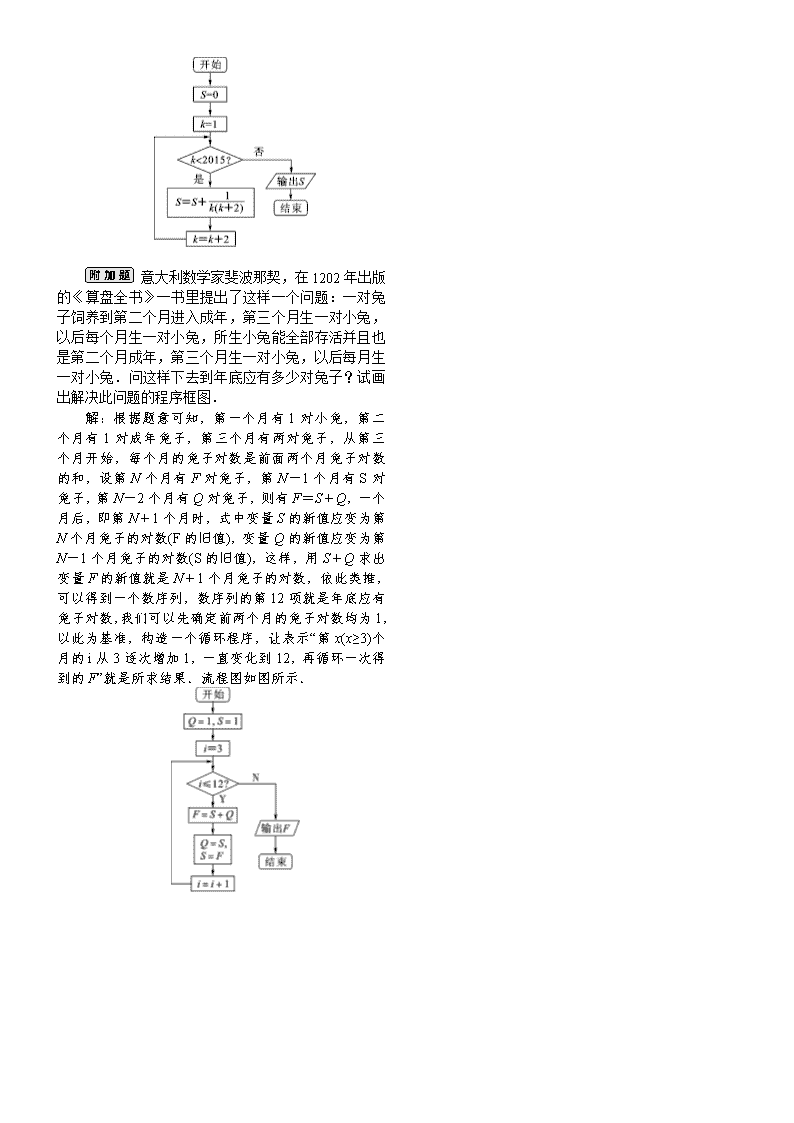11．设计一个算法计算＋＋＋…＋的值，并画出程序框图．‎ 解：算法步骤如下：‎ 第一步，令S＝0，k＝1.‎ 第二步，若k<2015成立，则执行第三步，否则输出S.‎ 第三步，计算S＝S＋，k＝k＋2，返回第二步．‎ 程序框图如图所示：‎ ‎ 意大利数学家斐波那契，在1202年出版的《算盘全书》一书里提出了这样一个问题：一对兔子饲养到第二个月进入成年，第三个月生一对小兔，以后每个月生一对小兔，所生小兔能全部存活并且也是第二个月成年，第三个月生一对小兔，以后每月生一对小兔．问这样下去到年底应有多少对兔子？试画出解决此问题的程序框图．‎ 解：根据题意可知，第一个月有1对小兔，第二个月有1对成年兔子，第三个月有两对兔子，从第三个月开始，每个月的兔子对数是前面两个月兔子对数的和，设第N个月有F对兔子，第N－1个月有S对兔子，第N－2个月有Q对兔子，则有F＝S＋Q，一个月后，即第N＋1个月时，式中变量S的新值应变为第N个月兔子的对数(F的旧值)，变量Q的新值应变为第N－1个月兔子的对数(S的旧值)，这样，用S＋Q求出变量F的新值就是N＋1个月兔子的对数，依此类推，可以得到一个数序列，数序列的第12项就是年底应有兔子对数，我们可以先确定前两个月的兔子对数均为1，以此为基准，构造一个循环程序，让表示“第x(x≥3)个月的i从3逐次增加1，一直变化到12，再循环一次得到的F”就是所求结果．流程图如图所示．‎