高考数学总复习指数函数对数函数及幂函数 8页

第二章　函数与导数第9课时　指数函数、对数函数及幂函数(3) (对应学生用书(文)、(理)24～25页)‎ 考情分析 考点新知 ‎① 对数函数在高考中的考查主要是图象和性质，同时考查数学思想方法，以考查分类讨论及运算能力为主；考查形式主要是填空题，同时也有综合性较强的解答题出现，目的是结合其他章节的知识，综合进行考查.‎ ‎② 幂函数的考查较为基础，以常见的5种幂函数为载体，考查求值、单调性、奇偶性、最值等问题是高考命题的出发点．‎ 理解对数函数的概念；理解对数函数的单调性；掌握对数函数图象通过的特殊点.‎ ‎② 知道对数函数是一类重要的函数模型.‎ ‎③ 了解指数函数y＝ax与对数函数y＝logax的相互关系(a>0，a≠1).‎ ‎④ 了解幂函数的概念，结合函数y＝x，y＝x2，y＝x3，y＝x－1，y＝x－2的图象，了解它们的变化情况.‎ ‎1. (必修1P112测试8改编)已知函数f(x)＝logax(a>0，a≠1)，若f(2)>f(3)，则实数a的取值范围是________．‎ 答案：(0，1)‎ 解析：因为f(2)>f(3)，所以f(x)＝logax单调递减，则a∈(0，1)．‎ ‎2. (必修1P89练习3改编)若幂函数y＝f(x)的图象经过点，则f(25)＝________．‎ 答案： 解析：设f(x)＝xα，则＝9α，∴ α＝－，即f(x)＝x－，f(25)＝.‎ ‎3. (必修1P111习题15改编)函数f(x)＝ln是________(填“奇”或“偶”)函数．‎ 答案：奇 解析：因为f(－x)＝ln＝ln＝－ln＝－f(x)，所以f(x)是奇函数．‎ ‎4. (必修1P87习题13改编)不等式lg(x－1)<1的解集为________. ‎ 答案：(1，11)‎ 解析：由00，a≠1)叫做对数函数，其中x是自变量，函数的定义域是(0，＋∞)．‎ ‎2. 对数函数的图象与性质 a>1‎ ‎00；当0＜x＜1时，f(x)<0‎ ‎(4) 当x＞1时，f(x)<0；当0＜x＜1时，f(x)>0‎ ‎(5) 是(0，＋∞)上的增函数 ‎(5) 是(0，＋∞)上的减函数 ‎3. 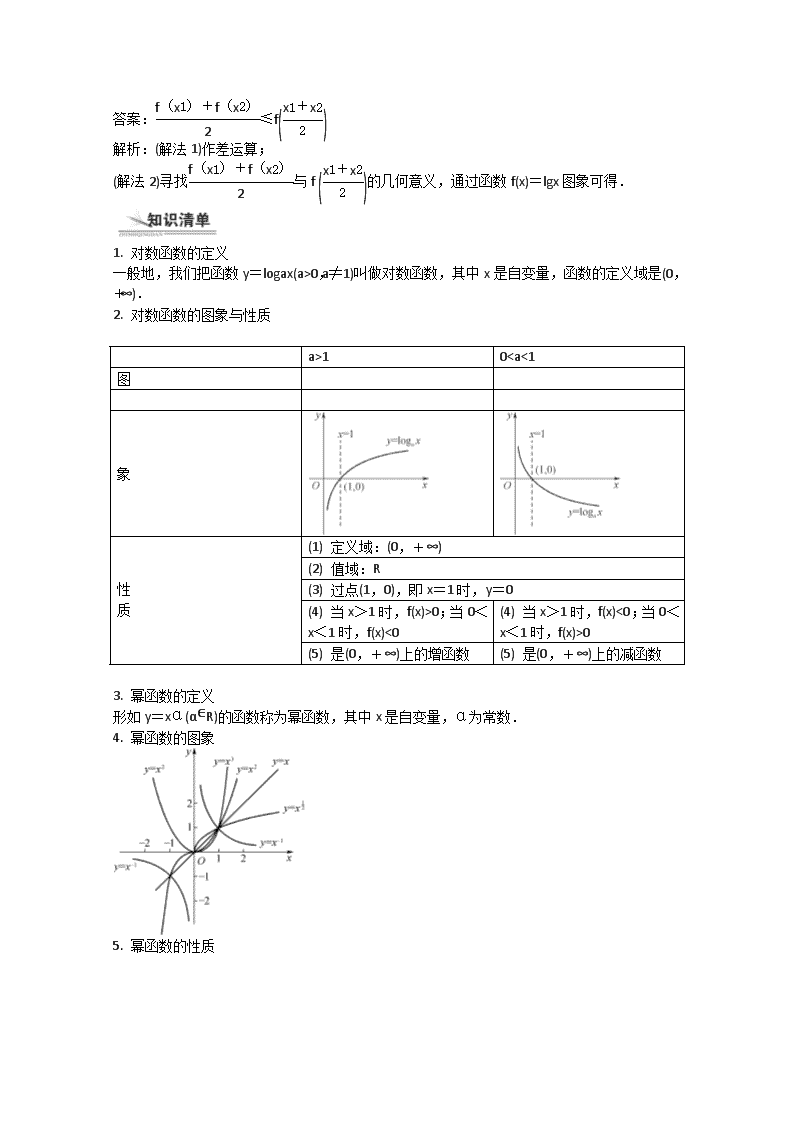幂函数的定义 形如y＝xα(α∈R)的函数称为幂函数，其中x是自变量，α为常数．‎ ‎4. 幂函数的图象 ‎5. 幂函数的性质 函数特 征性质 y＝x y＝x2‎ y＝x3‎ y＝x y＝x－1‎ 定义域 R R R ‎{x|x≥0}‎ ‎{x|x∈R且x≠0}‎ 值域 R ‎{y|y≥0}‎ R ‎{y|y≥0}‎ ‎{y|y∈R且y≠0}‎ 奇偶性 奇 偶 奇 非奇非偶 奇 单调性 增 ‎(－∞，0]减，‎ ‎[0，＋∞)增 增 增 ‎(－∞，0)减，(0，＋∞)减 定点 ‎(1，1)‎ ‎[备课札记]‎ 题型1　对数函数的概念与性质 例1　(1) 设a>1，函数f(x)＝logax在区间[a，2a]上的最大值与最小值之差是，则a＝________；‎ ‎(2) 若a＝log0.40.3，b＝log54，c＝log20.8，用小于号“<”将a、b、c连结起来________；‎ ‎(3) 设f(x)＝lg是奇函数，则使f(x)<0的x的取值范围是________；‎ ‎(4) 已知函数f(x)＝|log2x|，正实数m、n满足m1，∴ 函数f(x)＝logax在区间[a，2a]上是增函数，∴ loga2a－logaa＝，∴ a＝4.‎ ‎(2) 由于a>1，01，且mn＝1，所以f(m2)＝|log2m2|＝2，解得m＝，‎ 所以n＝2.‎ ‎(1) 设loga＜1，则实数a的取值范围是________；‎ ‎(2) 已知函数f(x)＝lg(x2＋t)的值域为R，则实数t的取值范围是________；‎ ‎(3) 若函数f(x)＝loga|x＋1|在(－1，0)上有f(x)>0，则函数f(x)的单调减区间是________；‎ ‎(4) 若函数f(x)＝log(x2－2ax＋3)在(－∞，1]内为增函数，则实数a的取值范围是________．‎ 答案：(1) 0＜a＜或a＞1　(2) a≤0　(3) (－1，＋∞)　(4) [1，2)‎ 解析：(1) 分a＞1与a＜1两种情形进行讨论．‎ ‎(2) 值域为R等价于x2＋a可以取一切正实数．‎ ‎(3) 函数f(x)的图象是由y＝loga|x|的图象向左平移1个单位得到，∴ 03－2a>0或0>a＋1>3－2a或a＋1<0<3－2a.‎ 解得a<－1或0，则方程(a－1)t2－at－1＝0有且只有一个正根．‎ ‎①a＝1t＝－，不合题意；②a≠1时，Δ＝0a＝或－3.若a＝t＝－2，不合题意，若a＝－3t＝；③a≠1时，Δ>0，一个正根与一个负根，即<0a>1.‎ 综上，实数a的取值范围是{－3}∪(1，＋∞)．‎ 已知函数f(x)＝lg(ax－bx)(a>1>b>0)．‎ ‎(1) 求函数y＝f(x)的定义域；‎ ‎(2) 在函数y＝f(x)的图象上是否存在不同的两点，使过此两点的直线平行于x轴；‎ ‎(3) 当a、b满足什么关系时，f(x)在区间上恒取正值．‎ 解：(1) 由ax－bx>0，得x>1，因为a>1>b>0，所以>1，所以x>0，即函数f(x)的定义域为(0，＋∞)．‎ ‎(2) 设x1>x2>0，因为a>1>b>0，所以ax1>ax2，bx1－bx2，所以ax1－bx1>ax2－bx2>0，于是lg(ax1－bx1)>lg(ax2－bx2)，即f(x1)>f(x2)，因此函数f(x)在区间(0，＋∞)上是增函数．假设函数y＝f(x)的图象上存在不同的两点A(x1，y1)、B(x2，y2)，使得直线AB平行于x轴，即x1≠x2，y1＝y2，这与f(x)是增函数矛盾．故函数y＝f(x)的图象上不存在不同的两点，使过此两点的直线平行于x轴．‎ ‎(3) 由(2)知，f(x)在区间(1，＋∞)上是增函数，所以当x∈(1，＋∞)时，f(x)>f(1)，故只需f(1)≥0，即lg(a－b)≥0，即a－b≥1，所以当a≥b＋1时，f(x)在区间(1，＋∞)上恒取正值．‎ ‎1. (2013·南师大模拟)已知函数f(x)＝log2x－2log2(x＋c)，其中c>0，若对任意x∈(0，＋∞)，都有f(x)≤1，则c的取值范围是________．‎ 答案：c≥ 解析：由题意，在x∈(0，＋∞)上恒成立，所以c≥.‎ ‎2. (2013·辽宁)已知函数f(x)＝ln＋1，则f(lg2)＋f＝________．‎ 答案：2‎ 解析：f(x)＋f(－x)＝ln(－3x)＋ln(＋3x)＋2＝ln(1＋9x2－9x2)＋2＝2，所以f(lg2)＋f＝f(lg2)＋f(－lg2)＝2.‎ ‎3. (2013·江西检测)已知x＋(log0.5)－y<(－y)＋(log0.5)x，则实数x、y的关系为________．‎ 答案：x＋y<0‎ 解析：由x＋(log0.5)－y<(－y)＋(log0.5)x，得x－(log0.5)x<(－y)－(log0.5)－y.设f(x)＝x－(log0.5)x，则f(x)0，由af2(x)≥f(x)－1，得a≥＝－＝－≤(当且仅当f(x)＝2时等号成立)，所以实数a的最小值为.‎ ‎1. 若函数f(x)＝log2|ax－1|(a＞0)，当x≠时，有f(x)＝f(1－x)，则a＝________．‎ 答案：2‎ 解析：由f(x)＝f(1－x)，知函数f(x)的图象关于x＝对称，‎ 而f(x)＝log2＋log2|a|，从而＝，所以a＝2.‎ ‎2. 已知函数f(x)＝x，x∈[－1，8]，函数g(x)＝ax＋2，x∈[－1，8]，若存在x∈[－1，8]，使f(x)＝g(x)成立，则实数a的取值范围是________．‎ 答案：∪[1，＋∞)‎ 解析：分别作出函数f(x)＝x，x∈[－1，8]与函数g(x)＝ax＋2，x∈[－1，8]的图象．当直线经过点(－1，1)时，a＝1；当直线经过点(8，4)时，a＝.结合图象有a≤或a≥1.‎ ‎3. 已知函数f(x)＝|lgx|，若0f(1) ＝1＋2＝3，即a＋2b的取值范围是(3，＋∞)．‎ ‎4. 已知两条直线l1：y＝m和l2：y＝，l1与函数y＝|log2x|的图象从左至右相交于点A、B，l2与函数y＝|log2x|的图象从左至右相交于点C、D.记线段AC和BD在x轴上的投影长度分别为a、b.当m变化时，求的最小值．‎ 解：由题意得xA＝m，xB＝2m，xC＝，xD＝2，所以a＝|xA－xC|＝，b＝|xB－xD|＝，即＝＝2·2m＝2＋m.‎ 因为＋m＝(2m＋1)＋－≥2－＝，当且仅当(2m＋1)＝‎ ，即m＝时取等号．所以，的最小值为2＝8.‎ ‎1. 指数函数的底数、对数函数的底数、真数应满足的条件，是求解有关指数、对数问题时必须予以重视的，如果底数含有参数，一般需分类讨论．‎ ‎2. 与对数函数有关的复合函数的单调性的求解步骤 ‎(1) 确定定义域；‎ ‎(2) 把复合函数分解为几个初等函数；‎ ‎(3) 确定各个基本初等函数的单调区间；‎ ‎(4) 根据“同增异减”判断复合函数的单调性．‎