2020高考数学一轮复习 函数系列之二次函数学案 6页

二次函数 一、教学目标：掌握二次函数的概念、图象及性质；能利用二次函数研究一元二次方程的实根分布条件；能求二次函数的区间最值．‎ 二、教学重点：‎ ‎1．二次函数的图象与性质、二次函数、二次方程与二次不等式的关系是重点，‎ ‎2．二次函数最值问题、一元二次方程根的分布及二次函数的图象性质灵活应用是难点。‎ 三、教学过程：‎ ‎（一）主要知识：‎ 一）正比例函数，一次函数，反比例函数 ‎1.正比例函数 ‎ ‎2.一次函数 其图象为一直线，时增函数，时减函数。而时为常数函数。‎ ‎3.反比例函数 定义域，值域，图象是双曲线，时在上递减，时在递增。‎ 二）二次函数 ‎1．二次函数的解析式的三种形式 ‎(1)一般式：f(x)=ax2+bx+c(a≠0)，其中a是开口方向与大小，c是Y轴上的截距，而是对称轴。‎ ‎(2)顶点式（配方式）：f(x)=a(x-h)2+k其中(h,k)是抛物线的顶点坐标。‎ ‎(3)两根式（因式分解）：f(x)=a(x-x1)(x-x2),其中x1,x2是抛物线与x轴两交点的坐标。‎ 求一个二次函数的解析式需三个独立条件，如：已知抛物线过三点，已知对称轴和两点，已知顶点和对称轴。又如，已知f(x)=ax2+bx+c(a≠0)，方程f(x)-x=0的两根为，则可设f(x)-x=或。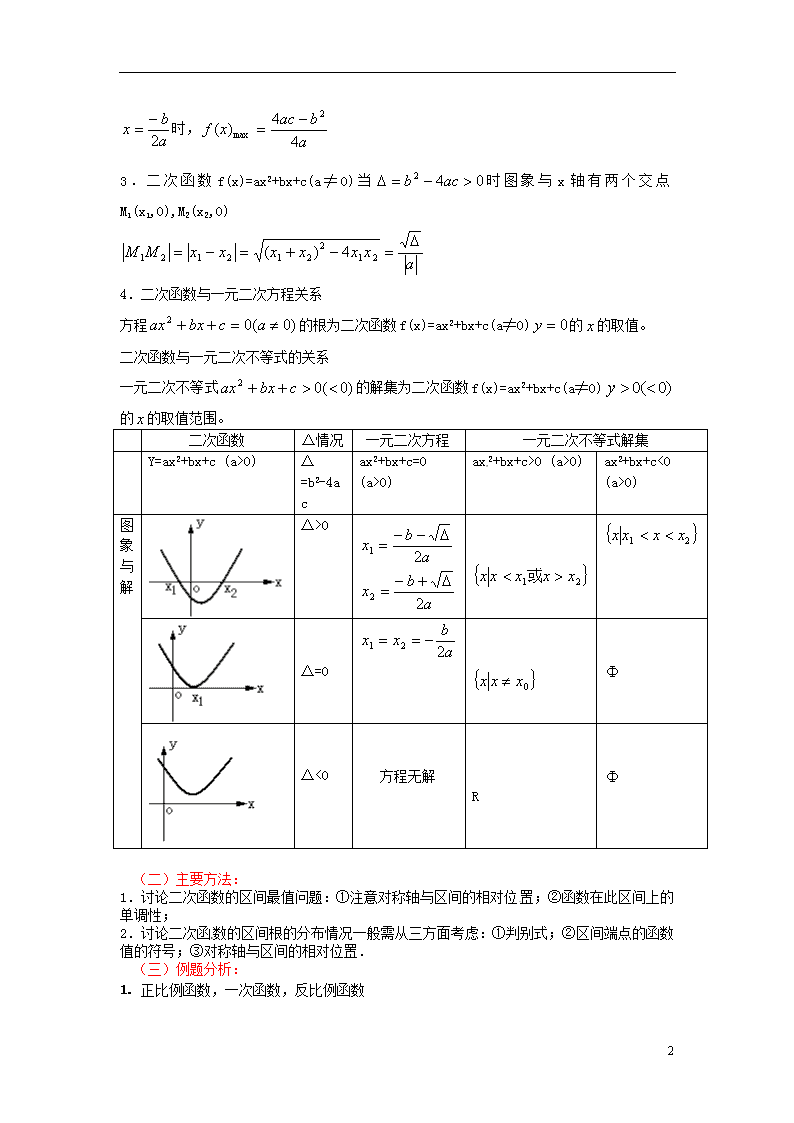‎ ‎2．二次函数f(x)=ax2+bx+c(a≠0)的图象是一条抛物线，对称轴，顶点坐标 ‎（1）a>0时，抛物线开口向上，函数在上单调递减，在上单调递增，时，‎ ‎（2）a<0时，抛物线开口向下，函数在上单调递增，在上单调递减，‎ 6‎ 时，‎ ‎3．二次函数f(x)=ax2+bx+c(a≠0)当时图象与x轴有两个交点M1(x1,0),M2(x2,0)‎ ‎4．二次函数与一元二次方程关系 方程的根为二次函数f(x)=ax2+bx+c(a≠0)的的取值。‎ 二次函数与一元二次不等式的关系 一元二次不等式的解集为二次函数f(x)=ax2+bx+c(a≠0)的的取值范围。‎ 二次函数 ‎△情况 一元二次方程 一元二次不等式解集 Y=ax2+bx+c (a>0)‎ ‎△=b2‎‎-4ac ax2+bx+c=0 (a>0)‎ ax2+bx+c>0 (a>0)‎ ax2+bx+c<0 (a>0)‎ 图象与解 ‎△>0‎ ‎△=0‎ ‎△<0‎ 方程无解 R ‎（二）主要方法：‎ ‎1．讨论二次函数的区间最值问题：①注意对称轴与区间的相对位置；②函数在此区间上的单调性； ‎ ‎2．讨论二次函数的区间根的分布情况一般需从三方面考虑：①判别式；②区间端点的函数值的符号；③对称轴与区间的相对位置．‎ ‎（三）例题分析：‎ ‎1. 正比例函数，一次函数，反比例函数 6‎ 例1 作函数的图象，并指出函数的定义域、值域，单调区间，对称轴、对称中心及顶点坐标。‎ 分析： 先通过图象变换法则作出函数的图象，由图象推断各性质。‎ 解：，所以其图象为双曲线 从而，定义域、值域，在上递‎1‎ ‎-2‎ o x y y=-2‎ x=1‎ ‎（1，-2）‎ 减，对称轴、对称中心（1，-2），顶点坐标（0，-3）和（2，-1）。‎ 而且渐近线 ‎ 点评；从新的、深化的角度理解反比例函数。‎ 例2.若函数在上恒为正值，求实数的取值范围。‎ 解析：若把此函数视为关于的二次函数，则问题变得较为复杂，而若把此函数视作关于的函数，则为一次函数，可使之简单化。‎ 解：原函数化为：为关于的一次函数，‎ 所以，只需。‎ 点评：1.充分利用一次函数的恒单调性。2.学会换个角度看问题。‎ ‎2求二次函数的解析式 例3已知二次函数f(x)满足f(2)= -1，，且f(x)的最大值是8，试确定此二次函数。‎ 思维分析：恰当选择二次函数的解析式，且得的对称轴为， 故或f(-1)= -1，故有：‎ 解：‎ 法一：利用一般式 6‎ 设f(x)=ax2+bx+c(a≠0)，由题意得：或解得： ‎ ‎∴f(x)= - 4x2+4x+7‎ 法二：利用顶点式 ‎∵对称轴 又最大值是8‎ ‎∴可设，由f(2)= -1可得a= - 4 ‎ 法三：由已知f(x)+1=0的两根为x1=2,x2=-1，故可设f(x)+1=a(x-2)(x+1)即f(x)=ax2-ax‎-2a-1,又得a= - 4或a=0(舍) ∴f(x)= - 4x2+4x+7‎ 练习（变式1）已知二次函数f(x)=ax2+bx+c满足下列条件：‎ ‎(1)图象过原点 (2)f(-x+2002)=f(x-2000) (3)方程f(x)=x有重根。‎ 解：由(1)得：c=0,由(2)对称轴可确定，‎ 由(3) f(x)=x即ax2+（b-1）x+c=0有重根 例4.‎ ‎      设二次函数f(x)=ax2+bx+c(a>0),方程f(x)-x=0的两个根满足             (Ⅰ)当x∈(0,)时,证明x0,又a>0,得 　　            　F(x)=a(x-)(x-)>0， 即x0,1+a(x-)=1+ax-a>1-a>0 　得   -f(x)>0. 　　         　由此得f(x)< .   　　　 　　                      ‎ ‎          (Ⅱ)依题意知        　　         因为x1,x2是方程f(x)-x=0的根,即是方程a+(b-1)x+c=0的根.   　　                                                     　　. 　　         因为a<1,所以      .    　　　　　　　     ‎ ‎（四）巩固练习：‎ ‎1．函数是单调函数的充要条件是 （ ）‎ ‎ ‎ 分析：对称轴，∵函数是单调函数，∴对称轴在区间 的左边，即，得．‎ ‎2．已知二次函数的对称轴为，截轴上的弦长为，且过点，求函数的解析式．‎ 解：∵二次函数的对称轴为，设所求函数为，又∵截 6‎ 轴上的弦长为，∴过点，又过点，‎ ‎∴， ，‎ ‎∴．‎ ‎3．已知函数的最大值为，求的值 ．‎ 分析：令，问题就转二次函数的区间最值问题．‎ 解：令，，‎ ‎∴，对称轴为，‎ ‎（1）当，即时，，得或（舍去）．‎ ‎（2）当，即时，函数在单调递增，‎ 由，得．‎ ‎（3）当，即时，函数在单调递减，‎ 由，得（舍去）．‎ 综上可得：的值为或．‎ 四、小结：‎ ‎1二次函数f(x)=ax2+bx+c(a≠0)的图象形状、对称轴、开口方向等是处理二次函数问题的重要依据。‎ ‎2．二次函数在闭区间上，必有最大值和最小值，当含有参数时，须对参数分区间讨论。‎ ‎3．二次方程根的分布问题，可借助二次函数图象列不等式组求解。‎ ‎4．三个二次问题（二次函数、二次方程、二次不等式）是中学数学中基础问题，以函数为核心，三者密切相连。‎ 五、作业：‎ 6‎