2018高考立体几何复习最新题型归纳 31页

‎2018高考复习立体几何最新题型总结（文数）‎ 题型一：空间几何体的结构、三视图、旋转体、斜二测法 了解柱、锥、台、球体及其简单组合体的结构特征，并能运用这些特征描述现实生活中的简单物体的结构。能画出简单空间几何体的三视图，能识别上述三视图所表示的立体模型，会用斜二测画法画出它们的直观图。能用平行投影与中心投影两种方法画出简单空间几何体的三视图与直观图。了解空间几何体的不同表示形式。会画某建筑物的视图与直观图。‎ 例1.将正三棱柱截去三个角（如图1所示分别是三边的中点）得到几何体如图2，则该几何体按图2所示方向的侧视图（或称左视图）为（ ）‎ E F D I A H G B C E F D A B C 侧视 图1‎ 图2‎ B E A．‎ B E B．‎ B E C．‎ B E D．‎ 俯视图 例2.由大小相同的正方体木块堆成的几何体的三视图如图所示，则该几何体中正方体木块的个数是 ．‎ ‎ 正视图 左视图 例3.已知一个正四面体的俯视图如图所示，其中四边形ABCD是边长为2的正方形，则该正四面体的内切球的表面积为（　　）A．6πB．54πC．12πD．48π 例4：如图是一个几何体的三视图，根据图中数据，可得该几何体的 表面积为(　 　)‎ A． B．‎ C． D．‎ ‎ 主视图 左视图 俯视图 例5：四棱锥的顶点P在底面ABCD中的投影恰好是A，‎ 其三视图如图，则四棱锥的表面积为( ) ‎ A. B. C. D. 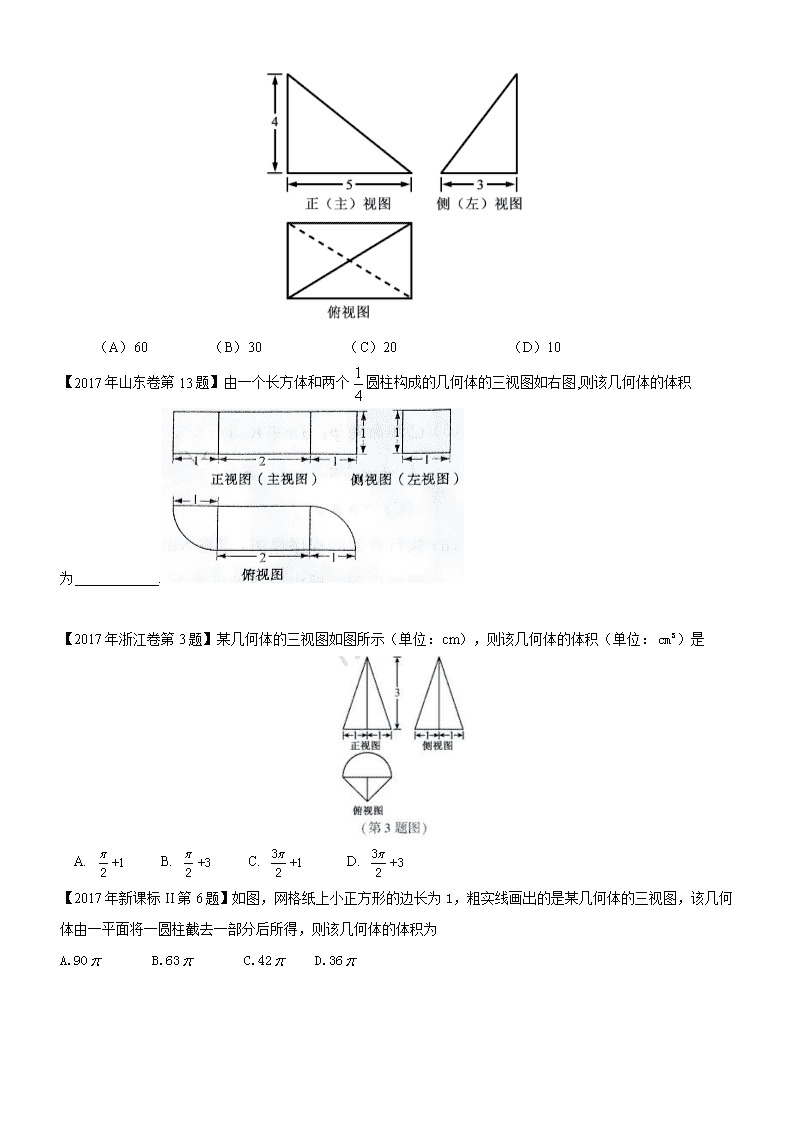‎ 例6：三棱柱ABC—A1B1C1的体积为V，P、Q分别为AA1、CC1上的点，且满足AP=C1Q，则四棱锥B—APQC的体积是___________‎ 例7：如图，斜三棱柱ABC—中，底面是边长为a的正三角形，侧棱长为 b，侧棱AA’与底面相邻两边AB、AC都成450角，求此三棱柱的侧面积和体积．‎ 例8：如图是一个几何体的三视图，根据图中的数据（单位：cm），可知几何体的体积是_________‎ ‎ ‎ ‎2‎ ‎2‎ 主视图 ‎2‎ ‎2‎ 侧视图 ‎2‎ ‎1‎ ‎1‎ 俯视图 真题：‎ ‎【2017年北京卷第6题】某三棱锥的三视图如图所示，则该三棱锥的体积为 ‎（A）60 （B）30 （C）20 （D）10‎ ‎【2017年山东卷第13题】由一个长方体和两个圆柱构成的几何体的三视图如右图,则该几何体的体积为 .‎ ‎【2017年浙江卷第3题】某几何体的三视图如图所示（单位：cm），则该几何体的体积（单位：）是 A. B. C. D. ‎ ‎【2017年新课标II第6题】如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，该几何体由一平面将一圆柱截去一部分后所得，则该几何体的体积为 A.90 B.63 C.42 D.36 ‎ 1、 ‎（2016年山东高考）一个由半球和四棱锥组成的几何体，其三 视图如图所示.则该几何体的体积为 ‎（A） （B） （C） （D）‎ ‎【答案】D ‎3、（2016年天津高考）将一个长方形沿相邻三个面的对角线截去一个棱锥，得到的几何体的正视图与俯视图如图所示，则该几何体的侧（左）视图为（ ）‎ ‎ ‎ ‎ ‎ ‎【答案】B ‎4、（2016年全国I卷高考）如图，某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径.若该几何体的体积是，则它的表面积是 ‎（A）17π （B）18π （C）20π （D）28π ‎ ‎【答案】A ‎6、（2016年全国II卷高考）如图是由圆柱与圆锥组合而成的几何体的三视图，则该几何体的表面积为（ ）‎ ‎（A）20π （B）24π （C）28π （D）32π ‎【答案】C ‎7、（2016年全国III卷高考）如图，网格纸上小正方形的边长为1，粗实现画出的是某多面体的三视图，则该多面体的表面积为 ‎（A） （B） （C）90 （D）81‎ ‎【答案】B ‎1、（2016年北京高考）某四棱柱的三视图如图所示，则该四棱柱的体积为___________.‎ ‎【答案】‎ ‎2、（2016年四川高考）已知某三菱锥的三视图如图所示，则该三菱锥的体积 。‎ ‎【答案】‎ ‎3、（2016年浙江高考）某几何体的三视图如图所示（单位：cm），则该几何体的表面积是______cm2,体积是______cm3.‎ 斜二测法：‎ 例9：一个水平放置的平面图形的斜二测直观图是一个底角为，腰和上底边均为1的等腰梯形，则这个平面图形的面积是（ ）‎ ‎ A． B． C． D． ‎ 例10：对于一个底边在轴上的三角形，采用斜二测画法作出其直观图，其直观图面积是原三角形面积的（ ）‎ A． 倍 B．倍 C．倍 D．倍 例11：如图，已知四边形ABCD的直观图是直角梯形A1B1C1D1，且A1B1＝B1C1＝2A1D1＝2，‎ 则四边形ABCD的面积为(　 　)‎ A．3 B．3 ‎ ‎ C．6 D．6‎ 例12：用斜二测画法画一个水平放置的平面图形为如下图的一个正方形，则原来图形的形状是（　　）‎ 旋转体：‎ 例13：下列几何体是旋转体的是（ ）‎ ‎ A B C D 例14：如图，在四边形中，，，，，，求四边形绕AD旋转一周所成几何体的表面积及体积.‎ 真题：‎ ‎【2015高考山东，文9】已知等腰直角三角形的直角边的长为,将该三角形绕其斜边所在的直线旋转一周而形成的曲面所围成的几何体的体积为( )‎ ‎（A） （B） （）2 （）4 题型二：定义考察类题型 ‎ 例15：已知直线、,平面，则下列命题中假命题是( )‎ A．若，,则 B．若，,则 C．若，,则 D．若，,,,则 例16：给定下列四个命题：‎ ‎①若一条直线与一个平面平行，那么过这条直线的平面与这个面相较，则这线平行于交线 ‎②若一条直线与一个平面垂直，那么这条直线垂直于这个平面内的任一直线 ‎③若两个平面平行，那么分别在这两个平面内的两条直线平行 ‎④若两个平面垂直，那么分别在这两个平面内的两直线垂直 其中，为真命题的是( )‎ ‎ A．和 B．和 C．和 D．和 例17：已知是两条不同直线，是三个不同平面，下列命题中正确的是（ ）‎ A．若，m,则m B． ‎ C． D．‎ 例18：已知是两条不同的直线，是两个不同的平面，有下列命题：‎ ‎ ①若，则； ②若，，则；‎ ‎ ③若，则； ④若，则；‎ ‎ 其中真命题的个数是（ ）‎ ‎ A．1个 B．2个 C．3个 D．4个 例19：如图，四棱锥S—ABCD的底面为正方形，SD底面ABCD，则下列结论中不正确的是（ ）‎ A、AC⊥SB B、AB∥平面SCD C、SA与平面SBD所成的角等于SC与平面SBD所成的角 D、AB与SC所成的角等于DC与SA所成的角 例20：已知为不同的平面，A、B、M、N为不同的点，为直线，下列推理错误的是（　　　）‎ A. B.‎ C. D.且A、B、M不共线重合 ‎ 真题：‎ ‎【2016年浙江高考】已知互相垂直的平面 交于直线l.若直线m，n满足m∥α，n⊥β，则（ ）‎ A.m∥l B.m∥n C.n⊥l D.m⊥n ‎【答案】C ‎【2015高考浙江，文4】设，是两个不同的平面，，是两条不同的直线，且，（ ）‎ A．若，则 B．若，则 C．若，则 D．若，则 ‎【2015高考广东，文6】若直线和是异面直线，在平面内，在平面内，是平面与平面的交线，则下列命题正确的是（ ）‎ A．至少与，中的一条相交 B．与，都相交 C．至多与，中的一条相交 D．与，都不相交 ‎【2015高考湖北，文5】表示空间中的两条直线，若p：是异面直线；q：不相交，则（ ）‎ A．p是q的充分条件，但不是q的必要条件 ‎ B．p是q的必要条件，但不是q的充分条件 C．p是q的充分必要条件 ‎ D．p既不是q的充分条件，也不是q的必要条件 题型三：直线与平面、平面与平面平行的判定与性质 证明平行的方法：‎ 线线平行：相似，全等；平行线判断定理（内错角相等，同旁内角互补等），（高中阶段一般不考，只作为转化的一个桥梁）。‎ 线面平行：（1）根据定理证明（）；（2）通过面面平行的性质定理（）‎ F A B C P D E 面面平行：（1）平面中分别有两条相交线与平面的两条相交线平行 （2）平面的法向量与平面的法向量平行 例21：如图，在四棱锥中，底面是边长为的正方形，‎ 侧面，且，若、分别 为、的中点.‎ ‎（1）求证：∥平面；‎ ‎（2）求证：平面 平面.‎ 例22：如图所示，在正方体ABCD-A1B1C1D1中，M，N分别是C1C，B1C1的中点，求证：MN平面A1BD.‎ B C A A1‎ B1‎ C1‎ D E 例23：如图，直棱柱中，D，E分别是AB，的中点，=AC=CB=AB。‎ ‎（Ⅰ）证明：//‎ ‎（Ⅱ）求A到面ACD的距离 例24：如图所示，在四棱锥O-ABCD中，底面ABCD四边长为1的菱形，‎ ‎∠ABC=, OA⊥底面ABCD,OA=2,M为OA的中点，N为BC的中点 ‎（Ⅰ）证明：直线MN∥平面OCD；‎ ‎（Ⅱ）求异面直线AB与MD所成角的大小； ‎ ‎（Ⅲ）求点B到平面OCD的距离。‎ 例25：如图，已知矩形和矩形所在平面互相垂直，点，分别在对角线，上，且，．求证：平面．‎ 例26：如图，在正方体ABCD—A1B1C1D1中，M、N、P分别是C1C、B1C1、C1D1的中点，求证：平面MNP∥平面A1BD.‎ 例27：已知四棱锥P-ABCD中, 底面ABCD为平行四边形. 点M、N、Q分别在PA、BD、PD上, 且PM：MA=BN：ND=PQ：QD. 求证：平面MNQ∥平面PBC. ‎ N M P D C Q B A 题型四：线与面、面与面的垂直的证明方法 三垂线定理：如果在平面内的一条直线与平面的一条斜线在这个平面内的射影垂直，则它也和这条直线垂直。‎ 三垂线逆定理：如果：如果在平面内的一条直线与平面的一条斜线垂直，则它也和这条直线在这个平面内的射影垂直。‎ 例28：直三棱柱ABC-A1B1C1中，，E是A1C的中点，且交AC于D， ．‎ D E A1‎ C B A C1‎ B1‎ ‎（I）证明：平面；（II）证明：平面．‎ 例29：如图所示，已知四棱锥的底面是菱形；‎ 平面,‎ ‎，点为的中点．‎ ‎（Ⅰ）求证：平面；‎ ‎（Ⅱ）求证面．‎ 例30：如图，在棱长为的正方体中，分别 F G E D C A B A1‎ B1‎ D1‎ C1‎ ‎·‎ ‎·‎ 是 的中点。‎ ‎（1）求证：平面平面；‎ ‎（2）求证：平面 例31：如图，在三棱柱中，侧面，均为正方形，∠,点是棱的中点.‎ A B C C1‎ B1‎ A1‎ D ‎（Ⅰ）求证：⊥平面；‎ ‎（Ⅱ）求证：平面；‎ 例32：如图所示，四棱锥P—ABCD中，ABAD，CDAD，PA底面ABCD，PA=AD=CD=2AB=2，‎ M为PC的中点。‎ ‎(1)求证：BM∥平面PAD； (2)在侧面PAD内找一点N，使MN平面PBD；‎ ‎(3)求直线PC与平面PBD所成角的正弦。‎ 例33：在如图所示的几何体中，四边形是正方形，,,分别为、的中点，且．‎ ‎ （Ⅰ）求证：平面;‎ ‎ （Ⅱ）求三棱锥．‎ 例34：如图，在直三棱柱ABC—A1B1C1中，AC=BC，点D是AB的中点。‎ ‎（1）求证：‎ ‎（2）求证：平面⊥平面 例35：如图所示，已知矩形ABCD中，AB=10，BC=6，将矩形沿对角线BD把△ABD折起，使A移到点，且在平面BCD上的射影O恰好在CD上．‎ ‎（Ⅰ）求证：；‎ ‎（Ⅱ）求证：平面平面；‎ ‎（Ⅲ）求三棱锥的体积． ‎ 真题：‎ ‎【2016年上海高考】如图，在正方体ABCD−A1B1C1D1中，E、F分别为BC、BB1的中点，则下列直线中与直线EF相交的是（ ）‎ ‎(A)直线AA1 (B)直线A1B1 (C)直线A1D1 (D)直线B1C1‎ ‎【2017年新课标I卷第6题】如图，在下列四个正方体中，A，B为正方体的两个顶点，M，N，Q为所在棱的中点，则在这四个正方体中，直接AB与平面MNQ不平行的是（ ）‎ ‎【2017年新课标III卷第10题】在正方体中，E为棱CD的中点，则 A． B． C． D．‎ ‎【2015高考山东，文18】 如图，三棱台中，分别为的中点.‎ ‎（I）求证：平面；‎ ‎（II）若求证：平面平面. ‎ 题型五：空间中的夹角 知识点：夹角的分类：线线夹角、线面夹角、面面夹角 三者在计算或证明时的转换关系：‎ 面面 线面 线线 计算三种夹角的方法：勾股定理、向量、坐标等，对于夹角问题我们一般分为三个步骤：‎ ‎①找角，②证明所找的角，‎ ‎③计算所找角的大小（切记不可找出来之后不证明就开始计算）‎ 异面直线的夹角问题：‎ 例36：在四棱锥P—ABCD中，底面ABCD是一直角梯形，与底面成30°‎ ‎（1）若为垂足，求证：；‎ ‎（2）在（1）的条件下，求异面直线AE与CD所成角的正切值；‎ 例37：如图，已知P是平行四边形ABCD所在平面外一点，M、N分别是AB、PC的中点 ‎（1）求证：MN//平面PAD；（2）若，，求异面直线PA与MN所成的角的大小 例38：如图，四边形ABCD是边长为1的正方形，，‎ ‎，且MD=NB=1，E为BC的中点，求异面直线 NE与AM所成角的余弦值 例39：如图，在正方体中，、分别是、的中点，则异面直线与所成的角的大小是____________。‎ 例40：已知正四面体中，各边长均为，如图所示，分别为的中点，连接，求异面直线所成角的余弦值。‎ 例41：已知S是正三角形ABC所在平面外的一点，如图SA＝SB＝SC，且ASB＝BSC＝CSA＝，M、N分别是AB和SC的中点．求异面直线SM与BN所成的角的余弦值．‎ B M A N C S 例42：已知三棱柱的侧棱与底面边长都相等，在底面上的射影为的中点，则异面直线与所成的角的余弦值为（ ）‎ ‎（A） （B） （C） (D) w.w.w.k.s.5.u.c.o.m ‎ 例43：如图,在正方体中，分别是的中点。‎ ‎（1）若为的中点，证明：平面∥平面 ‎ ‎（2）求异面直线与所成的角[来源:Z+xx+k.Com]‎ 例44：如图，四面体ABCD中，AB⊥BC，AB⊥BD，BC⊥CD，且AB＝BC＝6，BD＝8，E是AD中点，求BE与CD所成角的余弦值。‎  ‎ 线面夹角（了解）：‎ 例45：如图，四棱锥P-ABCD中，底面ABCD为菱形，PA⊥底面ABCD，AC=2，PA=AD=2，E是PC上的一点，‎ ‎ 设二面角A-PB-C为90°，求PD与平面PBC所成角的大小。 ‎ 例46：如图，直三棱柱中，,D、E分别是，的中点,平面.‎ ‎（1）证明：AB=AC ‎（2）设二面角A-BD-C为，求与平面BCD所成的角的大小 ‎ ‎ 真题：‎ ‎【2016年全国I卷高考】如平面过正方体ABCD—A1B1C1D1的顶点A，,，，则m，n所成角的正弦值为 ‎（A）（B）（C）（D）‎ ‎【2015高考浙江，文18】如图，在三棱锥中，在底 面ABC的射影为BC的中点，D为的中点.‎ ‎（1）证明：； （2）求直线和平面所成的角的正弦值.‎ ‎【2014高考，文18】如图，四棱锥中，底面为菱形，底面，，，是上的一点，。‎ ‎（Ⅰ）证明：平面；‎ ‎（Ⅱ）设二面角为，求与平面所成角的大小。‎ ‎【2015高考湖南，文18】（本小题满分12分）如图4，直三棱柱的底面是边长为2的正三角形，分别是的中点。（I）证明：平面平面；‎ ‎（II）若直线与平面所成的角为，求三棱锥的体积。‎ 题型六：距离问题：点线距离（定义法、等体积法、向量法、空间坐标法）；线面距离；面面距离。‎ 例47：已知正四棱柱的地面边长为1，则棱场为2，点E为的中点，求点到平面BDE的距离。‎ 例48：已知正四棱柱中 ，，，为的中点，则直线与平面的距离为（ ）‎ ‎ A. B. C. D.‎ 例49：在中,AB=15，，若所在平面外一点P到A、B、C的距离都是14，则P到的距离是（ ）‎ ‎ A.13 B.11 C.9 D.7‎ 例50：如图，在四棱锥中，底面四边长为1的菱形，, , ,为的中点，为的中点 ‎（Ⅰ）证明：直线； ‎ ‎（Ⅱ）求异面直线AB与MD所成角的大小； ‎ ‎（Ⅲ）求点B到平面OCD的距离。‎ 例51：为平面，AB=5,A,B在棱l上的射影分别为A′，B′，AA′＝3，BB′＝2.若二面角的大小为，求，点B到平面的距离为_____________ ‎ 例52：P为矩形ABCD所在平面外一点，且PA⊥平面ABCD，P到B，C，D三点的距离分别是，，，则P到A点的距离是（　 ）‎ ‎ A.1 B.2 C. D.4‎ 例53：如图，在四棱锥中，底面四边长为1的菱形，, , ,为的中点，为的中点 ‎（Ⅰ）证明：直线；‎ ‎（Ⅱ）求异面直线AB与MD所成角的大小；（Ⅲ）求点B到平面OCD的距离 例54：如图,直四棱柱ABCD – A1B1C1D1中,AB//CD,AD⊥AB,AB=2,AD=,AA1=3,E为CD上一点,DE=1,EC=3‎ ‎(1) 证明:BE⊥平面BB1C1C;‎ ‎(2) 求点B1 到平面EA1C1 的距离 例55：如图，已知多面体ABC－DEFG中，AB、AC、AD两两互相垂直，平面ABC∥平面DEFG，平面BEF∥平面ADGC，AB=AD=DG=2，AC=EF=1。‎ ‎（1）试判断CF是否与平面ABED平行？并说明理由；‎ ‎（2）求多面体ABC－DEFG的体积。‎ 例56：如图，四面体ABCD中，O、E分别是BD、BC的中点，‎ ‎（I）求证：平面BCD；‎ ‎（II）求点E到平面ACD的距离。‎ 例57：如图，在四棱锥P-ABCD中，PD⊥平面ABCD，PD=DC=BC=1，AB=2，AB∥DC，∠BCD=900。‎ (1) 求证：PC⊥BC；‎ (2) 求点A到平面PBC的距离。‎ 题型七：求体积问题 例58：如图，为多面体，平面与平面垂直，点在线段上，，，△OAB，△OAC，△ODE，△ODF都是正三角形。‎ ‎（Ⅰ）证明直线；（Ⅱ）求棱锥的体积.‎ 例59：如图，三棱柱ABC－A1B1C1中，侧棱垂直底面，∠ACB=90°，AC=BC=AA1，D是棱AA1的中点 ‎(Ｉ)证明：平面BDC1⊥平面BDC ‎（Ⅱ）平面BDC1分此棱柱为两部分，求这两部分体积的比.‎ C B A D C1‎ A1‎ 真题：‎ ‎【2017年新课标I卷第18题】如图，在四棱锥P-ABCD中，AB//CD，且 ‎（1）证明：平面PAB⊥平面PAD；‎ ‎（2）若PA=PD=AB=DC,,且四棱锥P-ABCD的体积为，求该四棱锥的侧面积.‎ ‎【2017年新课标II第18题】如图，四棱锥P-ABCD中，侧面PAD为等边三角形且垂直于底面ABCD，AB=BC=AD, ∠BAD=∠ABC=90°。‎ （1） 证明：直线BC∥平面PAD;‎ （2） 若△PAD面积为2，求四棱锥P-ABCD的体积。‎ ‎ ‎ ‎【2017年新课标III卷第19题】如图，四面体ABCD中，△ABC是正三角形，AD=CD．‎ ‎（1）证明：AC⊥BD；‎ ‎（2）已知△ACD是直角三角形，AB=BD．若E为棱BD上与D不重合的点，且AE⊥EC，求四面体ABCE与四面体ACDE的体积比．‎ ‎【2016年全国I卷高考】如图，已知正三棱锥P-ABC的侧面是直角三角形，PA=6，顶点P在平面ABC内的正投影为点D，D在平面PAB内的正投影为点E，连结PE并延长交AB于点G.‎ ‎（I）证明：G是AB的中点；‎ ‎（II）在图中作出点E在平面PAC内的正投影F（说明作法及理由），并求四面体PDEF的体积．‎ ‎【2016年全国II卷高考】如图，菱形的对角线与交于点，点、分别在，上，，‎ 交于点，将沿折到的位置.‎ ‎（Ⅰ）证明：；‎ ‎（Ⅱ）若,求五棱锥体积.‎ ‎【2016年全国III卷高考】如图，四棱锥中，平面，，，，为线段上一点，，为的中点．‎ ‎（I）证明平面；‎ ‎（II）求四面体的体积.‎ ‎【2015高考新课标1，文18】（本小题满分12分）如图四边形ABCD为菱形，G为AC与BD交点，，‎ ‎（I）证明：平面平面；‎ ‎（II）若， 三棱锥 的体积为，求该三棱锥的侧面积.‎ ‎【2015高考北京，文18】（本小题满分14分）如图，在三棱锥中，平面平面，为等边三角形，‎ 且，，分别为，的中点．‎ ‎（I）求证：平面；（II）求证：平面平面；（III）求三棱锥的体积．‎ ‎【2015高考重庆，文20】如题（20）图，三棱锥P-ABC中，平面PAC平面ABC，ABC=，点D、E在线段AC上，且AD=DE=EC=2，PD=PC=4，点F在线段AB上，且EF//BC.‎ ‎(Ⅰ)证明：AB平面PFE. (Ⅱ)若四棱锥P-DFBC的体积为7，求线段BC的长.‎ 题型八：翻折与展开问题及探索问题 例60：如图所示，等腰的底边，高，点是线段上异于点的动点，点在边上，且，现沿将折起到的位置，使，记，表示四棱锥的体积．‎ P E D F B C A ‎（1）求的表达式；（2）当为何值时，取得最大值？‎ ‎（3）当取得最大值时，求异面直线与所成角的余弦值．‎ 例61：在直角梯形中（图中数字表示线段的长度），将直角梯形沿折起，使平面平面，连结部分线段后围成一个空间几何体， ‎ ‎（Ⅰ）求证：平面；‎ ‎（Ⅱ）求三棱锥的体积．‎ 例62：正方形ABCD的边长为1，分别取边BC、CD的中点E、F，连接AE、EF、AF.以AE、EF、FA为折痕，折叠这个正方形，使点B、C、D重合于一点P，得到一个四面体，如图(2)所示．‎ ‎(1)求证：AP⊥EF；‎ ‎(2)求证：平面APE⊥平面APF.‎ 例63：如图4,在边长为1的等边三角形中,分别是边上的点,,是的中点,与交于点,将沿折起,得到如图5所示的三棱锥,其中.‎ ‎(1) 证明://平面; (2) 证明:平面;‎ ‎(3) 当时,求三棱锥的体积.‎ ‎ ‎ 例68：如图甲，在直角梯形中，，，，是的中点. 现 沿把平面折起，使得（如图乙所示），、分别为、边的中点.‎ ‎（1）求证：平面；‎ 图甲 图乙 ‎（2）求证：平面平面；‎ ‎（3）试探究在上是否存在一点，使得平面,‎ 并说明理由. ‎ 真题：‎ ‎【2015高考陕西，文18】如图1，在直角梯形中，，是的中点，是与的交点，将沿折起到图2中的位置，得到四棱锥.‎ ‎(I)证明：平面；‎ ‎(II)当平面平面时，四棱锥的体积为，求的值.‎ ‎【2014高考，文19】如图所示：边长为2的正方形ABFC和高为2的直角梯形ADEF所在的平面互相垂直且DE=，ED//AF且∠DAF=90°。‎ （1） 求BD和面BEF所成的角的余弦；（2）线段EF上是否 存在点P使过P、A、C三点的平面和直线DB垂直，若存在，‎ 求EP与PF的比值；若不存在，说明理由。‎ ‎【2015高考安徽，文19】如图，三棱锥P-ABC中，PA平面ABC，.‎ ‎（Ⅰ）求三棱锥P-ABC的体积；‎ ‎（Ⅱ）证明：在线段PC上存在点M，使得ACBM，并求的值.‎ ‎【2015高考福建，文20】如图，是圆的直径，点是圆上异于的点，垂直于圆所在的平面，且．‎ ‎（Ⅰ）若为线段的中点，求证平面；（Ⅱ）求三棱锥体积的最大值；‎ ‎（Ⅲ）若，点在线段上，求的最小值．‎ 题型九：球类问题专项练习 一：外接球的有关问题 棱锥的内切、外接球问题 例69：正四面体的外接球和内切球的半径是多少？ ‎ 例70：设棱锥的底面是正方形，且，，‎ 如果的面积为1，试求能够放入这个棱锥的最大球的半径.‎ 例71：一个长方体的各顶点均在同一球面上，且一个顶点上的三条棱长分别为1,2,3，则此球的表面积为______‎ 例72：已知各顶点都在一个球面上的正四棱柱高为4，体积为16，则这个球的表面积为（ ）‎ A. B. C. D. ‎ 例73：一个六棱柱的底面是正六边形，其侧棱垂直于底面，已知该六棱柱的顶点都在同一个球面上，且该六棱柱的体积为，底面周长为3，则这个球的体积为__________‎ 例74：正四棱锥的底面边长和各侧棱长都为，点都在同一球面上，则此球的体积为_______________.‎ 例75：表面积为 的正八面体的各个顶点都在同一个球面上，则此球的体积为 ‎ A． B． C． D．‎ 二：球类的截面问题 例76：球面上有三点、、组成这个球的一个截面的内接三角形三个顶点，其中，、，球心到这个截面的距离为球半径的一半，求球的表面积．‎ 例77：过球表面上一点引三条长度相等的弦、、，且两两夹角都为，若球半径为，求弦的长度．‎ 例78：已知球的面上四点A、B、C、D，，，，则球的体积等于_______________.‎ 例79：已知点A、B、C、D在同一个球面上，，，若，则球的体积是_______________.‎ 例80：球面上有3个点，其中任意两点的球面距离都等于大圆周长的，经过3个点的小圆的周长为，求这个球的半径．‎ 例81：一个正三棱锥的四个顶点都在半径为1的球面上，其中底面的三个顶点在该球的一个大圆上，则该正三棱锥的体积是（ ）‎ A． B． C． D． ‎ 例82：直三棱柱的各顶点都在同一球面上，若,，则此球的表面积等于 ‎ 例83：正三棱柱内接于半径为的球，若两点的球面距离为，则正三棱柱的体积为 　‎ 例84：用两个平行平面去截半径为的球面，两个截面圆的半径为，．两截面间的距离为，求球的表面积．‎ 三：球面距离 例85： 过球面上两点作球的大圆，可能的个数是（　　）．‎ A．有且只有一个　 B．一个或无穷多个 C．无数个　　　　 D．以上均不正确 例86：已知、是半径为的球的球面上两点，它们的球面距离为，求过、的平面中，与球心的最大距离是多少？‎ 例87：在球心同侧有相距的两个平行截面，它们的面积分别为和．求球的表面积．‎ 例88：如图球O的半径为2，圆是一小圆，，A、B是圆上两点，若A，B两点间的球面距离为，则= ‎ 例89：在半径为3的球面上有三点，，球心到平面的距离是，则两点的球面距离是（ ）‎ A. B. C. D. ‎ 四：其它问题 例90：在矩形中，，沿将矩形折成一个直二面角，则四面体的外接球的体积为（ ）‎ A. B. C. D.‎ 例91：一个倒圆锥形容器，它的轴截面是正三角形，在容器内注入水，并放入一个半径为的铁球，这时水面恰好和球面相切．问将球从圆锥内取出后，圆锥内水平面的高是多少？‎ 例92：一个六棱柱的底面是正六边形，其侧棱垂直底面．已知该六棱柱的顶点都在同一个球面上，且该六棱柱的体积为，底面周长为3，则这个球的体积为　　　　　　．‎ 例93：（2012新课标理）已知三棱锥的所有顶点都在球的求面上,是边长为的正三角形,为球的直径,且;则此棱锥的体积为（　 　）‎ A． B． C． D．‎ 例94：（2012辽宁文）已知点P,A,B,C,D是球O表面上的点,PA⊥平面ABCD,四边形ABCD是边长为2正方形.若PA=,则△OAB的面积为______________.‎ 例95：在底面边长为2的正方体容器中，放入大球，再放入一个小球，正好可以盖住盖子（小球与大球都与盖子相切）， 求小球的半径。‎ 例96：自半径为的球面上一点，引球的三条两两垂直的弦，求的值．‎ 例97：在棱长为1的正方体内有两个球相外切且又分别与正方体内切．（1）求两球半径之和；（2）球的半径为多少时，两球体积之和最小．‎ 例98：有一个水平放置的透明无盖的正方体容器,容器高8cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6cm,如果不计容器的厚度,则球的体积为______________. ‎ 真题：‎ ‎【2017年新课标I卷第16题】已知三棱锥S-ABC的所有顶点都在球O的球面上，SC是球O的直径.若平面SCA⊥平面SCB，SA=AC，SB=BC，三棱锥S-ABC的体积为9，则球O的表面积为________.‎ ‎【2017年新课标III卷第9题】已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为 A． B． C． D．‎ ‎【2017年新课标II第15题】长方体的长、宽、高分别为3,2,1，其顶点都在球O的球面上，则球O的表面积为 ‎ ‎【2017年新课标III卷第10题】在正方体中，E为棱CD的中点，则 A． B． C． D．‎ ‎【2017年天津卷第11题】已知一个正方体的所有顶点在一个球面上，若这个正方体的表面积为18，则这个球的体积为 .‎ ‎【2017年江苏卷第6题】如图，在圆柱O1 O2 内有一个球O，该球与圆柱的上、下底面及母线均相切。记圆柱 O1 O2 的体积为V1 ,球O的体积为V2 ，则 的值是 ‎ ‎ ‎