山东春季高考数学试题及详解答案解析 11页

山东省 2015 年普通高校招生（春季）考试 数学试题 注意事项: １.本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分．满分 120 分，考试时间 120 分钟．考试结束后，将本试卷和答题卡一并交 回． ２.本次考试允许使用函数型计算器，凡使用计算器的题目，最后结 果精确到 0.01． 第Ⅰ卷（选择题，共 60 分） 一、选择题（本大题 20 个小题，每小题 3 分，共 60 分．在每小题列出的四个选 项中，只有一项符合题目要求，请将符合题目要求的选项字母选出，填涂在答题 卡上） 1．若集合 A＝{1，2，3}，B＝{1，3}，则 A ∩B 等于（ ） （A）{1，2，3} （B）{1，3} （C） {1，2} （D）{2} 2．|x－1|＜5 的解集是（ ） （A）(－6，4) （B）（－4，6） （C） (－∞, －6)∪(4, ＋∞) （D）(－∞, －4 )∪（6，＋∞) 3．函数 y＝ x + 1+ 1 x的定义域为（ ） （A）{x| x≥－1 且 x≠0} （B）{x|x≥－1} （C）{x x＞－1 且 x≠0} （D）{x|x＞－1} 4.“圆心到直线的距离等于圆的半径”是“直线与圆相切”的 （A）充分不必要条件 （B）必要不充分条件 （C）充要条件 （D）既不充分也不必要条件 5．在等比数列{an}中，a2＝1，a4＝3，则 a6 等于（ ） （A）-5 （B）5 （C）-9 （D）9 6.如图所示，M 是线段 OB 的中点，设向量→OA ＝→a ，→OB ＝→b ，则→AM 可以表示为（ ） （A）→a + 1 2→b （B） －→a + 1 2→b （C）→a － 1 2→b （D）－→a － 1 2→b 7．终边在 y 轴的正半轴上的角的集合是（ ） （A）{x|x＝π 2＋2kπ，k∈Z } （B）{x|x＝π 2＋kπ} （C）{x|x＝－π 2＋2kπ，k∈Z } （D）{x|x＝－π 2＋kπ，k∈Z } 8．关于函数 y＝－x2+2x，下列叙述错误的是（ ） （A）函数的最大值是 1 （B）函数图象的对称轴是直线 x=1 （C）函数的单调递减区间是[－1，＋∞) （D）函数图象过点（2，0） 9．某值日小组共有 5 名同学，若任意安排 3 名同学负责教室内的地面卫生，其余 2 名同学 负责教室外的走廊卫生，则不同的安排方法种数是（ ） （A）10 （B）20 （C）60 （D）100 10．如图所示，直线 l 的方程是（ ） （A） 3x－y－ 3＝0 （B） 3x－2y－ 3＝0 （C） 3x－3y－1＝0 （D）x－ 3y－1＝0 11．对于命题 p，q，若 p∧q 为假命题”，且 p∨q 为真命题，则（ ） （A）p，q 都是真命题 （B）p，q 都是假命题 （C）p，q 一个是真命题一个是假命题 （D）无法判断 12．已知函数 f (x)是奇函数，当 x＞0 时，f (x)＝x2＋2，则 f (－1)的值是（ ） （A）－3 （B）－1 （C）1 （D）3 13．已知点 P（m，－2）在函数 y＝log 1 3 x 的图象上，点 A 的坐标是（4，3），则︱→AP ︱的值是 （ ） （A） 10 （B）2 10 （C）6 2 （D）5 2 14．关于 x,y 的方程 x2+m y2＝1，给出下列命题： B O M A ①当 m＜0 时，方程表示双曲线；②当 m＝0 时，方程表示抛物线；③当 0＜m＜1 时，方程表 示椭圆；④当 m＝1 时，方程表示等轴双曲线；⑤当 m＞1 时，方程表示椭圆。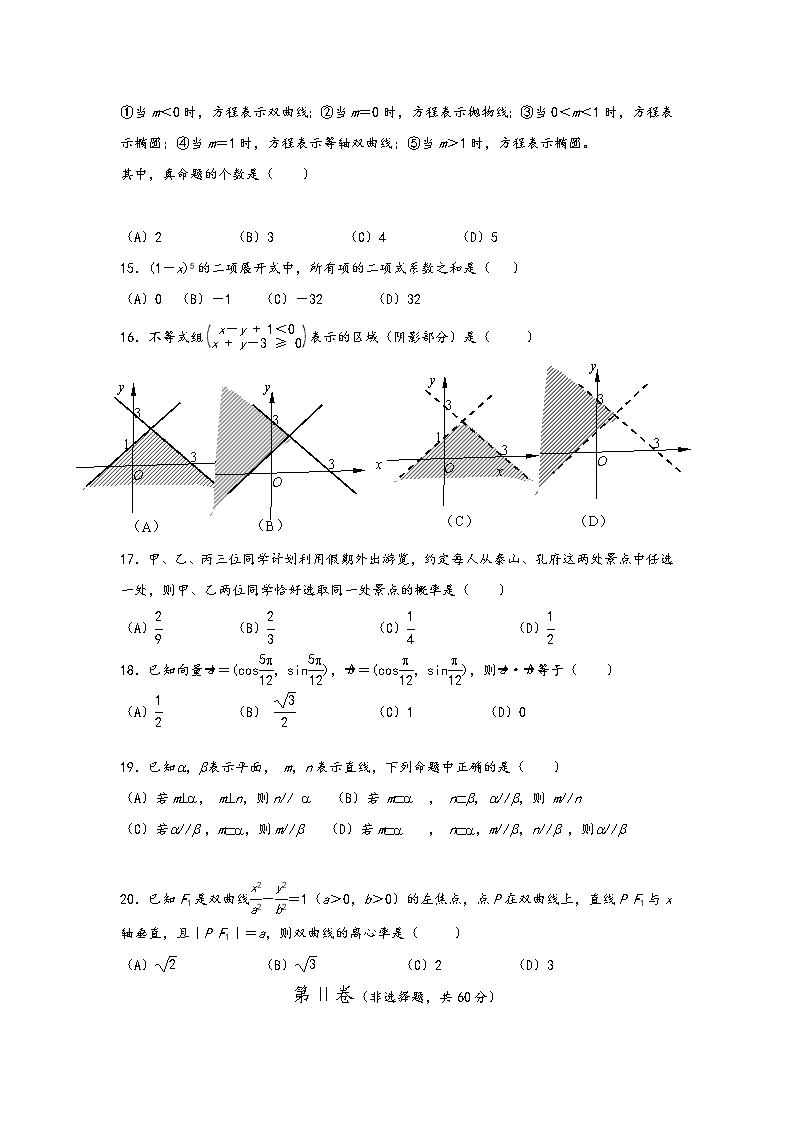 其中，真命题的个数是（ ） （A）2 （B）3 （C）4 （D）5 15．(1－x)5 的二项展开式中，所有项的二项式系数之和是（ ） （A）0 （B）－1 （C）－32 （D）32 16．不等式组( x－y + 1＜0 x + y－3 ≥ 0)表示的区域（阴影部分）是（ ） 17．甲、乙、丙三位同学计划利用假期外出游览，约定每人从泰山、孔府这两处景点中任选 一处，则甲、乙两位同学恰好选取同一处景点的概率是（ ） （A） 2 9 （B） 2 3 （C） 1 4 （D） 1 2 18．已知向量→a ＝(cos 5π 12，sin 5π 12)，→b ＝(cos π 12，sin π 12)，则→a ·→b 等于（ ） （A） 1 2 （B） 3 2 （C）1 （D）0 19．已知α，β表示平面， m，n 表示直线，下列命题中正确的是（ ） （A）若 m⊥α， m⊥n，则 n// α （B）若 m⊂α ， n⊂β, α//β，则 m//n （C）若α//β ，m⊂α，则 m//β （D）若 m⊂α ， n⊂α，m//β，n//β ，则α//β 20．已知 F1 是双曲线 x2 a2－ y2 b2＝1（a＞0，b＞0）的左焦点，点 P 在双曲线上，直线 P F1 与 x 轴垂直，且︱P F1︱＝a，则双曲线的离心率是（ ） （A） 2 （B） 3 （C）2 （D）3 第Ⅱ卷（非选择题，共 60 分） （A） （B） （C） （D） x 1 y O 3 31 y O 3 3 x 1 y O 3 3 x 1 y O 3 3 二、填空题（本大题共 5 个题，每小题 4 分，共 20 分，请将答案填在答题卡上 相应题号的横线上） 21.直棱柱的底面是边长为 a 的菱形，侧棱长为 h，则直棱柱的侧面积是________． 22．在△ABC 中，∠A＝105°，∠C＝45°，AB＝2 2， BC 等于________． 23．计划从 500 名学生中抽取 50 名进行问卷调查，拟采用系统抽样方法，为此将他们逐一 编号为 1～500，并对编号进行分段，若从第一个号码段中随机抽出的号码是 2，则从第五个 号码段中抽出的号码应是________． 24．已知椭圆的中心在坐标原点，右焦点与圆 x2+m y2－6 m－7＝0 的圆心重合，长轴长等 于圆的直径，则短轴长等于________． 25．集合 M，N，S 都 是非空集合，现规定如下运算： M⊙N⊙S＝{x|x∈(M∩N)∪(N∩S)∪(S∩M)，且 x∉ M∩N∩S }． 若集合 A＝{x|a＜x＜b}，B＝{x|c＜x＜d} ，C＝{x|e＜x＜f}，其中实数 a，b，c，d，e，f 满足： （1）ab＜0，cd＜0；ef＜0；（2）b－a＝d－c＝f－e；（3）b＋a＜d＋c＜f＋e． 计算 A⊙B⊙C＝_____________________________________． 三、解答题（本大题共 5 个小题，共 40 分，请在答题卡相应的题号处写出解答过程） 26．（本小题 6 分）某学校合唱团参加演出，需要把 120 名演员排成 5 排，并且从第二排起， 每排比前一排多 3 名 ，求第一排应安排多少名演员。 27. （本小题 8 分）已知函数 y ＝2sin(2x+φ)，x∈R, 0＜φ＜π 2，函数的部分图象如图所 xO y 1 示，求 （1）函数的最小正周期 T 及 φ 的值； （2）函数的单调递增区间。 28．（本小题 8 分）已知函数 f (x)＝a x （a＞0 且 a≠1）在区间[－2，4]上的最大值是 16， （1）求实数 a 的值； （2）若函数 g (x)＝log2(x2－3x＋2a)的定义域是 R，求满足不等式 log2(1－2t)≤1 的实数 t 的取值范围． 29．（本小题 9 分）如图所示，在四棱锥 S－ABCD 中，底面 ABCD 是正方形，平面 SAD⊥平面 ABCD，SA＝SD＝2，AB＝3. （1）求 SA 与 BC 所成角的余弦值； （2）求证：AB⊥SD． 30．（本小题 9 分）已知抛物线的顶点是坐标原点 O，焦点 F 在 x 轴的正半轴上，Q 是抛物线 上的点，点 Q 到焦点 F 的距离为 1，且到 y 轴的距离是 3 8 （1）求抛物线的标准方程； （2）若直线 l 经过点 M（3，1），与抛物线相交于 A，B 两点，且 OA⊥OB，求直线 l 的方 程． 答案 BA A CD S S S S 1.【考查内容】集合的交集 【答案】B 2.【考查内容】绝对值不等式的解法 【答案】B 【解析】 . 3.【考查内容】函数的定义域 【答案】A 【解析】 且 得该函数的定义域是 . 4.【考查内容】充分、必要条件 【答案】C 【解析】“圆心到直线的距离等于圆的半径” “直线与圆相切”，“直线与圆相切” “圆心到直线的距离等于圆的半径”. 5.【考查内容】等比数列的性质 【答案】D 【解析】 ， . 6. 【考查内容】向量的线性运算 【答案】B 【解析】 . 7.【考查内容】终边相同的角的集合 【答案】A 【解析】终边在 y 轴正半轴上的角的集合是 8.【考查内容】二次函数的图象和性质 【答案】C 【解析】 ，最大值是 1，对称轴是直线 ，单调递减区间是 ，（2,0）在函数图象上. 9.【考查内容】组合数的应用 【答案】A 【解析】从 5 人中选取 3 人负责教室内的地面卫生，共有 种安排方法.（选取 3 人后 剩下 2 名同学干的活就定了） 10【考查内容】直线的倾斜角，直线的点斜式方程 【答案】D 【解析】由图可得直线的倾斜角为 30°，斜率 ，直线 l 与 x 轴的交点为 （1,0），由直线的点斜式方程可得 l： ，即 . 11. 【考查内容】逻辑联结词 1 5 5 1 5 4 6x x x− < ⇒ − < − < ⇒ − < < 1 0x +  0x ≠ { }1 0x x x− ≠且 ⇒ ⇒ 2 4 2 3aq a = = 2 6 4 9a a q= = 1 2AM OM OA b a= − = −     2 ,2x k k  π + π ∈   Z 2 22 ( 1) 1y x x x= − + = − − + 1x = [1, )+∞ 3 5C 10= 3tan30 3k = = 30 ( 1)3y x− = − 3 1 0x y− − = 【答案】C 【解析】由 是假命题可知 p,q 至少有一个假命题，由 是真命题可知 p,q 至少有一 个真命题，∴p,q 一个是真命题一个是假命题 12.【考查内容】奇函数的性质 【答案】A 【解析】 13.【考查内容】对数的运算，向量的坐标运算，向量的模 【答案】D 【解析】∵点 在函数 的图象上，∴ ，∴P 点坐标为 ， . 14.【考查内容】椭圆、双曲线和抛物线的标准方程，等轴双曲线的概念 【答案】B 【解析】当 时，方程表示双曲线；当 时，方程表示两条垂直于 x 轴的直线；当 时，方程表示焦点在 y 轴上的椭圆；当 时，方程表示圆；当 时，方程表 示焦点在 x 轴上的椭圆.①③⑤正确. 15.【考查内容】二项式定理 【答案】D 【解析】所有项的二项式系数之和为 16【考查内容】不等式组表示的区域 【答案】C 【解析】可以用特殊点（0,0）进行验证： ， ，非严格不等式的边界 用虚线表示，∴该不等式组表示的区域如 C 选项中所示. 17.【考查内容】古典概率 【答案】D 【解析】甲、乙两位同学选取景点的不同种数为 ，其中甲、乙两位同学恰好选取同 一处景点的种数为 2，故所求概率为 18.【考查内容】余弦函数的两角差公式，向量的内积的坐标运算 【答案】A 【解析】 19.【考查内容】空间直线、平面的位置关系 【答案】C 【解析】A. 若 ， ，则 或n 在 内；B. 若 ， ， ，则 或 m 与 n 异面；D. 若 ， ， ， ，且 m、n 相交才能判定 ；根据 两平面平行的性质可知 C 正确. 20.【考查内容】双曲线的简单几何性质 p q∧ p q∨ 2( 1) (1) (1 2) 3f f− = − = − + = − ( , 2)P m − 1 3 logy x= 2 1 3 1log 2, ( ) 93m m −= − = = (9, 2)− (5, 5), 5 2AP AP= − =  0m < 0m = 0 1m< < 1m = 1m > 0 1 2 3 4 5 5 5 5 5 5 5C C C C C C 32+ + + + + = 0 0 1 0− + > 0 0 3 0+ − < 2 2 4× = 2 1 4 2 = 1sin cos cos sin sin12 12 12 12 6 2a b π π π π π= + = =   m α⊥ m n⊥ n α α m α⊂ n β⊂ α β m n m α⊂ n α⊂ m β n β α β 【答案】A 【解析】 的坐标为 ，设 P 点坐标为 ， ，解得 ，由 可得 ，则 ，该双曲线为等轴双曲线，离心率为 . 21. 【考查内容】直棱柱的侧面积 【答案】4ah 22.【考查内容】正弦定理 【答案】 【解析】由正弦定理可知， , 23.【考查内容】系统抽样 【答案】42 【解析】从 500 名学生中抽取 50 名，则每两相邻号码之间的间隔是 10，第一个号码是 2， 则第五个号码段中抽取的号码应是 24.【考查内容】椭圆的简单几何性质 【答案】 【解析】圆 的圆心为（3,0），半径为 4，则椭圆的长轴长为 8，即 ， ，则短轴长为 25.【考查内容】不等式的基本性质，集合的交集和并集 【答案】 【解析】∵ ，∴ ；∵ ，∴ ；∴ ， ； 同 理 可 得 ， ∴ . 由 ① ③ 可 得 . 则 ， ， . . 26. 【考查内容】等差数列的实际应用 【解】由题意知各排人数构成等差数列 ，设第一排人数是 ，则公差 ，前 5 项和 ,因为 ，所以 ，解得 . 答：第一排应安排 18 名演员 27.【考查内容】正弦型函数的图象和性质 【解】（1）函数的最小正周期 ,因为函数的图象过点（0,1），所以 ，即 ，又因为 ，所以 . 1F ( ,0)c− 0( , )c y− 22 0 2 2 ( ) 1yc a b − − = 2 0 by a = 1PF a= 2b aa = a b= 2 2+ 6 sin sin AB BC C A = sin 2 2 sin105 6 2sin 2 2 AB ABC C = = = + 2 4 10 42+ × = 2 7 2 2 6 7 0x y x+ − − = 3, 4c a= = 2 2 7b a c= − = 2 7 { }x c x e b x d< <或  a b c d+ < + a c d b− < − a b c d− = − a c b d− = − b d d b− < − b d< d f< b d f< < 0a c e b d f< < < < < < { }A B x c x b= < < { }B C x e x d= < < { }C A x e x b= < < A B C⊗ ⊗ = { }x c x e b x d< <或  { }na 1a 3d = 5 120S = 1 ( 1) 2n n nS na d −= + 1 5 4120 5 32a ×= + × 1 18a = 2 2T π= = π 2sin 1ϕ = 1sin 2 ϕ = 0 2 ϕ π< < 6 ϕ π= (2)因为函数 的单调递增区间是 . 所以 ，解得 ， 所以函数的单调递增区间是 28.【考查内容】指数函数的单调性 【解】（1）当 时，函数 在区间 上是减函数， 所以当 时，函数 取得最大值 16，即 ，所以 . 当 时，函数 在区间 上是增函数， 所以当 时，函数 取得最大值 16，即 ，所以 . （ 2 ） 因 为 的 定 义 域 是 R, 即 恒 成 立 . 所 以 方 程 的判别式 ，即 ，解得 ，又因为 或 ，所以 .代入不等式得 ，即 ，解得 ，所以实数 t 的取值范 围是 . 29.【考查内容】异面直线所成的角，直线与平面垂直的判定和性质 【解】（1）因为 ,所以 即为 SA 与 BC 所成的角，在△SAD 中， ， 又在正方形 ABCD 中 ,所以 ,所以 SA 与 BC 所成角的余弦值是 . (2)因为平面 平面 ABCD，平面 平面 ABCD ,在正方形 ABCD 中， , 所以 平面 SAD,又因为 平面 SAD,所以 . 30.【考查内容】抛物线的定义、标准方程和性质，直线与抛物线的位置关系 【解】（1）由已知条件，可设抛物线的方程为 ，因为点 Q 到焦点 F 的距离是 1， 所以点 Q 到准线的距离是 1，又因为点 Q 到 y 轴的距离是 ，所以 ，解得 ， 所以抛物线方程是 . （2）假设直线 l 的斜率不存在，则直线 l 的方程为 ，与 联立，可解得交点 A、 B 的坐标分别为 ，易得 ，可知直线 OA 与直线 OB 不垂直，不满 足题意，故假设不成立，从而，直线 l 的斜率存在. siny x= [ 2 , 2 ],2 2k k k π π− + π + π ∈Z 2 2 22 6 2k x k π π π− + π + + π  3 6k x k π π− + π + π  [ , ],3 6k k k π π− + π + π ∈Z 0 1a< < ( )f x [ 2,4]− 2x = − ( )f x 2 16a− = 1 4a = 1a > ( )f x [ 2,4]− 4x = ( )f x 4 16a = 2a = 2 2( ) log ( 3 2 )g x x x a= − + 2 3 2 0x x a− + > 2 3 2 0x x a− + = 0∆ < 2( 3) 4 2 0a− − × < 9 8a > 1 4a = 2a = 2a = 2log (1 2 ) 1t−  0 1 2 2t< −  1 1 2 2t− < 1 1[ , )2 2 − AD BC SAD∠ 2SA SD= = 3AD AB= = 2 2 2 2 2 22 3 2cos 2 2 2 3 SA AD SDSAD SA AD + − + −∠ = = × × 3 4 = 3 4 SAD ⊥ SAD  AD= AB AD⊥ AB ⊥ SD ⊂ AB SD⊥ 2 2y px= 3 8 312 8 p = − 5 4p = 2 5 2y x= 3x = 2 5 2y x= 30 30(3, ),(3, )2 2 − 3 2OA OB =   设直线 l 的斜率为 k， 则方程为 ，整理得 ， 设 联立直线 l 与抛物线的方程得 , 消去 y，并整理得 ， 于是 . 由①式变形得 ，代入②式并整理得 ， 于是 ，又因为 ，所以 ，即 ， ，解得 或 . 当 时，直线 l 的方程是 ，不满足 ，舍去. 当 时 ， 直 线 l 的 方 程 是 ， 即 ， 所 以 直 线 l 的 方 程 是 . 1 ( 3)y k x− = − 3 1y kx k= − + 1 1 2 2( , ), ( , ),A x y B x y 2 3 1 5 2 y kx k y x = − + = ① ② 2 2 2 25(6 2 ) 9 6 1 02k x k k x k k− − + + − + = 2 1 2 2 9 6 1k kx x k − += 3 1y kx k + −= 22 5 15 5 0ky y k− − + = 1 2 15 5 2 ky y k − += OA OB⊥ 0OA OB =   1 2 1 2 0x x y y+ =  2 2 9 6 1 15 5 02 k k k kk − + − ++ = 1 3k = 2k = 1 3k = 1 3y x= OA OB⊥ 2k = 1 2( 3)y x− = − 2 5 0x y− − = 2 5 0x y− − =