- 2.46 MB
- 2021-05-13 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
2012届高考数学(理)考前60天冲刺
统计和概率专练
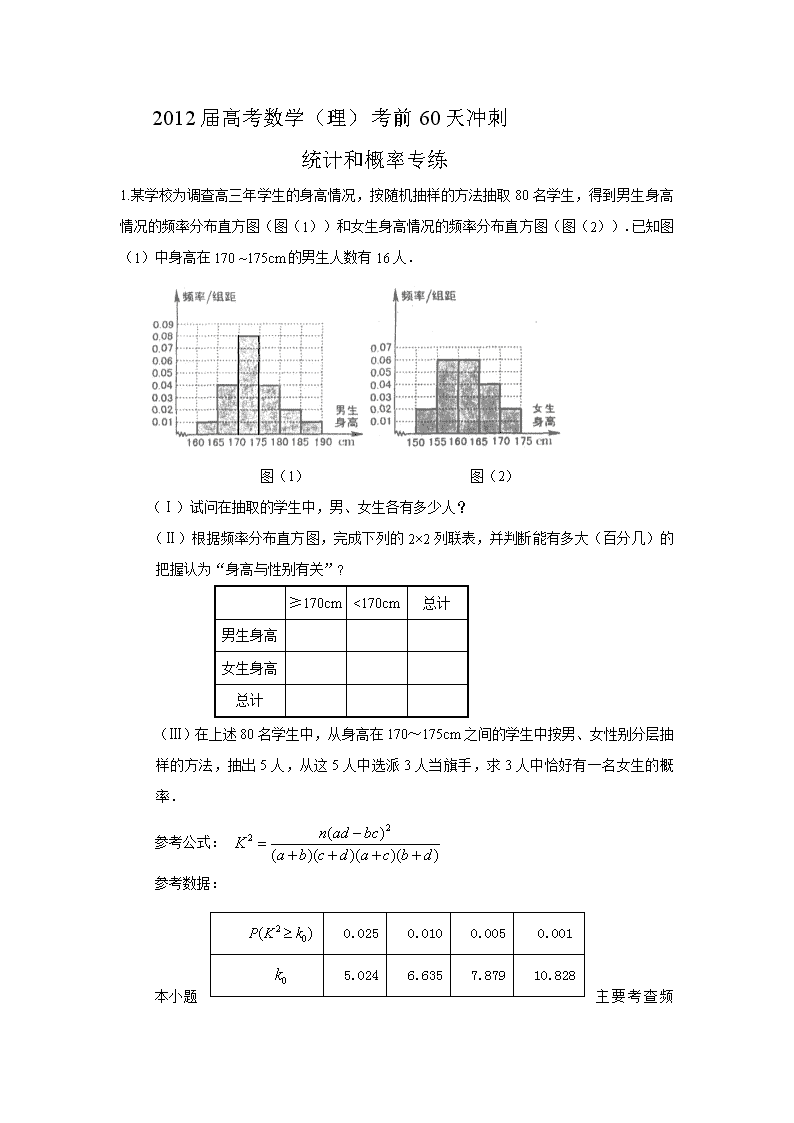
1.某学校为调查高三年学生的身高情况,按随机抽样的方法抽取80名学生,得到男生身高情况的频率分布直方图(图(1))和女生身高情况的频率分布直方图(图(2)).已知图(1)中身高在170 ~175cm的男生人数有16人.
图(1) 图(2)
(Ⅰ)试问在抽取的学生中,男、女生各有多少人?
(Ⅱ)根据频率分布直方图,完成下列的2×2列联表,并判断能有多大(百分几)的把握认为“身高与性别有关”?
≥170cm
<170cm
总计
男生身高
女生身高
总计
(Ⅲ)在上述80名学生中,从身高在170~175cm之间的学生中按男、女性别分层抽样的方法,抽出5人,从这5人中选派3人当旗手,求3人中恰好有一名女生的概率.
参考公式:
参考数据:
0.025
0.010
0.005
0.001
5.024
6.635
7.879
10.828
本小题主要考查
频率分布直方图、列联表和概率等基础知识,考查数据处理能力、运算求解能力以及应用用意识,考查必然与或然思想、分类与整合思想等.满分12分.
解:(Ⅰ)直方图中,因为身高在170 ~175cm的男生的频率为,
设男生数为,则,得.………………………………………4分
由男生的人数为40,得女生的人数为80-40=40.
(Ⅱ)男生身高的人数,女生身高的人数,所以可得到下列列联表:
≥170cm
<170cm
总计
男生身高
30
10
40
女生身高
4
36
40
总计
34
46
80
…………………………………………6分
,………………………………………7分
所以能有99.9%的把握认为身高与性别有关;…………………………………………8分
(Ⅲ)在170~175cm之间的男生有16人,女生人数有人.
按分层抽样的方法抽出5人,则男生占4人,女生占1人. ………………………9分
设男生为,女生为.
从5人任选3名有:
,共10种可能,………………………………10分
3人中恰好有一名女生有:共6种可能,………………………11分
故所求概率为.
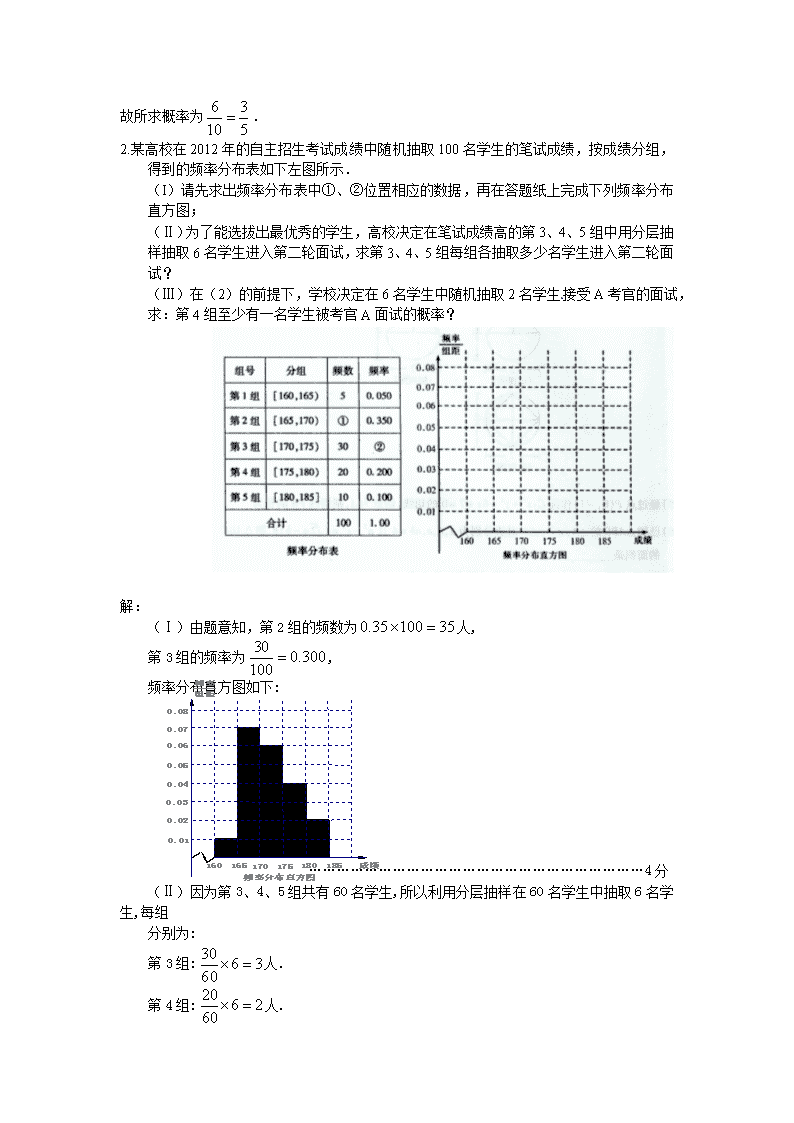
2.某高校在2012年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如下左图所示.
(I)请先求出频率分布表中①、②位置相应的数据,再在答题纸上完成下列频率分布直方图;
(Ⅱ)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试?
(Ⅲ)在(2)的前提下,学校决定在6名学生中随机抽取2名学生接受A考官的面试,求:第4组至少有一名学生被考官A面试的概率?
解:
(Ⅰ)由题意知,第2组的频数为人,
第3组的频率为,
频率分布直方图如下:
………………………………………………………………4分
(Ⅱ)因为第3、4、5组共有60名学生,所以利用分层抽样在60名学生中抽取6名学生,每组
分别为:
第3组:人.
第4组:人.
第5组:人,
所以第3、4、5组分别抽取3人、2人、1人.…………………………………………8分
(Ⅲ)设第3组的3位同学为,第4组的2位同学为,第5组的1位同学为,
则从六位同学中抽两位同学有15种可能如
下:
其中第4组的2位同学至少有一位同学
入选的有:
共9种.
所以其中第4组的2位同学至少有一位同学入选的概率为
3.对某校高三年级学生参加社区服务次数进行统计,
随机抽取名学生作为样本,得到这名学生参加社区服务的次数. (第18题图)
根据此数据作出了频数与频率的统计表和频率分布直方图如下:
分组
频数
频率
24
4
0.1
2
0.05
合计
1
频率/组距
15
25
20
10
0
30
次数
a
(Ⅰ)求出表中及图中的值;
(Ⅱ)若该校高三学生有240人,试估计该校高三学生参加社区服务的次数在区间 内的人数;
(Ⅲ)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至多一人参加社区服务次数在区间内的概率.
解(Ⅰ)由分组内的频数是4,频率是0.1知,,所以
因为频数之和为,所以,.---4分
因为是对应分组的频率与组距的商,所以----------6分
(Ⅱ)因为该校高三学生有240人,分组内的频率是,
所以估计该校高三学生参加社区服务的次数在此区间内的人数为人. ……----8分
(Ⅲ)这个样本参加社区服务的次数不少于20次的学生共有人,
设在区间内的人为,在区间内的人为.
则任选人共有
,15种情况, ……10分
而两人都在内只能是一种,所以所求概率为
5.某日用品按行业质量标准分成五个等级,等级系数X依次为1,2,3,4,5.现从一批该日用品中随机抽取20件,对其等级系数进行统计分析,得到频率分布表如下:
X
1
2
3
4
5
频率
a
0.2
0.4
b
c
(I)若所抽取的20件日用品中,等级系数为4的恰有3件,等级系数为5的恰有2件,求a,b,c的值;
(Ⅱ)在(I)的条件下,将等级系数为4的3件日用品记为x1,x2,x3,等级系数为5的2件日用品记为y1,y2,现从x1,x2,x3,y1,y2这5件日用品中任取两件(假定每件日用品被取出的可能性相同),写出所有可能的结果,并求这两件日用品的等级系数恰好相等的概率.
解:(Ⅰ)由频率分布表得a+0.2+0.45+b+c=1,即a+b+c=0.35.
因为抽取的20件日用品中,等级系数为4的恰有3件,所以b==0.15.
等级系数为5的恰有2件,所以c==0.1.
从而a=0.35-b-c=0.1.
所以a=0.1,b=0.15,c=0.1. ………………6分
(Ⅱ)从日用品x1,x2,x3,y1,y2中任取两件,所有可能的结果为:
{x1,x2},{x1,x3},{x1,y1},{x1,y2},{x2,x3},{x2,y1},{x2,y2},{x3,y1},{x3,y2},{y1,y2}.
设事件A表示“从日用品x1,x2,x3,y1,y2中任取两件,其等级系数相等”,则A包含的基本事件为:
{x1,x2},{x1,x3},{x2,x3},{y1,y2},共4个.
又基本事件的总数为10,
故所求的概率P(A)==0.4. ………………12分
6. 已知A、B、C三个箱子中各装有2个完全相同的球,每个箱子里的球,有一个球标着号码1,另一个球标着号码2,现从A、B、C三个箱子中各摸出1个球。
(1)若用数组(x,y,z)中的x、y、z分别表示从A、B、C三个箱子中摸出的球的号码,请写出数组(x,y,z)的所有情形,并回答一共有多少种;
(2)如果请您猜测摸出的这三个球的号码之和,猜中有奖,那么猜什么数获奖的可能性最大?请说明理由。
(1)解:数组(x,y,z)的所有情形为:(1,1,1),(1,1,2),(1,2,1),(1,2,2),(2,1,1),(2,1,2),(2,2,1),(2,2,2),共8种 6分
注:列出所有情形,得6分,列出5种以上情形,得4分.
(2)解:摸出的三个球号码的和可能为3,4,5,6,故记“所摸出的三个球号码之和为i”为事件Ai (i = 3,4,5,6) 8分
易知,事件A3包含有1个基本事件,事件A4包含有3个基本事件,事件A5包含有3个基本事件,事件A6包含有1个基本事件 10分
∴
7.为了淮北市争创“全国文明城市”,市文明委组织了精神文明建设知识竞赛。 统计局调查中心随机抽取了甲.乙两队中各6名组员的成绩,得分情况如下表所示:
甲组
84
85
87
88
88
90
乙组
82
86
87
88
89
90
(1)根据表中的数据,哪个组对精神文明建设知识的掌握更为稳定?
(2)用简单随机抽样方法从乙组6名成员中抽取两名,他们的得分情况组成一个样本,求抽出的两名成员的分数差值至少是4分的概率。
解析:(1)由题意可知,
, ………………1分
………………2分
……3分
……4分
因为,所以甲组的成绩比乙组稳定。 ………6分
(2)从乙组抽取两名成员的分数,所有基本事件为(用坐标表示):(82,86),(82,87),(82,87),(82,89),(82,90),(86,87),(86,88),(86,89),(86,90),(87,88)(87,89)(87,90),(88,89),(88,90),(89,90)共15种情况。 ………………8分
则抽取的两名成员的分数差值至少是4的事件包含:(82,86),(82,87),(82,87),(82,89),(82,90),(86,90)共6种情况。 ………………10分
由古典概型公式可知,抽取的两名成员的分数差值至少是4分的概率P=
8.某研究性学习小组对春季昼夜温差大小与某花卉种子发芽多少之间的关系进行研究,他们分别记录了3月1日至3月5日的每天昼夜温差与实验室每天每100颗种子浸泡后的发芽数,得到如下资料:
日期
3月1日
3月2日
3月3日
3月4日
3月5日
温差x(oC)
10
11
13
12
8
发芽数y(颗)
23
25
30
26
16
(I)从3月1日至3月5日中任选2天,记发芽的种子数分别为m,n,求事件“m,n均小于25”的概率;
(II)请根据3月2日至3月4日的数据,求出y关于x的线性回归方程;
(III)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(II)所得的线性回归方程是否可靠?
(参考公式:回归直线方程式,其中)
(I)m,n构成的基本事件(m,n)有:(23,25),(23,30),(23,26),(23,16),(25,30),(25,26),(25,16),(30,26),(30,16),(26,16),共有10个.
………………………………………………………………2分
其中“m,n均小于25”的有1个,其概率为. ………………………4分
(II)∵
∴. ………………………6分
于是,. ……………………………………………8分
故所求线性回归方程为. …………………………………………9分
(III)由(2)知,
当x=10时,y=22;当x=8时,y=17. ………………………………………11分
与检验数据的误差均为1,满足题意.
故认为得到的线性回归方程是可靠的.
9.在甲、乙两个盒子中分别装有标号为1、2、3、4的四个球,现从甲、乙两个盒子中各取出1个球,每个小球被取出的可能性相等。
(1)求取出的两个球上标号为相邻整数的概率;
(2)求取出的两个球上标号之和能被3整除的概率.
(Ⅰ)当时,~.--------------------------3分
故,. ---------6分
(Ⅱ)的可取值为.
;
;
--------------------10分
的分布列为
0
1
2
3
P
----------------------12分
10. 为了解学生喜欢数学是否与性别有关,对50个学生进行了问卷调查得到了如下的列联表:
喜欢数学
不喜欢数学
合计
男生
5
女生
10
合计
50
已知在全部50人中随机抽取1人抽到喜欢数学的学生的概率为.
(1)请将上面的列联表补充完整(不用写计算过程);
(2)是否有99.5%的把握认为喜欢数学与性别有关?说明你的理由;
下面的临界值表供参考:
0.15
0.10
0.05
0.025
0.010
0.005
0.001
2.072
2.706
3.841
5.024
6.635
7.879
10.828
(参考公式:,其中)
.解:解:(1) 列联表补充如下:
喜爱数学
不喜爱数学
合计
男生
20
5
25
女生
10
15
25
合计
30
20
50
------5分
(2)∵------------------------10分
∴有99.5%的把握认为喜爱数学与性别有关.---------------------12分
11.
O
60 65 70 75 80 85 疱疹面积
0.03
0.04
0.05
0.06
注射药物B后皮肤疱疹面积频率分布直方图
注射药物A后皮肤疱疹面积的频数分布表
疱疹面积
频数
20
50
20
10
为了比较注射两种药物后产生的皮肤疱疹的面积,选200只老鼠做试验,将这200只老鼠随机地分成两组,每组100只,其中一组注射药物(称为组),另一组注射药物(称为组),则两组老鼠皮肤疱疹面积(单位:)的频率分布表、频率分布直方图分别如下.
(Ⅰ)为方便两组试验对比,现都用分层抽样方法从
两组中各挑出20只老鼠,求两组成肤疱疹
面积同为的这一区间应分别挑出几只?
(Ⅱ)在(Ⅰ)的条件下,将两组挑出的皮肤疱疹面积
同为这一区间上的老鼠放在一起观察,几天
后,从中抽取两只抽血化验,求组中至少有1只被
抽中的概率.
【解】(Ⅰ)由组频数分布表可知,组中这一小组的频数为20,………1分
由组频率分布直方图可知,组中这一小组的频率为
…………………3分
所以这一小组频数为……………………4分
由于是分层抽样,所以,…………………5分
即两组中成肤疱疹面积同为的这一区间应分别挑出4只、2只………6分
(Ⅱ)由(Ⅰ)知,两组中这一区间上挑出的老鼠分别有4只、2只,
设编号分别为1,2,3,4;5(组),6(组), …………………7分
则从中抽取两只的所有基本事件如下
(1,2), (1,3), (1,4), (1,5), (1,6); (2,3), (2,4), (2,5),(2,6); (3,4), (3,5),(3,6); (4,5),(4,6); (5,6)
共有15个……………………………………8分
显然事件{组中至少有1只被抽中}发生包含了以下9个基本事件,
(1,5), (1,6); (2,5),(2,6); (3,5),(3,6); (4,5),(4,6); (5,6)……………10分
所以由古典概型知
12.已知集合在平面直角坐标系中,点M(x,y)的坐标。
(1)请列出点M的所有坐标;
(2)求点M不在x轴上的概率;
(3)求点M正好落在区域上的概率。
解:(1)集合A={-2,0,1,3},点M(x,y)的坐标,
点M的坐标共有:个,分别是:
(-2,-2),(-2,0),(-2,1),(-2,3);(0,-2),(0,0),(0,1),(0,3);
(1,-2),(1,0),(1,1),(1,3);(3,-2),(3,0),(3,1),(3,3)…………………….4分
(2)点M不在x轴上的坐标共有12种:
(-2,-2),(-2,0),(-2,1),(-2,3);(1,-2),(1,0),(1,1),(1,3);
(3,-2),(3,0),(3,1),(3,3)
所以点M不在x轴上的概率是………………………………………..8分
(3)点M正好落在区域上的坐标共有3种:(1,1),(1,3),(3,1)
故M正好落在该区域上的概率为
13.中华人民共和国道路交通安全法》规定:车辆驾驶员血液酒精浓度在20~80 mg/100 ml(不含80)之间,属于酒后贺车;在80 mg /100 ml (含80)以上时,属醉酒贺车,对于酒后驾车和醉酒驾车的驾驶员公安机关将给予不同程度的处罚.
某市公安局交通管理部门在某路段的一次拦查行动中,依法检查了250辆机动车,查出酒后驾车和醉酒贺车的驾驶员20人,下图是对这20人血液中酒精含量进行检查所得结果的频率分布直方图.
(1)根据频率分布直方图,求:此次抽查的250人中,醉酒驾车的人数;
(2)从血液酒精浓度在[70,90)范围内的驾驶员中任取2人,求恰有1人属于醉酒驾车的概率.
解: (1)
酒精含量(单位:mg/100ml)
[20,30)
[30,40)
[40,50)
[50,60)
人数
3
4
4
1
酒精含量(单位:mg/100ml)
[60,70)
[70,80)
[80,90)
[90,100]
人数
2
3
2
1
所以醉酒驾车的人数为人………………………………………………6分
(2)因为血液酒精浓度在[70,80)内范围内应抽3人,记为a,b,c, [80,90)范围内有2人,记为d,e,则从中任取2人的所有情况为(a,b),(a,c),(a,d),(a,e),(b,c),(b,d),(b,e),(c,d),(c,e),(d,e),共10种…………………………………………….8分
恰有一人的血液酒精浓度在[80,90)范围内的情况有(a,d),(a,e),(b,d),(b,e),(c,d),(c,e),共6种,……………………………………………………………………….10分
设“恰有1人属于醉酒驾车”为事件A,则P(A)==.……
14. 是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.我国标准采用世卫组织设定的最宽限值,日均值在35微克/立方米以下空气质量为一级;在35微克/立方米75微克/立方米之间空气质量为二级;在75微克/立方米及其以上空气质量为超标.
某试点城市环保局从该市市区2011年全年每天的监测数据中随机抽取6天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶),若从这6天的数据中随机抽出2天.
(Ⅰ)求恰有一天空气质量超标的概率;
(Ⅱ)求至多有一天空气质量超标的概率.
解: 由茎叶图知:6天有4天空气质量未超标,有2天空气质量超标. …………2分
记未超标的4天为,超标的两天为.则从6天中抽取2天的所有情况为:,,,,,,,,,,,,,,,基本事件数为15.…………4分
(Ⅰ)记 “6天中抽取2天,恰有1天空气质量超标”为事件,可能结果为:,,,,,,,,基本事件数为.
∴;……………6分
(Ⅱ)记“至多有一天空气质量超标”为事件,
“2天都超标”为事件,其可能结果为,…………………………8分
故,…………………………………………………………10分
∴.
15.为加强中学生实践、创新能力和团队精神的培养,促进教育教学改革,郑州市教育局举办了全市中学生创新知识竞赛.某校举行选拔赛,共有200名学生参加,为了解成绩情况,从中抽取50名学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成的频率分布表,解答下列问题:
(I)若用系统抽样的方法抽取50个样本,现将所有学生随机地编号为000,001,002,…,199,试写出第二组第一位学生的编号;
(II) 求出a,b,c,d,e的值(直接写出结果),并作出频率分布直方图;
(III)若成绩在85.5〜95. 5分的学生为二等奖,问参赛学生中获得二等奖的学生约为多少人?
[解析] (Ⅰ)编号为004. ……3分
(Ⅱ) a,b,c,d,e的值分别为
13, 4, 0.30, 0.08, 1.…… ……8分
(Ⅲ)在被抽到的学生中获二等奖的人数
9+2=11(人),占样本的比例是=0.22,
即获二等奖的概率为22%,所以获二等奖
的人数估计为200×22%=44(人).
答:获二等奖的大约有44人.……12分
16.某日用品按行业质量标准分成五个等级,等级系数X依次为1,2,3,4,5.现从一批该日用品中随机抽取20件,对其等级系数进行统计分析,得到频率分布表如下:
X
1
2
3
4
5
频率
a
0.2
0.4
b
c
(I)若所抽取的20件日用品中,等级系数为4的恰有3件,等级系数为5的恰有2件,求a,b,c的值;
(Ⅱ)在(I)的条件下,将等级系数为4的3件日用品记为x1,x2,x3,等级系数为5的2件日用品记为y1,y2,现从x1,x2,x3,y1,y2这5件日用品中任取两件(假定每件日用品被取出的可能性相同),写出所有可能的结果,并求这两件日用品的等级系数恰好相等的概率.
解:(Ⅰ)由频率分布表得a+0.2+0.45+b+c=1,即a+b+c=0.35.
因为抽取的20件日用品中,等级系数为4的恰有3件,所以b==0.15.
等级系数为5的恰有2件,所以c==0.1.
从而a=0.35-b-c=0.1.
所以a=0.1,b=0.15,c=0.1. ………………6分
(Ⅱ)从日用品x1,x2,x3,y1,y2中任取两件,所有可能的结果为:
{x1,x2},{x1,x3},{x1,y1},{x1,y2},{x2,x3},{x2,y1},{x2,y2},{x3,y1},{x3,y2},{y1,y2}.
设事件A表示“从日用品x1,x2,x3,y1,y2中任取两件,其等级系数相等”,则A包含的基本事件为:
{x1,x2},{x1,x3},{x2,x3},{y1,y2},共4个.
又基本事件的总数为10,
故所求的概率P(A)==0.4.
17. 已知A、B、C三个箱子中各装有2个完全相同的球,每个箱子里的球,有一个球标着号码1,另一个球标着号码2,现从A、B、C三个箱子中各摸出1个球。
(1)若用数组(x,y,z)中的x、y、z分别表示从A、B、C三个箱子中摸出的球的号码,请写出数组(x,y,z)的所有情形,并回答一共有多少种;
(2)如果请您猜测摸出的这三个球的号码之和,猜中有奖,那么猜什么数获奖的可能性最大?请说明理由。
(1)解:数组(x,y,z)的所有情形为:(1,1,1),(1,1,2),(1,2,1),(1,2,2),(2,1,1),(2,1,2),(2,2,1),(2,2,2),共8种 6分
注:列出所有情形,得6分,列出5种以上情形,得4分.
(2)解:摸出的三个球号码的和可能为3,4,5,6,故记“所摸出的三个球号码之和为i”为事件Ai (i = 3,4,5,6) 8分
易知,事件A3包含有1个基本事件,事件A4包含有3个基本事件,事件A5包含有3个基本事件,事件A6包含有1个基本事件 10分
∴
18.有关部门要了解甲型H1N1流感预防知识在学校的普及情况,命制了一份有道题的问卷到各学校做问卷调查.某中学两个班各被随机抽取名学生接受问卷调查,班名学生得分为:,,,,;班5名学生得分为:,,,,.
(Ⅰ)请你估计两个班中哪个班的问卷得分要稳定一些;
(Ⅱ)如果把班名学生的得分看成一个总体,并用简单随机抽样方法从中抽取样本容量为的样本,求样本平均数与总体平均数之差的绝对值不小于的概率.
解:(Ⅰ)∵班的名学生的平均得分为÷, ………1分
方差;……3分
班的名学生的平均得分为÷, ……………………4分
方差. ……6分
∴ ,
∴ 班的预防知识的问卷得分要稳定一些. …………………………8分
(Ⅱ)从班名同学中任选名同学的方法共有种, …………………10分
其中样本和,和,和,和的平均数满足条件,故所求概率为.
19.近年来,我国机动车拥有量呈现快速增加的趋势,可与之配套的基础设施建设速度相对迟缓,交通拥堵问题已经成为制约城市发展的重要因素,为了解某市的交通状况,现对其6条道路进行评估,得分分别为5、6、7、8、9、10规定评估的平均得分与全市的总体交通状况等级如下表:
评估的平均得分
[0,6]
[6,8]
[8,10]
全市的总体交通
不合格
合格
优秀
(1)求本次评估的平均得分,并参照上表估计该市的总体交通状况等级。
(2)用简单随机抽样方法从6条道路中抽取2条,它们的得分组成一个样本,求该样本的平均数与总体的平均数之差的绝对值不超过0.5的概率。
解:(1)合格---------------------6分
(2)基本事件为(5,6)(5,7)(5,8)(5,9)(5,10)(6,7)(6,8)(6,9)(6,10)(7,8)(7,9)(7,10) (8,9)(8,10)(9,10)共15个
19.(本小题满分12分)
一工厂生产甲, 乙, 丙三种样式的杯子,每种样式均有500ml和700ml两种型号,
某天的产量如右表(单位:个):
型号
甲样式
乙样式
丙样式
500ml
2000
z
3000
700ml
3000
4500
5000
按样式进行分层抽样,在该天生产的杯子中抽取100个,其中有甲样式杯子25个.
(I)求z的值;
(II)用分层抽样的方法在甲样式杯子中抽取一个容量为5的样本,从这个样本中任取2个杯子,求至少有1个500ml杯子的概率.
解: (I)设该厂本月生产的乙样式的杯子为n个,在丙样式的杯子中抽取x个,由题意得, ,所以x=40. -----------2分
则100-40-25=35,所以,n=7000,
故z=2500 ----------6分
(II)设所抽样本中有m个500ml杯子,
因为用分层抽样的方法在甲样式杯子中抽取一个容量为5的样本,
所以,解得m=2 -----------9分
也就是抽取了2个500ml杯子,3个700ml杯子,分别记作S1,S2;B1,B2,B3,则从中任取2个的所有基本事件为(S1, B1), (S1, B2) , (S1, B3) (S2 ,B1), (S2 ,B2), (S2 ,B3),( (S1, S2),(B1 ,B2), (B2 ,B3) ,(B1 ,B3)共10个,其中至少有1个500ml杯子的基本事件有7个基本事件:
(S1, B1), (S1, B2) , (S1, B3) (S2 ,B1), (S2 ,B2), (S2 ,B3),( (S1, S2),所以从中任取2个,
至少有1个500ml杯子的概率为.
20.一化工厂因排污趋向严重,2011年1月决定着手整治。经调研,该厂第一个月的污染度为,整治后前四个月的污染度如下表;
月数
1
2
3
4
……
污染度
60
31
13
0
……
污染度为后,该工厂即停止整治,污染度又开始上升,现用下列三个函数模拟从整治后第一个月开始工厂的污染模式:
,,,其中表示月数,分别表示污染度.
(参考数据:)
(Ⅰ)问选用哪个函数模拟比较合理,并说明理由;
(Ⅱ)如果环保部门要求该厂每月的排污度均不能超过60,若以比较合理的模拟函数预测,该厂最晚在何时开始进行再次整治?
(Ⅰ) …………3分
…………6分
由此可得更接近实际值,所以用模拟比较合理. …………7分
(Ⅱ)因在上是增函数,又因为 ………12分
这说明第一次整治后有16个月的污染度不超过60,
故应在2012年5月起开始再次整治.
21. 某校高三年级共有450名学生参加英语口语测试,其中男生250名,女生200名。现按性别用分层抽样的方法从中抽取45名学生的成绩。
(I)求抽取的男生与女生的人数?
(II)从男生和女生中抽查的结果分别如下表1和表2;
表1
成绩分组
人数
3
m
8
6
表2
成绩分组
人数
2
5
n
5
分别估计男生和女生的平均分数,并估计这450名学生的平均分数。(精确到0.01)
解析:(Ⅰ)由抽样方法知,被抽取的男生人数为250×=25,
被抽取的女生人数为200×=20.……………………………………………2分
(Ⅱ)男生甲和女生乙被抽到的概率均为0.1,所以男生甲与女生乙至少有1人被抽到的概率:P=1-(1-0.1)2=0.19.……………………………………………………………7分
(Ⅲ)由(Ⅰ)知,m=25-(3+8+6)=8,n=20-(2+5+5)=8,据此估计
男生平均分为=81.8,
女生平均分为=83;
这450名学生的平均分数为≈82.33.
22. 设平顶向量= ( m , 1), = ( 2 , n ),其中 m, n {1,2,3,4}.
(I)请列出有序数组( m,n )的所有可能结果;
(II)记“使得(-)成立的( m,n )”为事件A,求事件A发生的概率。
(II)由得,即。由于,故事件A包含的基本事件为(2,1)和(3,4),共2个。又基本事件的总数为16,故所求的概率为。……………………12
23.
某校高一某班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下,据此解答如下问题:
(1)求分数在[50,60)的频率及全班人数;
(2)求分数在[80,90)之间的频数,并计算频率分布直方图中[80,90)间的矩形的高;
(3)若要从分数在[80,100]之间的试卷中任取两份分析学生失分情况,在抽取的试卷中,求至少有一份分数在[90,100]之间的概率.
解:(1)分数在[50,60)的频率为0.008×10=0.08,(2分)
由茎叶图知:分数在[50,60)之间的频数为2,所以全班人数为=25,(4分)
(2)分数在[80,90)之间的频数为25-2-7-10-2=4;(6分)
频率分布直方图中[80,90)间的矩形的高为÷10=0.016.(8分)
(3)将[80,90)之间的4个分数编号为1,2,3,4,[90,100]之间的2个分数编号为5,6,
在[80,100]之间的试卷中任取两份的基本事件为:
(1,2),(1,3),(1,4),(1,5),(1,6),
(2,3),(2,4),(2,5),(2,6),
(3,4),(3,5),(3,6),
(4,5),(4,6),
(5,6)共15个,(10分)
其中,至少有一个在[90,100]之间的基本事件有9个,
故至少有一份分数在[90,100]之间的概率是=0.6.(12分)
24.甲乙二人用4张扑克牌(分别是红桃2, 红桃3, 红桃4, 方片4)玩游戏,他们将扑克牌洗匀后,背面朝上放在桌面上,甲先抽,乙后抽,抽出的牌不放回,各抽一张.
(1)设分别表示甲、乙抽到的牌,写出甲乙二人抽到的牌的所有情况.
(2)若甲 抽到红桃3,则乙抽出的牌的牌面数字比3大的概率是多少?
(3)甲乙约定:若甲抽到的牌面数字比乙大,则甲胜,反之,则乙胜。你认为此游戏是否公平,说明你的理由。
26. 某车间在两天内,每天生产10件某产品,其中第一天、第二天分别生产出了1件、2件次品.而质检部门每天要从生产的10件产品中随意抽取4件进行检查,若发现有次品,则当天的产品不能通过.
(Ⅰ)求第一天产品通过检查的概率;
(Ⅱ)(文)求两天全部通过的概率.
(解:(Ⅰ)∵随意抽取4件产品检查是随机事件,而第一天有9件正品.
∴第一天通过检查的概率为. ……………………………4分
(Ⅱ)同(Ⅰ),第二天通过检查的概率为. …………………9分
因第一、第二天是否通过检查相互独立, ……………………………10分
所以,两天全部通过检查的概率为. …………12分
27.某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究,他们分别记录了12月1日至12月5日的每天昼夜温差与实验室每天每100颗种子中的发芽数,得到如下资料:
日 期
12月1日
12月2日
12月3日
12月4日
12月5日
温差x(°C)
10
11
13
12
8
发芽数y(颗)
23
25
30
26
16
该农科所确定的研究方案是:先从这五组数据中选取2组,用剩下的3组数据求线性回归方程,再对被选取的2组数据进行检验.
(1)求选取的2组数据恰好是不相邻2天数据的概率;
(2)若选取的是12月1日与12月5日的两组数据,请根据12月2日至12月4日的数据,求出y关于x的线性回归方程;并预报当温差为9 0C时的种子发芽数。
解:(1)设抽到不相邻的两组数据为事件A,从5组数据中选取2组数
据共有10种情况:(1,2)(1,3)(1,4)(1,5)(2,3)
(2,4)(2,5)(3,4)(3,5)(4,5),
····················3分
其中数据为12月份的日期数.每种情况都是可能出现的,
事件A包括的基本事件有6种.
∴P(A)=
∴选取的2组数据恰好是不相邻2天数据的概率是
····················6分
(2)由数据,求得 .
····················8分
由公式,求得b=
∴y关于x的线性回归方程为x-3.
····················10分
由此可以预报当温差为9 0C时的种子发芽数为19或20颗
····················12分
28.现从3道选择题和2道填空题中任选2题.
(Ⅰ)求选出的2题都是选择题的概率;(Ⅱ)求选出的两题中至少1题是选择题的概率.
解(Ⅰ)记“选出两道都是选择题”为A,5题任选2题,共有种,
其中,都是选择题有3种.……………2分 ∴ .………………………4分
(Ⅱ).记“选出1道选择题,1道填空题”为B,
∴ ……………………………10分
所以,至少有1道选择题的概率 ……………12分
29.先后随机投掷2枚正方体骰子,其中表示第枚骰子出现的点数,表示第枚骰子出现的点数. (Ⅰ)求点在直线上的概率; (Ⅱ)求点满足的概率.
解:(Ⅰ)每颗骰子出现的点数都有种情况,
所以基本事件总数为个. …………………… 2分
记“点在直线上”为事件,有5个基本事件:
, …………………… 5分
…………………… 6分
(Ⅱ)记“点满足”为事件,则事件有个基本事件:
当时,当时,; …………………… 7分
当时,;当时, …………………… 9分
当时,;当时,. 11分 12分
30.有两个不透明的箱子,每个箱子都装有4个完全相同的小球,球上分别标有数字1、2、3、4.
(Ⅰ)甲从其中一个箱子中摸出一个球,乙从另一个箱子摸出一个球,谁摸出的球上标的数字大谁就获胜(若数字相同则为平局),求甲获胜的概率;(Ⅱ
)摸球方法与(Ⅰ)同,若规定:两人摸到的球上所标数字相同甲获胜,所标数字不相同则乙获胜,这样规定公平吗?
解:(Ⅰ)用(表示甲摸到的数字,表示乙摸到的数字)表示甲、乙各摸一球构成的基本事件,则基本事件有:、、、、、、、、、、、、、、、,共16个; -------------------3分
设:甲获胜的的事件为A,则事件A包含的基本事件有:、、、、、,共有6个;则 ------------------------------5分 ------------------------------6分
(Ⅱ)设:甲获胜的的事件为B,乙获胜的的事件为C;事件B所包含的基本事件有:、、、,共有4个;则 -------------------------8分
----------------------10分
,所以这样规定不公平. -----------------11分
答:(Ⅰ)甲获胜的概率为;(Ⅱ)这样规定不公平. -----------------------12分
2012届高考数学(理)考前60天冲刺【六大解答题】
统计和概率专练
1.某学校为调查高三年学生的身高情况,按随机抽样的方法抽取80名学生,得到男生身高情况的频率分布直方图(图(1))和女生身高情况的频率分布直方图(图(2)).已知图(1)中身高在170 ~175cm的男生人数有16人.
图(1) 图(2)
(Ⅰ)试问在抽取的学生中,男、女生各有多少人?
(Ⅱ)根据频率分布直方图,完成下列的2×2列联表,并判断能有多大(百分几)的把握认为“身高与性别有关”?
≥170cm
<170cm
总计
男生身高
女生身高
总计
(Ⅲ)在上述80名学生中,从身高在170~175cm之间的学生中按男、女性别分层抽样的方法,抽出5人,从这5人中选派3人当旗手,求3人中恰好有一名女生的概率.
参考公式:
参考数据:
0.025
0.010
0.005
0.001
5.024
6.635
7.879
10.828
本小题主要考查频率分布直方图、列联表和概率等基础知识,考查数据处理能力、运算求解能力以及应用用意识,考查必然与或然思想、分类与整合思想等.满分12分.
解:(Ⅰ)直方图中,因为身高在170 ~175cm的男生的频率为,
设男生数为,则,得.………………………………………4分
由男生的人数为40,得女生的人数为80-40=40.
(Ⅱ)男生身高的人数,女生身高的人数,所以可得到下列列联表:
≥170cm
<170cm
总计
男生身高
30
10
40
女生身高
4
36
40
总计
34
46
80
…………………………………………6分
,………………………………………7分
所以能有99.9%的把握认为身高与性别有关;…………………………………………8分
(Ⅲ)在170~175cm之间的男生有16人,女生人数有人.
按分层抽样的方法抽出5人,则男生占4人,女生占1人. ………………………9分
设男生为,女生为.
从5人任选3名有:
,共10种可能,………………………………10分
3人中恰好有一名女生有:共6种可能,………………………11分
故所求概率为.
2.某高校在2012年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如下左图所示.
(I)请先求出频率分布表中①、②位置相应的数据,再在答题纸上完成下列频率分布直方图;
(Ⅱ)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试?
(Ⅲ)在(2)的前提下,学校决定在6名学生中随机抽取2名学生接受A考官的面试,求:第4组至少有一名学生被考官A面试的概率?
解:
(Ⅰ)由题意知,第2组的频数为人,
第3组的频率为,
频率分布直方图如下:
………………………………………………………………4分
(Ⅱ)因为第3、4、5组共有60名学生,所以利用分层抽样在60名学生中抽取6名学生,每组
分别为:
第3组:人.
第4组:人.
第5组:人,
所以第3、4、5组分别抽取3人、2人、1人.…………………………………………8分
(Ⅲ)设第3组的3位同学为,第4组的2位同学为,第5组的1位同学为,
则从六位同学中抽两位同学有15种可能如
下:
其中第4组的2位同学至少有一位同学
入选的有:
共9种.
所以其中第4组的2位同学至少有一位同学入选的概率为
3.对某校高三年级学生参加社区服务次数进行统计,
随机抽取名学生作为样本,得到这名学生参加社区服务的次数. (第18题图)
根据此数据作出了频数与频率的统计表和频率分布直方图如下:
分组
频数
频率
24
4
0.1
2
0.05
合计
1
频率/组距
15
25
20
10
0
30
次数
a
(Ⅰ)求出表中及图中的值;
(Ⅱ)若该校高三学生有240人,试估计该校高三学生参加社区服务的次数在区间 内的人数;
(Ⅲ)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至多一人参加社区服务次数在区间内的概率.
解(Ⅰ)由分组内的频数是4,频率是0.1知,,所以
因为频数之和为,所以,.---4分
因为是对应分组的频率与组距的商,所以----------6分
(Ⅱ)因为该校高三学生有240人,分组内的频率是,
所以估计该校高三学生参加社区服务的次数在此区间内的人数为人. ……----8分
(Ⅲ)这个样本参加社区服务的次数不少于20次的学生共有人,
设在区间内的人为,在区间内的人为.
则任选人共有
,15种情况, ……10分
而两人都在内只能是一种,所以所求概率为
5.某日用品按行业质量标准分成五个等级,等级系数X依次为1,2,3,4,5.现从一批该日用品中随机抽取20件,对其等级系数进行统计分析,得到频率分布表如下:
X
1
2
3
4
5
频率
a
0.2
0.4
b
c
(I)若所抽取的20件日用品中,等级系数为4的恰有3件,等级系数为5的恰有2件,求a,b,c的值;
(Ⅱ)在(I)的条件下,将等级系数为4的3件日用品记为x1,x2,x3,等级系数为5的2件日用品记为y1,y2,现从x1,x2,x3,y1,y2这5件日用品中任取两件(假定每件日用品被取出的可能性相同),写出所有可能的结果,并求这两件日用品的等级系数恰好相等的概率.
解:(Ⅰ)由频率分布表得a+0.2+0.45+b+c=1,即a+b+c=0.35.
因为抽取的20件日用品中,等级系数为4的恰有3件,所以b==0.15.
等级系数为5的恰有2件,所以c==0.1.
从而a=0.35-b-c=0.1.
所以a=0.1,b=0.15,c=0.1. ………………6分
(Ⅱ)从日用品x1,x2,x3,y1,y2中任取两件,所有可能的结果为:
{x1,x2},{x1,x3},{x1,y1},{x1,y2},{x2,x3},{x2,y1},{x2,y2},{x3,y1},{x3,y2},{y1,y2}.
设事件A表示“从日用品x1,x2,x3,y1,y2中任取两件,其等级系数相等”,则A包含的基本事件为:
{x1,x2},{x1,x3},{x2,x3},{y1,y2},共4个.
又基本事件的总数为10,
故所求的概率P(A)==0.4. ………………12分
6. 已知A、B、C三个箱子中各装有2个完全相同的球,每个箱子里的球,有一个球标着号码1,另一个球标着号码2,现从A、B、C三个箱子中各摸出1个球。
(1)若用数组(x,y,z)中的x、y、z分别表示从A、B、C三个箱子中摸出的球的号码,请写出数组(x,y,z)的所有情形,并回答一共有多少种;
(2)如果请您猜测摸出的这三个球的号码之和,猜中有奖,那么猜什么数获奖的可能性最大?请说明理由。
(1)解:数组(x,y,z)的所有情形为:(1,1,1),(1,1,2),(1,2,1),(1,2,2),(2,1,1),(2,1,2),(2,2,1),(2,2,2),共8种 6分
注:列出所有情形,得6分,列出5种以上情形,得4分.
(2)解:摸出的三个球号码的和可能为3,4,5,6,故记“所摸出的三个球号码之和为i”为事件Ai (i = 3,4,5,6) 8分
易知,事件A3包含有1个基本事件,事件A4包含有3个基本事件,事件A5包含有3个基本事件,事件A6包含有1个基本事件 10分
∴
7.为了淮北市争创“全国文明城市”,市文明委组织了精神文明建设知识竞赛。 统计局调查中心随机抽取了甲.乙两队中各6名组员的成绩,得分情况如下表所示:
甲组
84
85
87
88
88
90
乙组
82
86
87
88
89
90
(1)根据表中的数据,哪个组对精神文明建设知识的掌握更为稳定?
(2)用简单随机抽样方法从乙组6名成员中抽取两名,他们的得分情况组成一个样本,求抽出的两名成员的分数差值至少是4分的概率。
解析:(1)由题意可知,
, ………………1分
………………2分
……3分
……4分
因为,所以甲组的成绩比乙组稳定。 ………6分
(2)从乙组抽取两名成员的分数,所有基本事件为(用坐标表示):(82,86),(82,87),(82,87),(82,89),(82,90),(86,87),(86,88),(86,89),(86,90),(87,88)(87,89)(87,90),(88,89),(88,90),(89,90)共15种情况。 ………………8分
则抽取的两名成员的分数差值至少是4的事件包含:(82,86),(82,87),(82,87),(82,89),(82,90),(86,90)共6种情况。 ………………10分
由古典概型公式可知,抽取的两名成员的分数差值至少是4分的概率P=
8.某研究性学习小组对春季昼夜温差大小与某花卉种子发芽多少之间的关系进行研究,他们分别记录了3月1日至3月5日的每天昼夜温差与实验室每天每100颗种子浸泡后的发芽数,得到如下资料:
日期
3月1日
3月2日
3月3日
3月4日
3月5日
温差x(oC)
10
11
13
12
8
发芽数y(颗)
23
25
30
26
16
(I)从3月1日至3月5日中任选2天,记发芽的种子数分别为m,n,求事件“m,n均小于25”的概率;
(II)请根据3月2日至3月4日的数据,求出y关于x的线性回归方程;
(III)
若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(II)所得的线性回归方程是否可靠?
(参考公式:回归直线方程式,其中)
(I)m,n构成的基本事件(m,n)有:(23,25),(23,30),(23,26),(23,16),(25,30),(25,26),(25,16),(30,26),(30,16),(26,16),共有10个.
………………………………………………………………2分
其中“m,n均小于25”的有1个,其概率为. ………………………4分
(II)∵
∴. ………………………6分
于是,. ……………………………………………8分
故所求线性回归方程为. …………………………………………9分
(III)由(2)知,
当x=10时,y=22;当x=8时,y=17. ………………………………………11分
与检验数据的误差均为1,满足题意.
故认为得到的线性回归方程是可靠的.
9.在甲、乙两个盒子中分别装有标号为1、2、3、4的四个球,现从甲、乙两个盒子中各取出1个球,每个小球被取出的可能性相等。
(1)求取出的两个球上标号为相邻整数的概率;
(2)求取出的两个球上标号之和能被3整除的概率.
(Ⅰ)当时,~.--------------------------3分
故,. ---------6分
(Ⅱ)的可取值为.
;
;
--------------------10分
的分布列为
0
1
2
3
P
----------------------12分
10. 为了解学生喜欢数学是否与性别有关,对50个学生进行了问卷调查得到了如下的列联表:
喜欢数学
不喜欢数学
合计
男生
5
女生
10
合计
50
已知在全部50人中随机抽取1人抽到喜欢数学的学生的概率为.
(1)请将上面的列联表补充完整(不用写计算过程);
(2)是否有99.5%的把握认为喜欢数学与性别有关?说明你的理由;
下面的临界值表供参考:
0.15
0.10
0.05
0.025
0.010
0.005
0.001
2.072
2.706
3.841
5.024
6.635
7.879
10.828
(参考公式:,其中)
.解:解:(1) 列联表补充如下:
喜爱数学
不喜爱数学
合计
男生
20
5
25
女生
10
15
25
合计
30
20
50
------5分
(2)∵------------------------10分
∴有99.5%的把握认为喜爱数学与性别有关.---------------------12分
11.
O
60 65 70 75 80 85 疱疹面积
0.03
0.04
0.05
0.06
注射药物B后皮肤疱疹面积频率分布直方图
注射药物A后皮肤疱疹面积的频数分布表
疱疹面积
频数
20
50
20
10
为了比较注射两种药物后产生的皮肤疱疹的面积,选200只老鼠做试验,将这200只老鼠随机地分成两组,每组100只,其中一组注射药物(称为组),另一组注射药物(称为组),则两组老鼠皮肤疱疹面积(单位:)的频率分布表、频率分布直方图分别如下.
(Ⅰ)为方便两组试验对比,现都用分层抽样方法从
两组中各挑出20只老鼠,求两组成肤疱疹
面积同为的这一区间应分别挑出几只?
(Ⅱ)在(Ⅰ)的条件下,将两组挑出的皮肤疱疹面积
同为这一区间上的老鼠放在一起观察,几天
后,从中抽取两只抽血化验,求组中至少有1只被
抽中的概率.
【解】(Ⅰ)由组频数分布表可知,组中这一小组的频数为20,………1分
由组频率分布直方图可知,组中这一小组的频率为
…………………3分
所以这一小组频数为……………………4分
由于是分层抽样,所以,…………………5分
即两组中成肤疱疹面积同为的这一区间应分别挑出4只、2只………6分
(Ⅱ)由(Ⅰ)知,两组中这一区间上挑出的老鼠分别有4只、2只,
设编号分别为1,2,3,4;5(组),6(组), …………………7分
则从中抽取两只的所有基本事件如下
(1,2), (1,3), (1,4), (1,5), (1,6); (2,3), (2,4), (2,5),(2,6); (3,4), (3,5),(3,6); (4,5),(4,6); (5,6)
共有15个……………………………………8分
显然事件{组中至少有1只被抽中}发生包含了以下9个基本事件,
(1,5), (1,6); (2,5),(2,6); (3,5),(3,6); (4,5),(4,6); (5,6)……………10分
所以由古典概型知
12.已知集合在平面直角坐标系中,点M(x,y)的坐标。
(1)请列出点M的所有坐标;
(2)求点M不在x轴上的概率;
(3)求点M正好落在区域上的概率。
解:(1)集合A={-2,0,1,3},点M(x,y)的坐标,
点M的坐标共有:个,分别是:
(-2,-2),(-2,0),(-2,1),(-2,3);(0,-2),(0,0),(0,1),(0,3);
(1,-2),(1,0),(1,1),(1,3);(3,-2),(3,0),(3,1),(3,3)…………………….4分
(2)点M不在x轴上的坐标共有12种:
(-2,-2),(-2,0),(-2,1),(-2,3);(1,-2),(1,0),(1,1),(1,3);
(3,-2),(3,0),(3,1),(3,3)
所以点M不在x轴上的概率是………………………………………..8分
(3)点M正好落在区域上的坐标共有3种:(1,1),(1,3),(3,1)
故M正好落在该区域上的概率为
13.中华人民共和国道路交通安全法》规定:车辆驾驶员血液酒精浓度在20~80 mg/100 ml(不含80)之间,属于酒后贺车;在80 mg /100 ml (含80)以上时,属醉酒贺车,对于酒后驾车和醉酒驾车的驾驶员公安机关将给予不同程度的处罚.
某市公安局交通管理部门在某路段的一次拦查行动中,依法检查了250辆机动车,查出酒后驾车和醉酒贺车的驾驶员20人,下图是对这20人血液中酒精含量进行检查所得结果的频率分布直方图.
(1)根据频率分布直方图,求:此次抽查的250人中,醉酒驾车的人数;
(2)从血液酒精浓度在[70,90)范围内的驾驶员中任取2人,求恰有1人属于醉酒驾车的概率.
解: (1)
酒精含量(单位:mg/100ml)
[20,30)
[30,40)
[40,50)
[50,60)
人数
3
4
4
1
酒精含量(单位:mg/100ml)
[60,70)
[70,80)
[80,90)
[90,100]
人数
2
3
2
1
所以醉酒驾车的人数为人………………………………………………6分
(2)因为血液酒精浓度在[70,80)内范围内应抽3人,记为a,b,c, [80,90)范围内有2人,记为d,e,则从中任取2人的所有情况为(a,b),(a,c),(a,d),(a,e),(b,c),(b,d),(b,e),(c,d),(c,e),(d,e),共10种…………………………………………….8分
恰有一人的血液酒精浓度在[80,90)范围内的情况有(a,d),(a,e),(b,d),(b,e),(c,d),(c,e),共6种,……………………………………………………………………….10分
设“恰有1人属于醉酒驾车”为事件A,则P(A)==.……
14. 是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.我国标准采用世卫组织设定的最宽限值,日均值在35微克/立方米以下空气质量为一级;在35微克/立方米75微克/立方米之间空气质量为二级;在75微克/立方米及其以上空气质量为超标.
某试点城市环保局从该市市区2011年全年每天的监测数据中随机抽取6天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶),若从这6天的数据中随机抽出2天.
(Ⅰ)求恰有一天空气质量超标的概率;
(Ⅱ)求至多有一天空气质量超标的概率.
解: 由茎叶图知:6天有4天空气质量未超标,有2天空气质量超标. …………2分
记未超标的4天为,超标的两天为.则从6天中抽取2天的所有情况为:,,,,,,,,,,,,,,,基本事件数为15.…………4分
(Ⅰ)记 “6天中抽取2天,恰有1天空气质量超标”为事件,可能结果为:,,,,,,,,基本事件数为.
∴;……………6分
(Ⅱ)记“至多有一天空气质量超标”为事件,
“2天都超标”为事件,其可能结果为,…………………………8分
故,…………………………………………………………10分
∴.
15.为加强中学生实践、创新能力和团队精神的培养,促进教育教学改革,郑州市教育局举办了全市中学生创新知识竞赛.某校举行选拔赛,共有200名学生参加,为了解成绩情况,从中抽取50名学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成的频率分布表,解答下列问题:
(I)若用系统抽样的方法抽取50个样本,现将所有学生随机地编号为000,001,002,…,199,试写出第二组第一位学生的编号;
(II) 求出a,b,c,d,e的值(直接写出结果),并作出频率分布直方图;
(III)若成绩在85.5〜95. 5分的学生为二等奖,问参赛学生中获得二等奖的学生约为多少人?
[解析] (Ⅰ)编号为004. ……3分
(Ⅱ) a,b,c,d,e的值分别为
13, 4, 0.30, 0.08, 1.…… ……8分
(Ⅲ)在被抽到的学生中获二等奖的人数
9+2=11(人),占样本的比例是=0.22,
即获二等奖的概率为22%,所以获二等奖
的人数估计为200×22%=44(人).
答:获二等奖的大约有44人.……12分
16.某日用品按行业质量标准分成五个等级,等级系数X依次为1,2,3,4,5.现从一批该日用品中随机抽取20件,对其等级系数进行统计分析,得到频率分布表如下:
X
1
2
3
4
5
频率
a
0.2
0.4
b
c
(I)若所抽取的20件日用品中,等级系数为4的恰有3件,等级系数为5的恰有2件,求a,b,c的值;
(Ⅱ)在(I)的条件下,将等级系数为4的3件日用品记为x1,x2,x3,等级系数为5的2件日用品记为y1,y2,现从x1,x2,x3,y1,y2这5件日用品中任取两件(假定每件日用品被取出的可能性相同),写出所有可能的结果,并求这两件日用品的等级系数恰好相等的概率.
解:(Ⅰ)由频率分布表得a+0.2+0.45+b+c=1,即a+b+c=0.35.
因为抽取的20件日用品中,等级系数为4的恰有3件,所以b==0.15.
等级系数为5的恰有2件,所以c==0.1.
从而a=0.35-b-c=0.1.
所以a=0.1,b=0.15,c=0.1. ………………6分
(Ⅱ)从日用品x1,x2,x3,y1,y2中任取两件,所有可能的结果为:
{x1,x2},{x1,x3},{x1,y1},{x1,y2},{x2,x3},{x2,y1},{x2,y2},{x3,y1},{x3,y2},{y1,y2}.
设事件A表示“从日用品x1,x2,x3,y1,y2中任取两件,其等级系数相等”,则A包含的基本事件为:
{x1,x2},{x1,x3},{x2,x3},{y1,y2},共4个.
又基本事件的总数为10,
故所求的概率P(A)==0.4.
17. 已知A、B、C三个箱子中各装有2个完全相同的球,每个箱子里的球,有一个球标着号码1,另一个球标着号码2,现从A、B、C三个箱子中各摸出1个球。
(1)若用数组(x,y,z)中的x、y、z分别表示从A、B、C三个箱子中摸出的球的号码,请写出数组(x,y,z)的所有情形,并回答一共有多少种;
(2)如果请您猜测摸出的这三个球的号码之和,猜中有奖,那么猜什么数获奖的可能性最大?请说明理由。
(1)解:数组(x,y,z)的所有情形为:(1,1,1),(1,1,2),(1,2,1),(1,2,2),(2,1,1),(2,1,2),(2,2,1),(2,2,2),共8种 6分
注:列出所有情形,得6分,列出5种以上情形,得4分.
(2)解:摸出的三个球号码的和可能为3,4,5,6,故记“所摸出的三个球号码之和为i”为事件Ai (i = 3,4,5,6) 8分
易知,事件A3包含有1个基本事件,事件A4包含有3个基本事件,事件A5包含有3个基本事件,事件A6包含有1个基本事件 10分
∴
18.有关部门要了解甲型H1N1流感预防知识在学校的普及情况,命制了一份有道题的问卷到各学校做问卷调查.某中学两个班各被随机抽取名学生接受问卷调查,班名学生得分为:,,,,;班5名学生得分为:,,,,.
(Ⅰ)请你估计两个班中哪个班的问卷得分要稳定一些;
(Ⅱ)如果把班名学生的得分看成一个总体,并用简单随机抽样方法从中抽取样本容量为的样本,求样本平均数与总体平均数之差的绝对值不小于的概率.
解:(Ⅰ)∵班的名学生的平均得分为÷, ………1分
方差;……3分
班的名学生的平均得分为÷, ……………………4分
方差. ……6分
∴ ,
∴ 班的预防知识的问卷得分要稳定一些. …………………………8分
(Ⅱ)从班名同学中任选名同学的方法共有种, …………………10分
其中样本和,和,和,和的平均数满足条件,故所求概率为.
19.
近年来,我国机动车拥有量呈现快速增加的趋势,可与之配套的基础设施建设速度相对迟缓,交通拥堵问题已经成为制约城市发展的重要因素,为了解某市的交通状况,现对其6条道路进行评估,得分分别为5、6、7、8、9、10规定评估的平均得分与全市的总体交通状况等级如下表:
评估的平均得分
[0,6]
[6,8]
[8,10]
全市的总体交通
不合格
合格
优秀
(1)求本次评估的平均得分,并参照上表估计该市的总体交通状况等级。
(2)用简单随机抽样方法从6条道路中抽取2条,它们的得分组成一个样本,求该样本的平均数与总体的平均数之差的绝对值不超过0.5的概率。
解:(1)合格---------------------6分
(2)基本事件为(5,6)(5,7)(5,8)(5,9)(5,10)(6,7)(6,8)(6,9)(6,10)(7,8)(7,9)(7,10) (8,9)(8,10)(9,10)共15个
19.(本小题满分12分)
一工厂生产甲, 乙, 丙三种样式的杯子,每种样式均有500ml和700ml两种型号,
某天的产量如右表(单位:个):
型号
甲样式
乙样式
丙样式
500ml
2000
z
3000
700ml
3000
4500
5000
按样式进行分层抽样,在该天生产的杯子中抽取100个,其中有甲样式杯子25个.
(I)求z的值;
(II)用分层抽样的方法在甲样式杯子中抽取一个容量为5的样本,从这个样本中任取2个杯子,求至少有1个500ml杯子的概率.
解: (I)设该厂本月生产的乙样式的杯子为n个,在丙样式的杯子中抽取x个,由题意得, ,所以x=40. -----------2分
则100-40-25=35,所以,n=7000,
故z=2500 ----------6分
(II)设所抽样本中有m个500ml杯子,
因为用分层抽样的方法在甲样式杯子中抽取一个容量为5的样本,
所以,解得m=2 -----------9分
也就是抽取了2个500ml杯子,3个700ml杯子,分别记作S1,S2;B1,B2,B3,则从中任取2个的所有基本事件为(S1, B1), (S1, B2) , (S1, B3) (S2 ,B1), (S2 ,B2), (S2 ,B3),( (S1, S2),(B1 ,B2), (B2 ,B3) ,(B1 ,B3)共10个,其中至少有1个500ml杯子的基本事件有7个基本事件:
(S1, B1), (S1, B2) , (S1, B3) (S2 ,B1), (S2 ,B2), (S2 ,B3),( (S1, S2),所以从中任取2个,
至少有1个500ml杯子的概率为.
20.一化工厂因排污趋向严重,2011年1月决定着手整治。经调研,该厂第一个月的污染度为,整治后前四个月的污染度如下表;
月数
1
2
3
4
……
污染度
60
31
13
0
……
污染度为后,该工厂即停止整治,污染度又开始上升,现用下列三个函数模拟从整治后第一个月开始工厂的污染模式:
,,,其中表示月数,分别表示污染度.
(参考数据:)
(Ⅰ)问选用哪个函数模拟比较合理,并说明理由;
(Ⅱ)如果环保部门要求该厂每月的排污度均不能超过60,若以比较合理的模拟函数预测,该厂最晚在何时开始进行再次整治?
(Ⅰ) …………3分
…………6分
由此可得更接近实际值,所以用模拟比较合理. …………7分
(Ⅱ)因在上是增函数,又因为 ………12分
这说明第一次整治后有16个月的污染度不超过60,
故应在2012年5月起开始再次整治.
21. 某校高三年级共有450名学生参加英语口语测试,其中男生250名,女生200名。现按性别用分层抽样的方法从中抽取45名学生的成绩。
(I)求抽取的男生与女生的人数?
(II)从男生和女生中抽查的结果分别如下表1和表2;
表1
成绩分组
人数
3
m
8
6
表2
成绩分组
人数
2
5
n
5
分别估计男生和女生的平均分数,并估计这450名学生的平均分数。(精确到0.01)
解析:(Ⅰ)由抽样方法知,被抽取的男生人数为250×=25,
被抽取的女生人数为200×=20.……………………………………………2分
(Ⅱ)男生甲和女生乙被抽到的概率均为0.1,所以男生甲与女生乙至少有1人被抽到的概率:P=1-(1-0.1)2=0.19.……………………………………………………………7分
(Ⅲ)由(Ⅰ)知,m=25-(3+8+6)=8,n=20-(2+5+5)=8,据此估计
男生平均分为=81.8,
女生平均分为=83;
这450名学生的平均分数为≈82.33.
22. 设平顶向量= ( m , 1), = ( 2 , n ),其中 m, n {1,2,3,4}.
(I)请列出有序数组( m,n )的所有可能结果;
(II)记“使得(-)成立的( m,n )”为事件A,求事件A发生的概率。
(II)由得,即。由于,故事件A包含的基本事件为(2,1)和(3,4),共2个。又基本事件的总数为16,故所求的概率为。……………………12
23.某校高一某班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下,据此解答如下问题:
(1)求分数在[50,60)的频率及全班人数;
(2)求分数在[80,90)之间的频数,并计算频率分布直方图中[80,90)间的矩形的高;
(3)若要从分数在[80,100]之间的试卷中任取两份分析学生失分情况,在抽取的试卷中,求至少有一份分数在[90,100]之间的概率.
解:(1)分数在[50,60)的频率为0.008×10=0.08,(2分)
由茎叶图知:分数在[50,60)之间的频数为2,所以全班人数为=25,(4分)
(2)分数在[80,90)之间的频数为25-2-7-10-2=4;(6分)
频率分布直方图中[80,90)间的矩形的高为÷10=0.016.(8分)
(3)将[80,90)之间的4个分数编号为1,2,3,4,[90,100]之间的2个分数编号为5,6,
在[80,100]之间的试卷中任取两份的基本事件为:
(1,2),(1,3),(1,4),(1,5),(1,6),
(2,3),(2,4),(2,5),(2,6),
(3,4),(3,5),(3,6),
(4,5),(4,6),
(5,6)共15个,(10分)
其中,至少有一个在[90,100]之间的基本事件有9个,
故至少有一份分数在[90,100]之间的概率是=0.6.(12分)
24.甲乙二人用4张扑克牌(分别是红桃2, 红桃3, 红桃4, 方片4)玩游戏,他们将扑克牌洗匀后,背面朝上放在桌面上,甲先抽,乙后抽,抽出的牌不放回,各抽一张.
(1)设分别表示甲、乙抽到的牌,写出甲乙二人抽到的牌的所有情况.
(2)若甲 抽到红桃3,则乙抽出的牌的牌面数字比3大的概率是多少?
(3)甲乙约定:若甲抽到的牌面数字比乙大,则甲胜,反之,则乙胜。你认为此游戏是否公平,说明你的理由。
26. 某车间在两天内,每天生产10件某产品,其中第一天、第二天分别生产出了1件、2件次品.而质检部门每天要从生产的10件产品中随意抽取4件进行检查,若发现有次品,则当天的产品不能通过.
(Ⅰ)求第一天产品通过检查的概率;
(Ⅱ)(文)求两天全部通过的概率.
(解:(Ⅰ)∵随意抽取4件产品检查是随机事件,而第一天有9件正品.
∴第一天通过检查的概率为. ……………………………4分
(Ⅱ)同(Ⅰ),第二天通过检查的概率为. …………………9分
因第一、第二天是否通过检查相互独立, ……………………………10分
所以,两天全部通过检查的概率为. …………12分
27.某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究,他们分别记录了12月1日至12月5日的每天昼夜温差与实验室每天每100颗种子中的发芽数,得到如下资料:
日 期
12月1日
12月2日
12月3日
12月4日
12月5日
温差x(°C)
10
11
13
12
8
发芽数y(颗)
23
25
30
26
16
该农科所确定的研究方案是:先从这五组数据中选取2组,用剩下的3组数据求线性回归方程,再对被选取的2组数据进行检验.
(1)求选取的2组数据恰好是不相邻2天数据的概率;
(2)若选取的是12月1日与12月5日的两组数据,请根据12月2日至12月4日的数据,求出y关于x的线性回归方程;并预报当温差为9 0C时的种子发芽数。
解:(1)设抽到不相邻的两组数据为事件A,从5组数据中选取2组数
据共有10种情况:(1,2)(1,3)(1,4)(1,5)(2,3)
(2,4)(2,5)(3,4)(3,5)(4,5),
····················3分
其中数据为12月份的日期数.每种情况都是可能出现的,
事件A包括的基本事件有6种.
∴P(A)=
∴选取的2组数据恰好是不相邻2天数据的概率是
····················6分
(2)由数据,求得 .
····················8分
由公式,求得b=
∴y关于x的线性回归方程为x-3.
····················10分
由此可以预报当温差为9 0C时的种子发芽数为19或20颗
····················12分
28.现从3道选择题和2道填空题中任选2题.
(Ⅰ)求选出的2题都是选择题的概率;(Ⅱ)求选出的两题中至少1题是选择题的概率.
解(Ⅰ)记“选出两道都是选择题”为A,5题任选2题,共有种,
其中,都是选择题有3种.……………2分 ∴ .………………………4分
(Ⅱ).记“选出1道选择题,1道填空题”为B,
∴ ……………………………10分
所以,至少有1道选择题的概率 ……………12分
29.先后随机投掷2枚正方体骰子,其中表示第枚骰子出现的点数,表示第枚骰子出现的点数. (Ⅰ)求点在直线上的概率; (Ⅱ)求点满足的概率.
解:(Ⅰ)每颗骰子出现的点数都有种情况,
所以基本事件总数为个. …………………… 2分
记“点在直线上”为事件,有5个基本事件:
, …………………… 5分
…………………… 6分
(Ⅱ)记“点满足”为事件,则事件有个基本事件:
当时,当时,; …………………… 7分
当时,;当时, …………………… 9分
当时,;当时,. 11分 12分
30.有两个不透明的箱子,每个箱子都装有4个完全相同的小球,球上分别标有数字1、2、3、4.
(Ⅰ)甲从其中一个箱子中摸出一个球,乙从另一个箱子摸出一个球,谁摸出的球上标的数字大谁就获胜(若数字相同则为平局),求甲获胜的概率;(Ⅱ)摸球方法与(Ⅰ)同,若规定:两人摸到的球上所标数字相同甲获胜,所标数字不相同则乙获胜,这样规定公平吗?
解:(Ⅰ)用(表示甲摸到的数字,表示乙摸到的数字)表示甲、乙各摸一球构成的基本事件,则基本事件有:、、、、、、、、、、、、、、、
,共16个; -------------------3分
设:甲获胜的的事件为A,则事件A包含的基本事件有:、、、、、,共有6个;则 ------------------------------5分 ------------------------------6分
(Ⅱ)设:甲获胜的的事件为B,乙获胜的的事件为C;事件B所包含的基本事件有:、、、,共有4个;则 -------------------------8分
----------------------10分
,所以这样规定不公平. -----------------11分
答:(Ⅰ)甲获胜的概率为;(Ⅱ)这样规定不公平. -----------------------12分
本资料由《七彩教育网》www.7caiedu.cn 提供!
本资料来源于《七彩教育网》http://www.7caiedu.cn