高考数学 立体几何大题30题 30页

立体几何大题 1．如下图，一个等腰直角三角形的硬纸片 ABC 中，∠ACB＝90°，AC＝4cm，CD 是斜边 上的高沿 CD 把△ABC 折成直二面角． （1）如果你手中只有一把能度量长度的直尺，应该如何确定 A，B 的位置，使二面角 A－CD－B 是直二面角？证明你的结论． （2）试在平面 ABC 上确定一个 P，使 DP 与平面 ABC 内任意一条直线都垂直，证明 你的结论． （3）如果在折成的三棱锥内有一个小球，求出小球半径的最大值． 解：（1）用直尺度量折后的 AB 长，若 AB＝4cm，则二面角 A－CD－B 为直二面角． ∵ △ABC 是等腰直角三角形，  ,cm22DBAD  又∵ AD⊥DC，BD⊥DC． ∴ ∠ADC 是二面角 A－CD－B 的平面角． 有时当 ,cm4AB,22DBAD   .90ADB.ABDBAD 222  （2）取△ABC 的中心 P，连 DP，则 DP 满足条件 ∵ △ABC 为正三角形，且 AD＝BD＝CD． ∴ 三棱锥 D－ABC 是正三棱锥，由 P 为△ABC 的中心，知 DP⊥平面 ABC， ∴ DP 与平面内任意一条直线都垂直． （3）当小球半径最大时，此小球与三棱锥的 4 个面都相切，设小球球心为 0，半径为 r， 连结 OA，OB，OC，OD，三棱锥被分为 4 个小三棱锥，且每个小三棱锥中有一个面上的高 都为 r，故有 ABCOABDOADCOBCDOBCDA VVVVV   代入得 3 623r   ，即半径 最大的小球半径为 3 623  ． A B C 第1题图 A B C D 第1题图 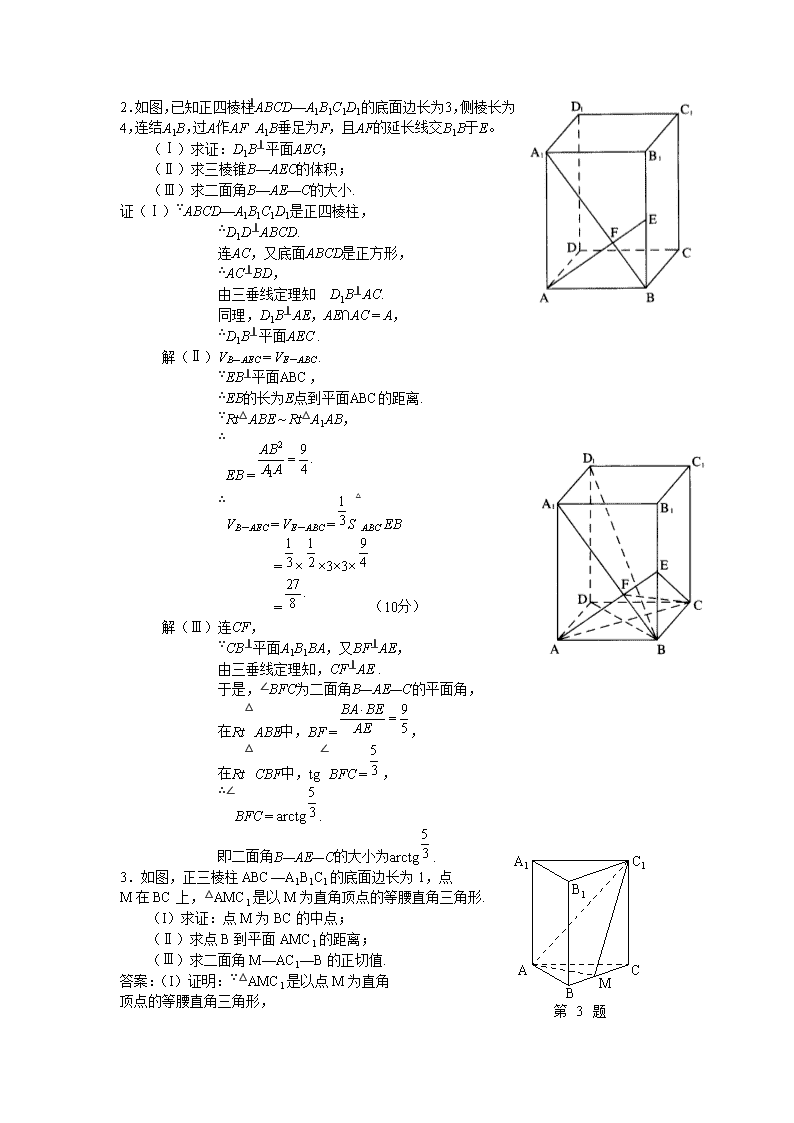2．如图，已知正四棱柱ABCD—A1B1C1D1的底面边长为3，侧棱长 为4，连结A1B，过A作AF⊥A1B垂足为F，且AF的延长线交B1B于E。 （Ⅰ）求证：D1B⊥平面AEC； （Ⅱ）求三棱锥B—AEC的体积； （Ⅲ）求二面角B—AE—C的大小. 证（Ⅰ）∵ABCD—A1B1C1D1是正四棱柱， ∴D1D⊥ABCD. 连AC，又底面ABCD是正方形， ∴AC⊥BD， 由三垂线定理知 D1B⊥AC. 同理，D1B⊥AE，AE∩AC = A， ∴D1B⊥平面AEC . 解（Ⅱ）VB－AEC = VE－ABC . ∵EB⊥平面ABC， ∴EB的长为E点到平面ABC的距离. ∵Rt△ABE ~ Rt△A1AB， ∴EB = . 4 9 1 2  AA AB ∴VB－AEC = VE－ABC = 3 1 S△ABC·EB = 3 1 × 2 1 ×3×3× 4 9 = . 8 27 （10分） 解（Ⅲ）连CF， ∵CB⊥平面A1B1BA，又BF⊥AE， 由三垂线定理知，CF⊥AE . 于是，∠BFC为二面角B—AE—C的平面角， 在Rt△ABE中，BF = 5 9   AE BEBA ， 在Rt△CBF中，tg∠BFC = 3 5 ， ∴∠BFC = arctg 3 5 . 即二面角B—AE—C的大小为arctg 3 5 . 3．如图，正三棱柱 ABC—A1B1C1的底面边长为 1，点 M 在 BC 上，△AMC1 是以 M 为直角顶点的等腰直角三角形. （I）求证：点 M 为 BC 的中点； （Ⅱ）求点 B 到平面 AMC1 的距离； （Ⅲ）求二面角 M—AC1—B 的正切值. 答案：（I）证明：∵△AMC1是以点 M 为直角 顶点的等腰直角三角形， A B C A1 B1 C1 M 第3题图 ∴AM⊥MC1 且 AM=MC1 ∵在正三棱柱 ABC—A1B1C1中， 有 CC1⊥底面 ABC. ∴C1M 在底面内的射影为 CM， 由三垂线逆定理，得 AM⊥CM. ∵底面 ABC 是边长为 1 的正三角形， ∴点 M 为 BC 中点. （II）解法（一） 过点 B 作 BH⊥C1M 交其延长线于 H. 由（I）知 AM⊥C1M，AM⊥CB， ∴AM⊥平面 C1CBB1. ∴AM⊥BH. ∴BH⊥平面 AMC1. ∴BH 为点 B 到平面 AMC1的距离. ∵△BHM∽△C1CM. AM=C1M= , 2 3 在 Rt△CC1M 中，可求出 CC1 . 2 2 . 6 6 2 3 2 1 2 211  BHBH MC BM CC BH 解法（二） 设点 B 到平面 AMC1的距离为 h. 则 11 BMCAAMCB VV   由（I）知 AM⊥C1M，AM⊥CB， ∴AM⊥平面 C1CBB1 ∵AB=1，BM= . 2 2, 2 3, 2 1 11  CCMCAM可求出 AMShS MBCAMC   11 3 1 3 1 2 3 2 2 2 1 2 1 3 1 2 3 2 3 2 1 3 1  h 6 6 h （III）过点 B 作 BI⊥AC1于 I，连结 HI. ∵BH⊥平面 C1AM，HI 为 BI 在平面 C1AM 内的射影. ∴HI⊥AC1，∠BIH 为二面角 M—AC1—B 的平面角. 在 Rt△BHM 中， , 2 1, 6 6  BMBH ∵△AMC1为等腰直角三角形，∠AC1M=45°. ∴△C1IH 也是等腰直角三角形. 由 C1M= . 3 32, 6 3, 2 3 1 22  HCBHBMHM 有 ∴ . 3 6 HI . 2 1  HI BHBIHtg 4．如图，已知多面体 ABCDE 中，AB⊥平面 ACD，DE⊥平面 ACD，三角形 ACD 是正三 角形，且 AD=DE=2，AB=1，F 是 CD 的中点． （Ⅰ）求证：AF∥平面 BCE； （Ⅱ）求多面体 ABCDE 的体积； （Ⅲ）求二面角 C-BE-D 的正切值． 证：（Ⅰ）取 CE 中点 M，连结 FM，BM，则有 ABDEFM // 2 1// ． ∴四边形 AFMB 是平行四边形． ∴AF//BM， ∵ BM 平面 BCE， AF 平面 BCE， ∴AF//平面 BCE． （Ⅱ）由于 DE⊥平面 ACD， 则 DE⊥AF． 又△ACD 是等边三角形，则 AF⊥CD．而 CD∩DE=D，因此 AF⊥平面 CDE． 又 BM//AF，则 BM⊥平面 CDE． BMABVVV CDEBACDBABCDE   22 2 1 3 12 4 3 3 1 2 32 2 3 3 2 3 3  ． （Ⅲ）设 G 为 AD 中点，连结 CG，则 CG⊥AD． 由 DE⊥平面 ACD， CG 平面 ACD， 则 DE⊥CG，又 AD∩DE=D， ∴CG⊥平面 ADEB． 作 GH⊥BE 于 H，连结 CH，则 CH⊥BE． ∴∠CHG 为二面角 C-BE-D 的平面角． 由已知 AB=1，DE=AD=2，则 3CG ， ∴ 2 312 2 111 2 12)21( 2 1 GBES ． 不难算出 5BE ． ∴ 2 35 2 1  GHS GBE ，∴ 5 3 GH ． ∴ 3 15  GH CGCHGtg ． 5．已知：ABCD 是矩形，设 PA=a，PA⊥平面 ABCD.M、N 分别是 AB、PC 的中点. （Ⅰ）求证：MN⊥AB； （Ⅱ）若 PD=AB，且平面 MND⊥平面 PCD，求二面角 P—CD—A 的大小； （Ⅲ）在（Ⅱ）的条件下，求三棱锥 D—AMN 的体积. （Ⅰ）连结 AC，AN. 由 BC⊥AB，AB 是 PB 在 底面 ABCD 上的射影. 则有 BC⊥PB. 又 BN 是 Rt△PBC 斜边 PC 的中线， 即 PCBN 2 1  . 由 PA⊥底面 ABCD，有 PA⊥AC， 则 AN 是 Rt△PAC 斜边 PC 的中线， 即 PCAN 2 1  BNAN  又∵M 是 AB 的中点， ABMN  （也可由三垂线定理证明） （Ⅱ）由 PA⊥平面 ABCD，AD⊥DC，有 PD⊥DC. 则∠PDA 为平面 PCD 与平面 ABCD 所成二面角的平面角 由 PA=a，设 AD=BC=b，CD=AB=c， 又由 AB=PD=DC，N 是 PC 中点， 则有 DN⊥PC 又∵平面 MND⊥平面 PCD 于 ND， ∴PC⊥平面 MND ∴PC⊥MN， 而 N 是 PC 中点，则必有 PM=MC. bacbca  . 4 1 4 1 2222 此时 4 ,1   PDAPDAtg . 即二面角 P—CD—A 的大小为 4  （Ⅲ） AMDNAMND VV   ，连结 BD 交 AC 于 O，连结 NO，则 NO 2 1 PA. 且 NO⊥ 平面 AMD，由 PA=a 3 24 2 3 1 aNOSV AMDAMDN   . 6．如图，正方体 ABCD—A1B1C1D1中，P、M、N 分别为棱 DD1、AB、BC 的中点。 （I）求二面角 B1—MN—B 的正切值； （II）证明：PB⊥平面 MNB1； （III）画出一个正方体表面展开图，使其满足 “有 4 个正方形面相连成一个长方形”的条件， ∥ ＝ A B CD P A1 B1 C1 D1 第6题图 M N 并求出展开图中 P、B 两点间的距离。 解：（I）连接 BD 交 MN 于 F，则 BF⊥MN， 连接 B1F ∵B1B⊥平面 ABCD ∴B1F⊥MN 2 分 则∠B1FB 为二面角 B1—MN—B 的平面角 在 Rt△B1FB 中，设 B1B=1，则 FB  2 4 ∴ tg B FB∠ 1 2 2 4 分 （II）过点 P 作 PE⊥AA1，则 PE∥DA，连接 BE 又 DA⊥平面 ABB1A1，∴PE⊥平面 ABB1A1 又 BE⊥B1M ∴PB⊥MB1 又 MN∥AC，BD⊥AC，∴BD⊥MN 又 PD⊥平面 ABCD ∴PB⊥MN，所以 PB⊥平面 MNB1 11 分 （III） PB  13 2 ，符合条件的正方体表面展开图可以是以下 6 种之一： 7．如图，四棱锥 P—ABCD 的底面是正方形,PA⊥底面 ABCD，PA=AD=2，点 M、N 分别在棱 PD、PC 上，且 PC⊥平面 AMN. （Ⅰ）求证：AM⊥PD； （Ⅱ）求二面角 P—AM—N 的大小； （Ⅲ）求直线 CD 与平面 AMN 所成角的大小. （I）证明：∵ABCD 是正方形，∴CD⊥AD， ∵PA⊥底面 ABCD，∴PA⊥CD. ∴CD⊥平面 PAD ∵AM平面 PAD，∴CD⊥AM. ∵PC⊥平面 AMN，∴PC⊥AM. ∴AM⊥平面 PCD. ∴AM⊥PD （II）解：∵AM⊥平面 PCD（已证）. ∴AM⊥PM，AM⊥NM. ∴∠PMN 为二面角 P-AM-N 的平面角 ∵PN⊥平面 AMN，∴PN⊥NM. 在直角△PCD 中，CD=2，PD=2 2 ，∴PC=2 3 . ∵PA=AD，AM⊥PD，∴M 为 PD 的中点， PM= 2 1 PD= 2 由 Rt△PMN∽Rt△PCD，得 ∴ PC PMCDMN   . . 3 3arccos. 3 3 32 2)cos(  PMN PC CD PM MNPMN 即二面角 P—AM—N 的大小为 3 3arccos . （III）解：延长 NM，CD 交于点 E. ∵PC⊥平面 AMN，∴NE 为 CE 在平面 AMN 内的射影 ∴∠CEN 为 CD（即（CE）与平在 AMN 所成的角 ∵CD⊥PD，EN⊥PN，∴∠CEN=∠MPN. 在 Rt△PMN 中， . 3 3arcsin) 2 ,0( . 3 3)sin(   MPNMPN PM MNMPN  ∴CD 与平面 AMN 所成的角的大小为 3 3arcsin 8．如图，在直三棱柱 ABC—A1B1C1 中，∠ACB=90°. BC=CC1=a，AC=2a. （I）求证：AB1⊥BC1； （II）求二面角 B—AB1—C 的大小； （III）求点 A1 到平面 AB1C 的距离. （1）证明：∵ABC—A1B1C1 是直三棱柱， ∴CC1⊥平面 ABC， ∴AC⊥CC1. ∵AC⊥BC， ∴AC⊥平面 B1BCC1. ∴B1C 是 AB1 在平面 B1BCC1上的射影. ∵BC=CC1， ∴四边形 B1BCC1 是正方形， ∴BC1⊥B1C. 根据三垂线定理得， AB1⊥BC1 （2）解：设 BC1∩B1C=O，作 OP⊥AB1于点 P， 连结 BP.∵BO⊥AC，且 BO⊥B1 C， ∴BO⊥平面 AB1C. ∴OP 是 BP 在平面 AB1C 上的射影. 根据三垂线定理得，AB1⊥BP. ∴∠OPB 是二面角 B—AB1—C 的平面角 ∵△OPB1~△ACB1， ∴ , 1 1 AB OB AC OP  ∴ . 3 3 1 1 a AB ACOBOP    在 Rt△POB 中， 2 6  OP OBOPBtg ， ∴二面角 B—AB1—C 的大小为 . 2 6arctg （3）解：[解法 1] ∵A1C1//AC，A1C1平 面 AB1C，∴A1C1//平面 AB1C. ∴点 A1 到 平面 AB1C 的距离与点 C1 到平面 AB1C.的 距离相等.∵BC1⊥平面 AB1C， ∴线段 C1O 的长度为点 A1到平面 AB1C 的 距离. ∴点 A1 到平面 AB1C 的距离为 . 2 2 1 aOC  [解法 2]连结 A1C，有 CAABCABA VV 1111   ，设点 A1到平面 AB1C 的距离为 h. ∵B1C1⊥平面 ACC1A1， ∴ 1111 CBShS ACAACB   ， 又 2 1 2 1 2 1,2 2 1 11 aAAACSaCBACS ACAACB   ， ∴ . 2 2 2 2 2 a a aah    ∴点 A1到平面 AB1C 的距离为 . 2 2 a 9．在长方体 ABCD－A1B1C1D1 中，已知 AB=BC=2，BB1=3，连接 BC1，过 B1 作 B1E⊥BC1 交 CC1于点 E (Ⅰ)求证：AC1⊥平面 B1D1E； (Ⅱ)求三棱锥 C1－B1D1E1的体积； (Ⅲ)求二面角 E－B1D1－C1的平面角大小 (1)证明：连接 A1C1 交 B1D1 于点 O ∵ABCD－A1B1C1D1 是长方体 ∴AA1⊥平面 A1B1C1D1，A1C1 是 AC1在平面 A1B1C1D1上的射影 ∵AB=BC，∴A1C1⊥B1D1， 根据三垂线定理得：AC1⊥B1D1； ∵AB⊥平面 BCC1B1，且 BC1⊥B1E， ∴AC1⊥B1E ∵B1D1∩B1E=B1， ∴AC1⊥平面 B1D1E1 (2)解：在 RT△BB1C1中， 1 1 1 1 1 3tg 2 B B BC B BC    在 RT△EC1B1中，C1E=B1C1·tg∠C1B1E=B1C1·ctg∠BC1B1=2 2 4 3 3  ， ∴VC1－B1D1E= VD1－B1C1E = 1 1 1 1 1 1 1 1 1 1 1 1 8( ) 3 3 2 9B C ES C D BC C E C D      (3)解：连接 OE，∵△B1C1E1≌△D1C1E1 ， ∴B1E=D1E ∵O是 B1D1中点， ∴B1D1⊥OE， ∴∠C1OE是二面角 E―B1D1―C1 的平面角 在 RT△OC1E中，∵ 1 1 1 2 2tg 3 C E C OE OC    所以，二面角 E―B1D1―C1的平面角为 2 2arctg 3 ， 10．在矩形 ABCD 中，AB＝4，BC＝3，E 为 DC 的中点，沿 AE 将△AED 折起，使二面角 D－AE－B 为 60 ． （Ⅰ）求 DE 与平面 AC 所成角的大小； （Ⅱ）求二面角 D－EC－B 的大小． 答案：如图 1，过点 D 作 DM⊥AE 于 M，延长 DM 与 BC 交于 N，在翻折过程中 DM⊥AE， MN⊥AE 保持不变，翻折后，如图 2，∠DMN 为二面角 D－AE－B 的平面角，∠DMN＝ 60 ，AE⊥平面 DMN，又因为 AE平面 AC，则 AC⊥平面 DMN． （Ⅰ）在平面 DMN 内，作 DO⊥MN 于 O， ∵平面 AC⊥平面 DMN， ∴DO⊥平面 AC． 连结 OE，DO⊥OE，∠DEO 为 DE 与平面 AC 所成的角． A D B CE A B C E D 第 10 题 图 如图 1，在直角三角形 ADE 中，AD＝3，DE＝2， ,1323DEADAE 2222  . 13 4 AE DEME, 13 6 AE DEADDM 2    如图 2，在直角三角形 DOM 中， , 13 3360sinDMDO  在直角三角形 DOE 中， 132 33 DE DODEOsin  ，则 . 26 393arcsinDEO  ∴DE 与平面 AC 所成的角为 . 26 393arcsin （Ⅱ）如图 2，在平面 AC 内，作 OF⊥EC 于 F，连结 DF， ∵DO⊥平面 AC，∴DF⊥EC，∴∠DFO 为二面角 D－EC－B 的平面角． 如图 1，作 OF⊥DC 于 F，则 Rt△EMD∽Rt△OFD， , DE EM DO OF  ∴ . DE EMDOOF   如图 2，在 Rt△DOM 中，OM＝DMcos∠DMO＝DM·cos60 ＝ 13 3 ． 如图 1， . 13 18OF, 13 9MODMDO  在 Rt△DFO 中， , 2 13 OF DODFOtg  ∴二面角 D－EC－B 的大小为 2 13arctg ． 11．直三棱柱 ABC－A1B1C1 中，AC＝CB＝AA1＝2，∠ACB＝90°，E 是 BB1的中点， D∈AB，∠A1DE＝90°. （Ⅰ）求证：CD⊥平面 ABB1A1； （Ⅱ）求二面角 D－A1C－A 的大小. 分平面 ，平面平面 ，平面，平面知，平面－由直三棱柱 ， 分的中点是），，（，即，有①、②由 ②，又 ①，）（，∥ ），，（，），，（ ），，（），，（则 分，），，（，可设，），，（，），，（又 ），，（，），，（则 坐标系如图，为原点，建立空间直角以 2. . 2..0111 .1090 20222 02202 2212 20020002 .120202 11 11 11111 11 1 1               AABBCD ABAABBABC ABCCDAABBABCCBAABC ABCDCBAC ABDDnm mnEDDADEA nmnmABAD ABnmAD nmDAnmED nmDABDBA EA C   （Ⅱ）解： 分的大小为－－二面角 ＞，＜ 分），，（的法向量，故可取平面平面显然 ），，（可取，可得令 ， 即 ，且则有 ，），，（的法向量为设平面 ），，（，），，（ 3. 3 3arccos . 3 3 13 1 |||| cos 4.010 .111.11 .0 .022 0 00 .202011 1 21 21 21 211 1 111 11 1                         ACAD nn nn nn nCAACAACB nzyx zx zx yx CAnCDn zyxnCDA CACD 12．如图，已知斜三棱柱 ABC—A1B1C1 中，∠BCA=90°，AC=BC=a，点 A1 在底面 ABC 上 的射影 恰为 AC 的中点 D，BA1⊥AC1。 （I）求证：BC⊥平面 A1ACC1； （II）求点 A1 到 AB 的距离 （III）求二面角 B—AA1—C 的正切值 解： 答案：如图，已知斜三棱柱 ABC—A1B1C1 中，∠BCA=90°，AC=BC=a，点 A1 在底面 ABC 上的射影 恰为 AC 的中点 D，BA1⊥AC1。 （I）求证：BC⊥平面 A1ACC1； （II）求点 A1到 AB 的距离 （III）求二面角 B—AA1—C 的正切值 解：（1）由题意，A1D⊥平面 ABC，∴A1D⊥BC。 又 AC⊥BC，∴BC⊥平面 A1ACC1 （II）过 D 作 DH⊥AB 于 H，又 A1D⊥平面 ABC，∴AB⊥A1H ∴A1H 是 H1 到 AB 的距离 ∵BA1⊥AC1，BC⊥平面 A1ACC1，由三垂线定理逆定理，得 A1C⊥AC1 ∴ A1ACC1 是菱形 ∴A1A=AC=a, A1D= a 2 3 . 13．如图，正三棱柱 AC1中，AB=2，D 是 AB 的中点，E 是 A1C1的中点，F 是 B1B 中点， 异面直线 CF 与 DE 所成的角为 90°. （1）求此三棱柱的高； （2）求二面角 C—AF—B 的大小. 解：（1）取 BC、C1C 的中点分别为 H、N，连结 HC1， 连结 FN，交 HC1 于点 K，则点 K 为 HC1 的中点，因 FN//HC，则△HMC∽△FMK，因 H 为 BC 中点 BC=AB=2，则 KN= 2 3, 2 1 FK ，∴ , 3 2 2 3 1  MK HM FK HC 则 HM= 15 1 HC ，在 Rt△HCC1，HC2=HM·HC1， 解得 HC1= 5 ，C1C=2. 另解：取 AC 中点 O，以 OB 为 x 轴，OC 为 y 轴，按右手系建立空间坐标系，设棱柱 高为 h ，则 C（ 0 ， 1 ， 0 ）， F （ 2 ,0,3 h ）， D（ 0, 2 1, 2 3  ）， E （ 0 ， 0 ， h ）， ∴ ), 2 1, 2 3(), 2 ,1,3( hCEhCF  ，由 CF⊥DE，得 0 22 1 2 3 2  hDECF ，解得 h=2. （2）连 CD，易得 CD⊥面 AA1B1B，作 DG⊥AF，连 CG， 由三垂线定理得 CG⊥AF，所以∠CGD 是二面角 C—AF—B 的平面角，又在 Rt△AFB 中，AD=1，BF=1，AF= 5 ， 从而 DG= , 5 5 ∴tan∠CGD= 15 DG DC ， 故二面角 C—AF—B 大小为 arctan 15 . A B B1 C1 A1 D C 14.已知 ABCD 是矩形，PD⊥平面 ABCD，PD=DC=a， 2AD a ，M、N 分别是 AD、PB 的中点。 （Ⅰ）求证：平面 MNC⊥平面 PBC； （Ⅱ）求点 A 到平面 MNC 的距离。 解：（I）连 PM、MB ∵PD⊥平面 ABCD ∴PD⊥MD…1 分 22222222 2 3 2 3 aAMABBMaMDPDPM  又 ∴PM=BM 又 PN=NB ∴MN⊥PB………3 分 ,22, BCaPCaBCaDCPD  得 NC⊥PB∴PB⊥平面 MNC……5 分 PB 平面 PBC ∴平面 MNC⊥平面 PBC……6 分 （II）取 BC 中点 E，连 AE，则 AE//MC∴AE//平面 MNC， A 点与 E 点到平面 MNC 的距离相等…7 分 取 NC 中点 F，连 EF，则 EF 平行且等于 2 1 BN ∵BN⊥平面 MNC ∴EF⊥平面 MNC，EF 长为 E 点到平面 MNC 的距离……9 分 ∵PD⊥平面 ABCD， BC⊥DC ∴BC⊥PC. 24 1 2 1,222 aPBBNEFaPCBCPB  即点 A 到平面 MNC 的距离为 2 a ……12 分 15．如图，正三棱柱 ABC—A1B1C1的底面边长的 3，侧棱 AA1= , 2 33 D 是 CB 延长线上一 点，且 BD=BC. （Ⅰ）求证：直线 BC1//平面 AB1D； （Ⅱ）求二面角 B1—AD—B 的大小； （Ⅲ）求三棱锥 C1—ABB1的体积. （Ⅰ）证明：CD//C1B1，又 BD=BC=B1C1， ∴ 四边形 BDB1C1是平行四边形， ∴BC1//DB1. 又 DB1平面 AB1D，BC1平面 AB1D， ∴直线 BC1//平面 AB1D. （Ⅱ）解：过 B 作 BE⊥AD 于 E，连结 EB1， ∵B1B⊥平面 ABD，∴B1E⊥AD ， ∴∠B1EB 是二面角 B1—AD—B 的平面角， ∵BD=BC=AB， ∴E 是 AD 的中点， . 2 3 2 1  ACBE 在 Rt△B1BE 中， .3 2 3 3 2 3 1 1  BE BBBEBtg ∴∠B1EB=60°。即二面角 B1—AD—B 的大小为 60° （Ⅲ）解法一：过 A 作 AF⊥BC 于 F，∵B1B⊥平面 ABC，∴平面 ABC⊥平面 BB1C1C， ∴AF⊥平面 BB1C1C，且 AF=  ,3 2 33 2 3 AFSVV CBBCBBAABBC   11111111 3 1 . 8 27 2 33)3 2 33 2 1( 3 1  即三棱锥 C1—ABB1 的体积为 . 8 27 解 法 二 ： 在 三 棱 柱 ABC—A1B1C1 中 ， 11111111111 CBAABAACABBCBAAABB VVVSS   . 8 27 2 33)3 4 34( 3 1 3 1 2 1111   AAS CBA 即三棱锥 C1—ABB1的体积为 . 8 27 16．如图，正三棱柱 ABC—A1B1C1，BC=BB1=1，D 为 BC 上一点， 且满足 AD⊥C1D. （I）求证：截面 ADC1⊥侧面 BC1； （II）求二面角 C—AC1—D 的正弦值； （III）求直线 A1B 与截面 ADC1 距离. （I）由题知： 11 1 1 1 11 BCADC ADCAD BCAD ADDC ADCC ABCAD ABCCC 面面 平面底面 底面                   ……………………………………………4 分 （II）              DCBCADC BCADC EFFDCCFC ACCE AACC EACCA 111 11 1 1 11 11 )( , 面又面 面知面由 连结于作过 为正方形面 点于与连结  故∠CEF 为二面角 C—AC1—D 的平面角…………………………………………6 分 在 Rt△C1CD 中，求出 5 10 2 2 5 5 sin, 5 5  CEFCF 故 ………………8 分 （III） ED CAE BCD ABC BCAD           中点为 中点为 为正三角形又 知由 1 ;,)( ∥A1B BA1 ∥面 AC1D，设 B 到面 ADC1 距离为 d……………………………………10 分 1DACCF 面 射影在面为斜线又 1ADCCEEF 1ACFE  I 5 5 3 1 3 1 1111   dCCSdSVV ABDADCABDCADCB …………………12 分 注：其他证法相应给分 17．如图，在底面是直角梯形的四棱锥 P ABCD 中，AD∥BC，∠ABC＝90°，且 ∠ADC  arcsin 5 5 ，又 PA⊥平面 ABCD，AD＝3AB＝3PA＝3a。 （I）求二面角 P—CD—A 的正切值； （II）求点 A 到平面 PBC 的距离。 P B C A D 解：（1）在底面 ABCD 内，过 A 作 AE⊥CD，垂足为 E，连结 PE P B A DH C E ∵PA⊥平面 ABCD，由三垂线定理知：PE⊥CD ∵∠PEA 是二面角 P—CD—A 的平面角………………2 分 在 Rt AED 中， AD a ADE  3 5 5 ， arcsin     AE AD ADE asin 3 5 5 ………………4 分 在 Rt PAE 中， tan  PEA PA AE 5 3 ∴二面角 P—CD—A 的正切值为 5 3 ………………6 分 （II）在平面 APB 中，过 A 作 AH⊥PB，垂足为 H ∵PA⊥平面 ABCD，∴PA⊥BC 又 AB⊥BC，∴BC⊥平面 PAB ∴平面 PBC⊥平面 PAB ∴AH⊥平面 PBC 故 AH 的长即为点 A 到平面 PBC 的距离………………10 分 在等腰直角三角形 PAB 中， AH a 2 2 ，所以点 A 到平面 PBC 的距离为 2 2 a …………12 分 18．直角梯形 ABCD 中，BC∥AD，AD∥⊥AB，BC BA AD m   1 2 ，VA⊥平面 ABCD。 （1）求证：VC⊥CD。 （2）若 VA m 2 ，求 CV 与平面 VAD 所成的角。 （1）连结 AC AB BC ABC CAB ACB o o        ， 90 45 取 AD 中点 G，连 CG，则 ABCG 为正方形 又CG GD CGD o  ， 90  DCG o45  DCA o90 …………………………（4 分） VA⊥平面 ABCD，DC⊥AC 由三垂线定理：VC⊥CD………………（6 分） （2）连 VG，由 CG AD VA CG CG       面 VAD CVG 是 CV 与平面 VAD 所成的角………………（9 分） VC VA AB BC m CG m CVG o        2 2 2 2 30， ∴CV 与平面 VAD 所成角为30o ………………………（12 分） 19．如图，在正四棱柱 ABCD—A1B1C1D1 中，AA1= 2 1 AB，点 E、M 分别为 A1B、C1C 的中 点，过点 A1，B，M 三点的平面 A1BMN 交 C1D1 于点 N. （Ⅰ）求证：EM∥平面 A1B1C1D1； （Ⅱ）求二面角 B—A1N—B1的正切值. （A）（Ⅰ）证明：取 A1B1 的中点 F，连 EF，C1F ∵E 为 A1B 中点 ∴EF∥ 2 1 BB1…………2 分 又∵M 为 CC1中点 ∴EF∥ C1M ∴四边形 EFC1M 为平行四边形 ∴EM∥FC1 ……4 分 而 EM 平面 A1B1C1D1 . FC1平面 A1B1C1D1 . ∴EM∥平面 A1B1C1D1………………6 分 （Ⅱ）由（Ⅰ）EM∥平面 A1B1C1D1 EM平面 A1BMN 平面 A1BMN∩平面 A1B1C1D1=A1N ∴A1N// EM// FC1 ∴N 为 C1D1 中点 过 B1 作 B1H⊥A1N 于 H，连 BH，根据三垂线定理 BH⊥A1N ∠BHB1 即为二面角 B—A1N—B1的平面角……8 分 设 AA1=a， 则 AB=2a， ∵A1B1C1D1为正方形 ∴A1H= a5 又∵△A1B1H∽△NA1D1 ∴B1H= 5 4 5 22 a a aa   在 Rt△BB1H 中，tan∠BHB1= 4 5 5 41 1  a a HB BB 即二面角 B—A1N—B1 的正切值为 4 5 ……12 分 （B）（Ⅰ）建立如图所示空间直角坐标系，设 AB=2a，AA1=a(a>0)，则 A1（2a，0，a），B（2a, 2a , 0）, C（0，2a，0），C1（0，2a，a）……2 分 ∵E 为 A1B 的中点，M 为 CC1的中点 ∴E（2a , a , 2 a ），M（0，2a, 2 a ） ∴EM// A1B1C1D1 …………6 分 （Ⅱ）设平面 A1BM 的法向量为 n =（x, y , z ） 又 BA1 =（0，2a , －a ） ) 2 ,0,2( aaBM  由 BMnBAn  ,1 ，得                2 4, 0 2 2 02 zy zx azax azay ), 2 , 4 ( aaan  …………9 分 而平面 A1B1C1D1的法向量为 )1,0,0(1 n .设二面角为 ，则 21 4 |||| ||cos| 1 1    nn nn  又：二面角为锐二面角 21 4cos   ，……11 分 从而 4 5tan  ………………12 分 20．如图，PA⊥平面 AC，四边形 ABCD 是矩形，E、F 分别是 AB、PD 的中点. （Ⅰ）求证：AF∥平面 PCE； （Ⅱ）若二面角 P—CD—B 为 45°，AD=2， CD=3，求点 F 到平面 PCE 的距离. （Ⅰ）取 PC 中点 M，连结 ME、MF. , 2 1 ,//, 2 1 ,// CDAECDAECDFMCDFM  FMAEFMAE  且,// ，即四边形 AFME 是平行四边形，……2/；‘。。。。分 ∴AF//EM，∵AF平在 PCE，∴AF∥平面 PCE.……4 分 （Ⅱ）∵PA⊥平面 AC，CD⊥AD，根据三垂线定理知，CD⊥PD ∴∠PDA 是二面角 P—CD—B 的平面角，则∠PDA=45°……6 分 于是，△PAD 是等腰直角三角形， AF⊥PD，又 AF⊥CD∴AF⊥面 PCD.而 EM//AF, ∴EM⊥面 PCD.又 EM平面 PEC, ∴面 PEC⊥面 PCD.……8 分 在面 PCD 内过 F 作 FH⊥PC 于 H，则 FH 为点 F 到平面 PCE 的距离.……10 分 由已知，PD=2 2 ，PF= .17,2 2 1  PCPD ∵△PFH∽△PCD ∴ . 17 343  FH PC CD PF FH ……12 分 21．如图，正三棱柱 AC1中，AB=2，D 是 AB 的中点，E 是 A1C1的中点，F 是 B1B 中点， 异面直线 CF 与 DE 所成的角为 90°. （1）求此三棱柱的高； （2）求二面角 C—AF—B 的大小. 解：（1）取 BC、C1C 的中点分别为 H、N，连结 HC1， 连结 FN，交 HC1 于点 K，则点 K 为 HC1 的中点，因 FN//HC，则△HMC∽△FMK，因 H 为 BC 中点 BC=AB=2，则 KN= 2 3, 2 1 FK ，∴ , 3 2 2 3 1  MK HM FK HC 则 HM= 15 1 HC ，在 Rt△HCC1，HC2=HM·HC1， 解得 HC1= 5 ，C1C=2. 另解：取 AC 中点 O，以 OB 为 x轴，OC 为 y 轴，按右手系建立空间坐标系，设棱柱 高为 h，则 C（0，1，0），F（ 2 ,0,3 h），D（ 0, 2 1, 2 3  ），E（0，0，h）， ∴ ), 2 1, 2 3(), 2 ,1,3( hCEhCF  ，由 CF⊥DE，得 0 22 1 2 3 2  hDECF ，解得 h=2. （2）连 CD，易得 CD⊥面 AA1B1B，作 DG⊥AF，连 CG， 由三垂线定理得 CG⊥AF，所以∠CGD 是二面角 C—AF—B 的平面角，又在 Rt△AFB 中，AD=1，BF=1，AF= 5 ， 从而 DG= , 5 5 ∴tan∠CGD= 15 DG DC ， 故二面角 C—AF—B 大小为 arctan 15 . 22．如图，正方体 1111 DCBAABCD  ，棱长为 a，E、F分别为 AB、BC上的点，且 AE＝ BF＝x． （1）当 x为何值时，三棱锥 BEFB 1 的体积最大？ （2）求三棱椎 BEFB 1 的体积最大时，二面角 BEFB 1 的正切值； （3）（理科做）求异面直线 EA1 与 FB1 所成的角的取值范围． （1） xxaaaxxaV BEFB )( 6 )( 2 1 3 1 1   24 ) 2 ( 6 3 2 axxaa    ，当 2 ax  时，三棱 锥 BEFB 1 的体积最大． （2）取 EF中点 O，由 EFOBEFBO  1， ，所以 OBB1 就是二面角 BEFB 1 的平面角．在 Rt△ BEF中 ，aaEFBO 2 2 2 2 2 1 2 1   22tan 1 1  BO BBOBB ． （3）在 AD上取点 H使 AH＝BF＝AE，则 11//// BACDHF ， 11BACDHF  ， FBHA 11 // ，所以 EHA1 （或补角）是异面直线 EA1 与 FB1 所 成的角；在 Rt△ AHA1 中， 22 1 xaHA  ，在 Rt△ AEA1 中， EA1 22 xa  ，在 Rt△HAE 中 ， xxxHE 222  ， 在 △ EHA1 中 ， EAHA EHEAHAEHA 11 22 1 2 1 1 2 cos    ，22 2 xa a   因为 ax 0 ，所以 2222 2aaxa  ， 1 2 1 22 2    ax a ， 1cos 2 1 1  EHA ， 3 π0 1  EHA 23． 已知，如图四棱锥 P—ABCD 中，底面 ABCD 是平行四边形，PG⊥平面 ABCD，垂足 为 G，G 在 AD 上，且 AG= 3 1 GD，BG⊥GC，GB=GC=2，E 是 BC 的中点，四面体 P—BCG 的体积为 3 8 . （Ⅰ）求异面直线 GE 与 PC 所成的角； （Ⅱ）求点 D 到平面 PBG 的距离； （Ⅲ）若 F 点是棱 PC 上一点，且 DF⊥GC，求 FC PF 的值. 解法一： （I）由已知 3 8 2 1 3 1 3 1   PGGCBGPGSV BCGBGCP ∴PG=4…………2′ 如图所示，以 G 点为原点建立空间直角坐标系 o—xyz， 则 B（2，0，0），C（0，2，0），P（0，0，4） 故 E（1，1，0） 10 10 202 2 |||| ,cos 3)4,2,0(),0,1,1(        PCGE PCGEPCGE PCGE  ∴异面直线 GE 与 PC 所成的角为 arccos 10 10 ……………………4′ （II）平面 PBG 的单位法向量 )0,1,0(0 n 6)0, 2 3, 2 3( 45,2 2 3|| 4 3||      GD CGDBCGD ∴点 D 到平面 PBG 的距离为 2 3|| 0  nGD ……………………8′ （III）设 F（0，y , z） 2 30) 2 3(2)0,2,0()0, 2 3, 2 3( 0, 01)0,2,0(), 2 3, 2 3()0, 2 3, 2 3(),,0(    yyy GCDFGCDF GCzyzyODOFDF  则 在平面 PGC 内过 F 点作 FM⊥GC，M 为垂足，则 2 1, 2 3  MCGM 3 MC GM FC PF ……………………………………………………………………12′ 解法二： （I）由已知 3 8 2 1 3 1 3 1   PGGCBGPGSV BCGBGCP ∴PG=4…………2′ 在平面 ABCD 内，过 C 点作 CH//EG 交 AD 于 H，连结 PH，则 ∠PCH（或其补角）就是异面直线 GE 与 PC 所成的角.………………3′ 在△PCH 中， 18,20,2  PHPCCH 由余弦定理得，cos∠PCH= 10 10 ∴异面直线 GE 与 PC 所成的角为 arccos 10 10 ……………………4′ （II）∵PG⊥平面 ABCD，PG平面 PBG ∴平面 PBG⊥平面 ABCD 在平面 ABCD 内，过 D 作 DK⊥BG，交 BG 延长线于 K，则 DK⊥平面 PBG ∴DK 的长就是点 D 到平面 PBG 的距离…………………………6′ 2 2 3 4 3 4 322  BCADGDBC 在△DKG，DK=DGsin45°= 2 3 ∴点 D 到平面 PBG 的距离为 2 3 ……………………………………8′ （III）在平面 ABCD 内，过 D 作 DM⊥GC，M 为垂足，连结 MF，又因为 DF⊥GC ∴GC⊥平面 MFD， ∴GC⊥FM 由平面 PGC⊥平面 ABCD，∴FM⊥平面 ABCD ∴FM//PG 由 GM⊥MD 得：GM=GD·cos45°= 2 3 …………………………10′ 33 2 1 2 3  FC PFGCDF MC GM FC PF 可得由 …………12′ 24．如图，已知正方体 ABCD－A1B1C1D1 的棱长为 2，M、N分别为 AA1、BB1的中点，求： （I）CM与 D1N所成角的余弦值； （II）异面直线 CM与 D1N的距离． 解：（I）如图，以 D为原点，DA、DC、DD1 分 别 为 x、y、z轴，建立空间直角坐标系，……………1′ 则 C（0，2，0）、D1（0，0，2）、M（2，0，1）、N （2，2，1）， ∴CM  ＝（2，－2，1）， 1DM  ＝（2， 2，－1）， ……………………3′ 设 CM与 D1N所成的角为α， 则 cosα＝ 1 1 CM 2 2 ( 2) 2 1 ( 1) 3 3|CM | | | D N D N              ＝－ 1 9 ＜0 ∴α为钝角，∴CM与 D1N所成的角为θ＝π－α，即 cosθ＝ 1 9 （解法 2：设 CM与 D1N所成的角为θ， 则 cosθ＝ 1 1 |CM | | 2 2 ( 2) 2 1 ( 1) | 3 3|CM | | | D N D N              ＝ 1 9 ） …………………………………6′ （II）取 DD1的中点 E，分别连接 EM、EB，则 EM∥BC，EB∥D1N， ∴B、C、E、M 共面且 D1N∥平面 BCEM， ∴D1到平面 BCEM 的距离 d 等于异面直线 CM 与 D1N 的距离， ……………………8、 ∵ 1 1 1 1 1D BCEM BAA CDD BAM CDE B NA DV V V V      ＝（ 2 1 ― 4 1 ― 1 12 ）·23＝ 3 4 …………10、 即 3 1 SBCEM·d＝ 3 4 而 SBCEM＝BM·BC＝2 5 ∴d＝ 2 5 5 ………………………………………………………………………………12、 解法 2： 设CM  ， 1D N  的法向量为 n  ＝（x，y，z） 则 2 2 0 2 2 0 x y z x y z         0 2 x z y    ， 取 n  ＝（0，1，2）……………………………………………………………………………8′ ∴异面直线 CM与 D1N的距离 d＝ 1| | 2 2 5 5| | 5 DM n n      ……………………………12′ 25．如图，四棱锥 P—ABCD 的底面是正方形,PA⊥底面 ABCD，PA=AD=2，点 M、N 分别 在棱 PD、PC 上，且 PC⊥平面 AMN. （Ⅰ）求证：AM⊥PD； （Ⅱ）求二面角 P—AM—N 的大小； （Ⅲ）求直线 CD 与平面 AMN 所成角的大小. （I）证明：∵ABCD 是正方形，∴CD⊥AD， ∵PA⊥底面 ABCD，∴PA⊥CD. ∴CD⊥平面 PAD……………………………………3 分 ∵AM平面 PAD，∴CD⊥AM. ∵PC⊥平面 AMN，∴PC⊥AM. ∴AM⊥平面 PCD. ∴AM⊥PD.…………………………………………5 分 （II）解：∵AM⊥平面 PCD（已证）. ∴AM⊥PM，AM⊥NM. ∴∠PMN 为二面角 P-AM-N 的平面角.…………………………7 分 ∵PN⊥平面 AMN，∴PN⊥NM. 在直角△PCD 中，CD=2，PD=2 2 ，∴PC=2 3 . ∵PA=AD，AM⊥PD，∴M 为 PD 的中点，PM= 2 1 PD= 2 由 Rt△PMN∽Rt△PCD，得 ∴ PC PMCDMN   . . 3 3arccos. 3 3 32 2)cos(  PMN PC CD PM MNPMN …………10 分 即二面角 P—AM—N 的大小为 3 3arccos . （III）解：延长 NM，CD 交于点 E. ∵PC⊥平面 AMN，∴NE 为 CE 在平面 AMN 内的射影 ∴∠CEN 为 CD（即（CE）与平在 AMN 所成的角.…………12 分 ∵CD⊥PD，EN⊥PN，∴∠CEN=∠MPN. 在 Rt△PMN 中， . 3 3arcsin) 2 ,0( . 3 3)sin(   MPNMPN PM MNMPN  ∴CD 与平面 AMN 所成的角的大小为 3 3arcsin …………15 分 26．如图，直三棱柱 ABC—A1B1C1中， 0 190 , 2, 4ACB BC AC AA     ，D 为棱 CC1 上的一动点，M、N 分别为 1 1,ABD AB D  的重心． （1）求证：MN BC ； （2）若二面角 C—AB—D 的大小为 arctan 2 ，求点 C1到平面 A1B1D 的距离； （3）若点 C 在 ABD 上的射影正好为 M，试判断点 C1在 1 1A B D 的射影是否 为 N？并说明理由． N D C B A1 A B1 C1 M 解：（1）连结 ,DM DN并延长，分别交 1 1,AB A B 于 ,P Q，连结 PQ， ,M N 分别为 1 1,ABD AB D  的重心，则 ,P Q分别为 1 1,AB A B 的中点 1//PQ BB  在直三棱柱 1 1 1ABC A BC 中， 1BB BC MN BC   （2）连结 1CP AC BC CP AB CC ABC DP AB      又 面 CPD 即为二面角C AB D  的平面角 arctan 2CPD  在 Rt ABC 中， 2 2AC BC CP    tan 2Rt CDP CD CP CPD     在 中， 1 1 14 2CC AA DC    连结 2 2 1 1 1 1, 2 6CQ CQ CP DQ DC CQ      同上可知， 1 11 1 1 2 3 2A B DDQ AB S AB DQ     设 1 1 1C DAB h到面 的距离为 1 1 1 1 1 1C A B D D A B CV V  1 1 1 1 11A B D A B Ch S C D S     2 3 3 h  （3） 2 1 1 2 1 , 2 2 CP PMC M ABD C M DP CP CD MD       面 12 2CD C D    //DQ DP MN PQ DM DN  则 2 2 1CD DM DP DC DN DQ     1DCQ ∽ 1 1 1 90DNC C ND DC Q      1 1 1 1C N DQ AB C CPQ  又 面 1 1 1 1 1 1A B C N C N AB D   面 1 1 1C AB D N 在面 的射影即为 . （另解）[9(B)]空间向量解法：以 C1 为原点，如图建立空间 直角坐标系。 （1） 设  1 0 4C D a a   ，依题意有：          10,0, , 2,0,4 , 0,2,4 , 0,0,4 , 0,0,0D a A B C C 因为 M、N 分别为 1 1,ABD AB D  的重心． 所以 2 2 8 2 2 8, , , , , 0,0, 3 3 3 3 3 3 3 a aM N NM                   ∵ )0,1,0( 3 8,0,0      CBNM ∴MN BC （2） 因为平面 ABC 的法向量  1 0,0, 1n    ， 设平面 ABD 的法 向量  2 1 1 1, ,n x y z                      1212 111 111 2 2 4 2,, 0),,()0,2,2( 0),,()4,0,2( 0 0 x a xxn zyx zyxa nAB nAD N D C B A1 A B1 C1 M P Q P Q C C1D NM N M D C 1 B1 A1 C B A z y x A E C D FB 令 1 2 21 1,1, 4 x n a         ，设二面角 C—AB—D 为 ，则由 3tan 2 cos 3     因此 2 3 3 36162 2 4 22 4 2 cos 22 21 21                a aa a a nn nn  设平面 A1B1D 的法向量为  3 , ,n x y z  ，则 )1,1,1(1),,( 0),,()0,2,2( 0),,()2,0,2( 0 0 33 311 31              nxxxxn zyx zyx nBA nDA 有令 设 C1 到平面 A1B1D 的距离为 d ，则 3 32 || 3 31    n nDCd （3）若点 C 在平面 ABD 上的射影正好为 M，则 0 ADCMADCM 即 6,2 3 4 3 )4(0)4,0,2( 3 4, 3 2, 3 2 2          aaaaa （舍） 因为 D 为 CC1的中点，根据对称性可知 C1在平面 A1B1D 的射影正好为 N。 27．在 RtABC 中， ACB=30  ， B=90 ，D 为 AC 中点，E 为 BD 的中点，AE 的延 长线交 BC 于 F， 将ABD 沿 BD 折起，二面角 A－BD－C 大小记为 。 （1） 求证：面 AEF面 BCD； （2）  为何值时，AB CD。 （1）证明：在 RtABC 中， C=30 ，D 为 AC 的中点，则ABD 是等边三角形又因 E 是 BD 的中 点， BD AE，BD EF，折起后，AE EF=E， BD面 AEF BD面 BCD，面 AEF 面 BCD。 （2）过 A 作 AP面 BCD 于 P，则 P 在 FE 的延长线上，设 BP 与 CD 相交于 Q，令 AB=1，则ABD 是边长为 1 的等边三角形，若 AB CD，则 BQ CD PE= 3 1 AE= 3 3 又 AE= 2 3 · B A P CF D O E P 折后有 cosAEP= AE PE = 3 1 由于AEF= 就是二面角 A－BD－C 的平面角， 当 = －arccos 3 1 时，AB CD 28．如图，在斜三棱柱 ABC－A1B1C1 中，侧面 AA1B1B⊥底面 ABC， 侧棱 AA1与底面 ABC 成 600的角， AA1= 2．底面 ABC 是边长为 2 的正三角形，其重 心 为 G 点。E 是线段 BC1上一点，且 BE= 3 1 BC1 ． （１）求证： GE∥侧面 AA1B1B ； （２）求平面 B1GE 与底面 ABC 所成锐二面角的大小 解法 1：(1)延长 B1E 交 BC 于 F, ∵ΔB1EC∽ΔFEB, BE＝ 2 1 ＥＣ１ ∴ＢＦ＝ 2 1 Ｂ１Ｃ１＝ 2 1 ＢＣ，从而Ｆ为ＢＣ的中点． …………… ……………２′ ∵Ｇ为ΔＡＢＣ的重心，∴Ａ、Ｇ、Ｆ三点共线，且 FA FG ＝ 1FB FE ＝ 3 1 ，∴GE∥AB1， 又 GE侧面 AA1B1B， ∴GE∥侧面 AA1B1B ……………… ………６＇ （２）在侧面 AA1B1B 内，过 B1 作 B1Ｈ⊥ＡＢ，垂足为Ｈ，∵侧面 AA1B1B⊥底面 ABC， ∴B1Ｈ⊥底面 ABC．又侧棱 AA1 与底面 ABC 成 600的角， AA1= 2， ∴∠B1ＢＨ＝６０ ０ ，ＢＨ＝１，B1Ｈ＝ 3 ． 在底面 ABC 内，过Ｈ作ＨＴ⊥ＡＦ，垂足为Ｔ，连 B1Ｔ．由三垂线定理有 B1Ｔ⊥ＡＦ， 又平面 B1GE 与底面 ABC 的交线为ＡＦ，∴∠B1ＴＨ为所求二面角的平面角．……９＇ ∴ＡＨ＝ＡＢ＋ＢＨ＝３，∠ＨＡＴ＝３０ ０ ， ∴ＨＴ＝ＡＨsin300＝ 2 3 ， 在ＲｔΔB1ＨＴ中，ｔａｎ∠B1ＴＨ＝ HT HB1 ＝ 3 32 ， 从而平面 B1GE 与底面 ABC 所成锐二面角的大小为 arctan 3 32 ……………… 12′ 解法 2：（１）∵侧面 AA1B1B⊥底面 ABC，侧棱 AA1与底面 ABC 成 600 的角， ∴∠A1AB＝６０ ０ ，又 AA1= ＡＢ= 2，取ＡＢ的中点Ｏ,则ＡＯ⊥底面 ABC． 以 O 为原点建立空间直角坐标系 O－ｘｙｚ如图， 则Ａ（０，－１，０），Ｂ（０，１，０），Ｃ（ 3 ，０，０）， Ａ１（０，０， 3 ）Ｂ１（０，２， 3 ），Ｃ１（ 3 ，１， 3 ）． ……３＇ ∵Ｇ为ΔＡＢＣ的重心，∴Ｇ（ 3 3 ，０，０）， ∵ BE＝ 3 1 1BC ∴Ｅ（ 3 3 ，１， 3 3 ）∴GE＝（０，１， 3 3 ）＝ 3 1 1AB ， 又 GE侧面 AA1B1B， ∴GE∥侧面 AA1B1B …………… ……６＇ （２）设平面 B1GE 的法向量为ｎ＝（ａ，ｂ，ｃ）， 则由ｎ· EB1 ＝０及ｎ·GE＝０得 3 3 ａ－ｂ－ 3 32 ｃ＝０；ｂ＋ 3 3 ｃ＝０． 可取ｎ＝（ 3 ，－１， 3 ）． ……………8＇ 又底面 ABC 的法向量为ｍ＝（０，０，１）， ……………9′ 设平面 B1GE 与底面 ABC 所成锐二面角的大小为 ， 则 cos ＝ |||| nm nm   ＝ 7 21 , ∴ ＝arccos 7 21 . ……………… 12’ 29．已知三棱锥 P—ABC 中 PB⊥底面 ABC，  90BCA ， PB=BC=CA=a，E 是 PC 的中点，点 F 在 PA 上，且 3PF=FA. （1）求证：平面 PAC⊥PBC； （2）求平面 BEF 与底面 ABC 所成角（用一个反三角函数值表示）. （1）证明：∵PB⊥底面 ABC，∴PB⊥AC…………1 分，又∠BCA=90° ∴AC⊥平面 PBC…………4 分 又 AC平面 PAC，∴平面 PAC⊥平面 PBC…………5 分 （2）解：设 FE 的延长线与 AC 的延长线交于 M，连 MB， 则 MB 为平面 BEF 与平面 ABC 的交线…………6 分 在平面 PCA 中，由已知 E 是 PC 的中点，F 是 PA 的四等分点， aACMC 2 1 2 1  …………7 分 取 BC 的中点 H，则 EH//PB， ∴EH⊥底面 ABC…………8 分 过 H 作 HO⊥MB 于 O，由三垂线定理，EO⊥MB 则∠EOH 为平面 BEF 与底面 ABC 所成二面角的平面角…………9 分 在 aHOBCMRt 10 5,  中 ，在 aEHEHORt 2 1,....  中 …………10 分 5tan  HO EHEOH …………11 分 即平面 BEF 与底面 ABC 所成二面角的大小为 5arctan …………12 分 若利用面积射影法，指出△HDB 是△EFB 在底面 ABC 上的射影，并计算出其面积 2 16 1 aS 射影 …………7 分 计算出 2 16 6 aS EFB  …………10 分 6 1cos  EFBS S射影 …………11 分 即平面 BEF 与底面 ABC 所成二面角的大小为 6 6arccos …………12 分 30．三棱锥 ABCS  中，底面△ ABC 是顶角为 ABC 、 aAC  的等腰△， 2  SCA ， bSC  ，侧面 SAC与底面 ABC所成二面角为 E) 2 0(   、D分别为 SA 和 AC的中点 (1)求证无论 ，为何值时，点 S到截面BDE的距离为定值 (2)求三棱锥 ABCS  的体积 (理)(1)∵ E、D为中点，∴ ED∥ SC ，∴ SC ∥面 BDE ∴ S 到截面 BDE的距离 为C到截面 BDE的距离. 又 ,ACSC  ∴ .ACED  ∵ ,ACAB  ∴ ,ACBD  ∴ AC 面BDE ∴C到截面 BDE的距离为 ,aCD 2  即 S到截面BDE的距离为 . 2 a (2)由(1)知 BDE ,又 , 2 1 2 1 bSCED  ∴ E到 ABC的距离为 .sin 2 b aBDADS ABD 2 1 2 1 2 1  ,actgaaactg 28 1 22 1 2 ∴ .sin 212 1sin 228 1 3 144 22  abctgabactgaVV ABDEABCS  