- 103.00 KB
- 2021-05-13 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
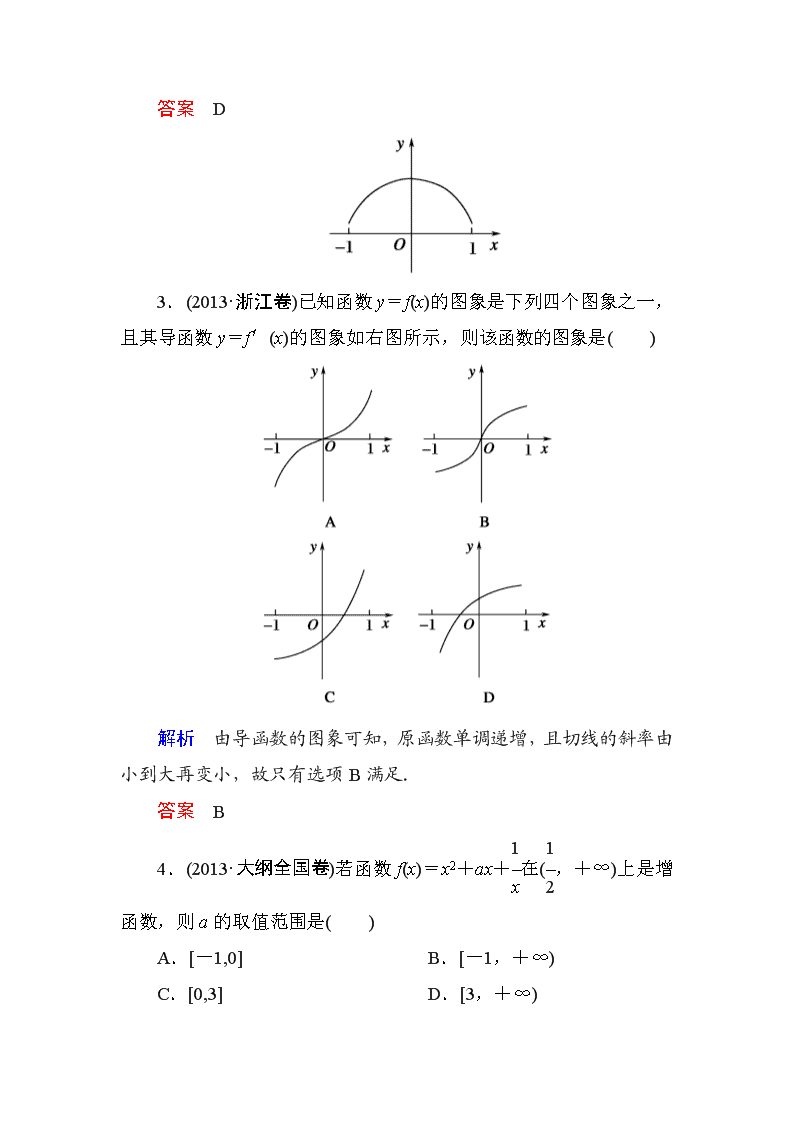
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
第十二节 导数的应用(一)
时间:45分钟 分值:75分
一、选择题(本大题共6小题,每小题5分,共30分)
1.函数f(x)=x+elnx的单调递增区间为( )
A.(0,+∞) B.(-∞,0)
C.(-∞,0)和(0,+∞) D.R
解析 函数定义域为(0,+∞),f′(x)=1+>0,故单调增区间是(0,+∞).
答案 A
2.设函数f(x)=+lnx,则( )
A.x=为f(x)的极大值点
B.x=为f(x)的极小值点
C.x=2为f(x)的极大值点
D.x=2为f(x)的极小值点
解析 函数f(x)的定义域为(0,+∞),
f′(x)=-+=,
当x=2时,f′(x)=0;当x>2时,f′(x)>0,函数f(x)为增函数;
当0),g′(x)=--2<0,故g(x)在(,+∞)上为减函数,所以a≥g()=3.故选D.
答案 D
5.(2013·浙江卷)已知e为自然对数的底数,设函数f(x)=(ex-1)(x-1)k(k=1,2),则( )
A.当k=1时,f(x)在x=1处取到极小值
B.当k=1时,f(x)在x=1处取到极大值
C.当k=2时,f(x)在x=1处取到极小值
D.当k=2时,f(x)在x=1处取到极大值
解析 当k=1时,f(x)=(ex-1)(x-1),f′(1)=xex-1,x=1不是f′(x)=0的根,所以不是极值点,排除A、B;当k=2时,f(x)=(ex-1)(x-1)2,f′(x)=(x-1)(xex+ex-2),当x=1时f′(x)=0且x>1时f′(x)>0,结合选项,故选C.
答案 C
6.(2013·湖北卷)已知函数f(x)=x(lnx-ax)有两个极值点,则实数a的取值范围是( )
A.(-∞,0) B.
C.(0,1) D.(0,+∞)
解析 f′(x)=lnx-ax+x=lnx-2ax+1,假设函数f(x)只有1个极值点,则方程lnx-2ax+1=0(x>0)只有一根,数形结合,即直线y=2ax-1与曲线y=lnx相切.设切点为(x0,lnx0),则切线方程为
y-lnx0=(x-x0),即y=x+lnx0-1.又切线方程为y=2ax-1,对比得解得a=,x0=1.故若要使直线y=2ax-1与曲线y=lnx相交,即函数f(x)=x(lnx-ax)有2个极值点,需满足00.所以m>6或m<-3.
答案 (-∞,-3)∪(6,+∞)
9.已知函数f(x)=(m-2)x2+(m2-4)x+m是偶函数,函数g(x)=-x3+2x2+mx+5在(-∞,+∞)内单调递减,则实数m=________.
解析 若f(x)=(m-2)x2+(m2-4)x+m是偶函数,
则m2-4=0,m=±2.
若g′(x)=-3x2+4x+m≤0恒成立,
则Δ=16+4×3m≤0,解得m≤-,故m=-2.
答案 -2
三、解答题(本大题共3小题,每小题10分,共30分)
10.已知函数f(x)=ax2+blnx在x=1处有极值.
(1)求a,b的值;
(2)求函数y=f(x)的单调区间.
解 (1)f′(x)=2ax+.又f(x)在x=1处有极值.
得即
解之得a=,b=-1.
(2)由(1)可知f(x)=x2-lnx,其定义域是(0,+∞),
且f′(x)=x-=.
由f′(x)<0,得00,得x>1.
所以函数y=f(x)的单调减区间是(0,1),单调增区间是(1,+∞).
11.(2013·福建卷)已知函数f(x)=x-alnx(a∈R).
(Ⅰ)当a=2时,求曲线y=f(x)在点A(1,f(1))处的切线方程;
(Ⅱ)求函数f(x)的极值.
解 函数f(x)的定义域为(0,+∞),f′(x)=1-.
(Ⅰ)当a=2时,f(x)=x-2lnx,f′(x)=1-(x>0),
因而f(1)=1,f′(1)=-1,
所以曲线y=f(x)在点A(1,f(1))处的切线方程为y-1=-(x
-1),即x+y-2=0.
(Ⅱ)由f′(x)=1-=,x>0知:
①当a≤0时,f′(x)>0,函数f(x)为(0,+∞)上的增函数,函数f(x)无极值;
②当a>0时,由f′(x)=0,解得x=a,
又当x∈(0,a)时,f′(x)<0;当x∈(a,+∞)时,f′(x)>0,
从而函数f(x)在x=a处取得极小值,且极小值为f(a)=a-alna,无极大值.
综上,当a≤0时,函数f(x)无极值;
当a>0时,函数f(x)在x=a处取得极小值a-alna,无极大值.
12.(2014·石家庄质检)已知函数f(x)=2x3-3(a+1)x2+6ax(a∈R).
(1)当a=2时,求函数y=f(x)的单调区间;
(2)若a>0时,函数y=f(x)在闭区间[0,a+1]上的最大值为f(a+1),求a的取值范围.
解 (1)当a=2时,f(x)=2x3-9x2+12x,
f′(x)=6x2-18x+12=6(x2-3x+2)
=6(x-1)(x-2).
由f′(x)>0,得x<1或x>2.
由f′(x)<0,得1<x<2.
所以,f(x)的递增区间为(-∞,1),(2,+∞),递减区间为(1,2).
(2)f′(x)=6x2-6(a+1)x+6a=6[x2-(a+1)x+a]=6(x-1)(x-a).
当a=1时,f′(x)≥0,f(x)在[0,a+1]上单调递增,最大值为f(a+1).
当0<a<1时,x,f′(x),f(x)的变化情况如下表:
x
0
(0,a)
a
(a,1)
1
(1,1+a)
1+a
f′(x)
+
0
-
0
+
f(x)
↗
极大值
↘
极小值
↗
由上表可知,f(x)在[0,a+1]上的最大值只有可能是f(a)或f(a+1).
故只需f(a+1)-f(a)=(-a3+3a2+3a-1)-(-a3+3a2)=3a-1≥0.
解得a≥,此时≤a<1.
当a>1时,x,f′(x),f(x)的变化情况如下表:
x
0
(0,1)
1
(1,a)
a
(a,a+1)
a+1
f′(x)
+
0
-
0
+
f(x)
↗
极大值
↘
极小值
↗
由上表可知,f(x)在[0,a+1]上的最大值只有可能是f(1)或f(a+1).
故只需f(a+1)-f(1)=(-a3+3a2+3a-1)-(3a-1)=-a3+3a2≥0.
解得a≤3,此时1<a≤3.
综上,a的取值范围是.
相关文档
- 2014年版高考英语代词语法考点练习2021-05-1314页
- 2017年度高考生物(细胞呼吸和光合作2021-05-133页
- 高考化学三轮复习模拟试题元素化合2021-05-1312页
- 2020-2021学年高考数学(理)考点:导数2021-05-1343页
- 高考数学重点难点讲解三运用向量法2021-05-136页
- 奇速英语高考英语单项选择点拨精选2021-05-136页
- 2014年版高考生物专题目26传统发酵2021-05-133页
- 人教高考化学一轮选练习题7及答案2021-05-135页
- 河北省高考物理二轮练习专题1万有2021-05-1311页
- 数学高考试题分析 专题六 导数及2021-05-136页