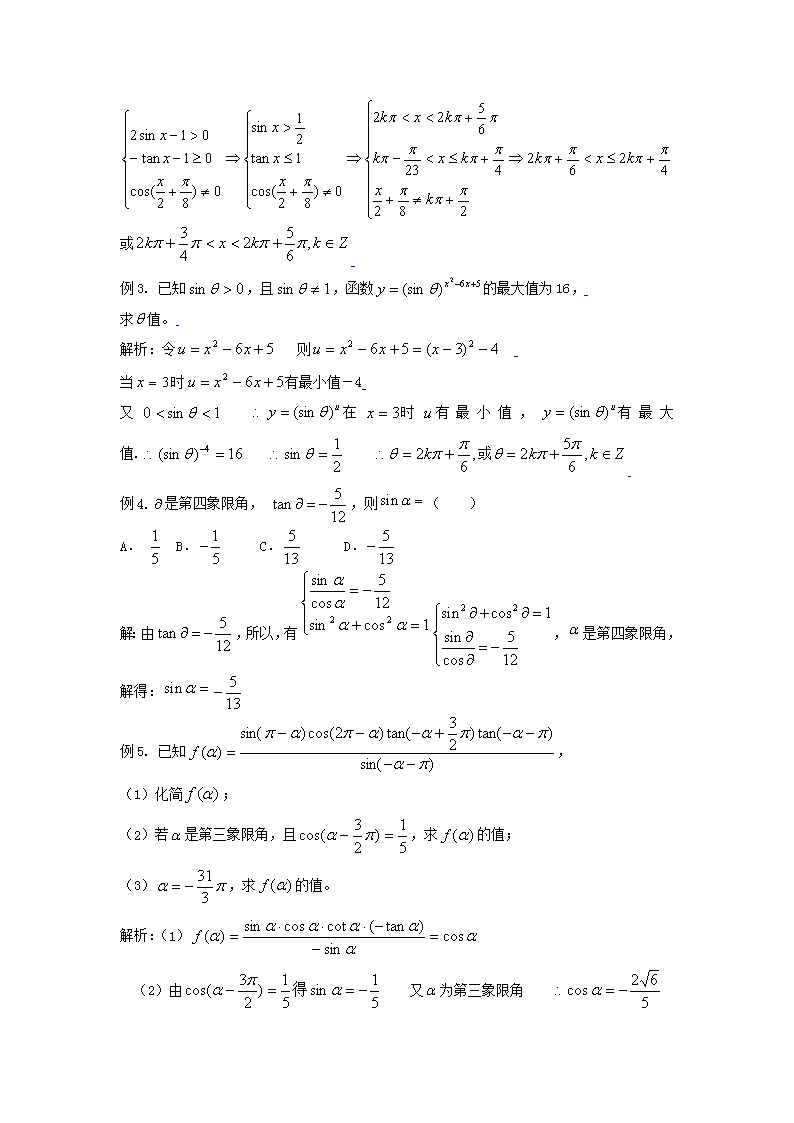高考二轮复习数学三角函数 7页

基本初等函数Ⅱ（三角函数） ‎【专题要点】任意角的概念和弧度制、任意角的三角函数的定义（重点是任意角的正弦、余弦和正切的定义）、周期函数的概念、三角函数（正弦函数、余弦函数和正切函数）的图象与性质、函数的图象和性质、同角三角函数的基本关系式和诱导公式. ‎【考纲要求】 ‎（1）任意角的概念、弧度制 ‎①了解任意角的概念，②了解弧度制概念，能进行弧度与角度的转化. ‎（2）三角函数 ‎①理解任意角的三角函数的定义； ‎②能利用单位圆中的三角函数线推导出的正弦、余弦、正切的诱导公式，能画出正、余弦函数、正切函数的图象，了解三角函数的周期性； ‎③理解正、余弦函数在]0，2π]，正切函数在（-，）的性质，如单调性、最大值与最小值、周期性，图象与x轴的交点； ‎④理解同角三角函数的基本关系式； ‎⑤了解的物理意义，能画出的图象，了解参数、、对函数图象变化的影响； ‎⑥了解三角函数是描述周期性变化现象的重要函数模型，会用三角函数解决一些简单的问题。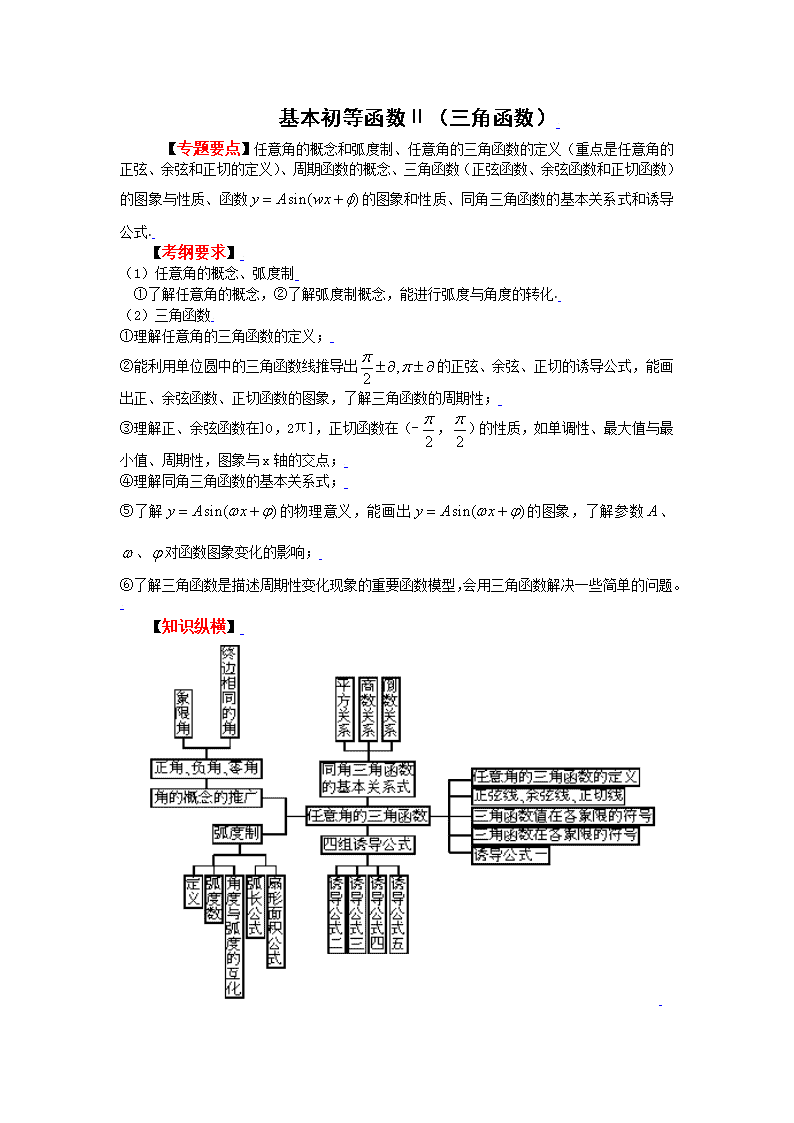 ‎【知识纵横】 ‎【教法指引】 高考对三角函数的考查内容稳定，难度稳定，题量稳定，题型稳定，注重创新。因此，我们在复习中应首先立足课本，打好基础，从数形两方面理解三角函数的定义，在牢固图象的基础上，把握三角函数的性质，通过认识整个体系的推导和形成过程，掌握公式的本质和规律，领会其中的数学思想，形成清晰的知识结构，明确各部分的基本知识，基本题型，基本方法和规律，强化易混、易漏、易错点的反思和感悟和针对性训练；其次，在学习过程中不断总结、反思提炼解题规律，学会观察差异，寻找联系，分析综合，合理转化，会从三角函数的名称、角和运算三个方面寻求解题思路；另外，注意重点问题的变式、拓展和延伸，突出复习的针对性和有效性，在解题时，注意在条件和结论中建立联系，讲求算理，就能立足基础、发展能力、决胜高考. ‎【典例精析】 例1.若角的终边落在直线上，求的值. 解析：【解法一】分类讨论 ‎①角的终边在第二象限 则； ‎②角的终边在第二象限 则. ‎【解法二】也可以按照课本上三角函数的定义，求出终边与单位圆的交点。 例2.求下列函数的定义域。 ‎（1） （2）（3） 解析：（1）要使函数有意义 ，那么的终边在第一或第二象限，或终边在轴上. ‎（2）要使函数有意义，那么解得： ‎（3）要使函数有意义，那么 或 例3. 已知，且，函数的最大值为16， 求值。 解析：令 则 当时有最小值－4 又 在时有最小值，有最大值. 或 例4.是第四象限角， ，则（ ）‎ A． B． C． D．‎ 解：由，所以，有，是第四象限角，‎ 解得：‎ 例5. 已知，‎ ‎（1）化简；‎ ‎（2）若是第三象限角，且，求的值；‎ ‎（3），求的值。‎ 解析：（1）‎ ‎ （2）由 又为第三象限角 ‎ ‎（3） ‎ 例6.已知　求 ‎　⑴；‎ ‎⑵‎ 解析：【解法一】由得 ‎⑴＝‎ ‎⑵＝＝‎ ‎【解法二】也可以对进行分类讨论，得到的关系，再利用，解出.‎ 例7. 已知，且是方程的两根，求 的值。‎ 解析：由题意 例8. 使函数图象上每一点的纵坐标保持不变，横坐标缩小到原来的，然后再将其图象沿轴向左平移个单位，得到的曲线与相同.‎ ‎（1）求的表达式；‎ ‎（2）求的单调递减区间.‎ 解析：（1）的图象沿轴向右平移个单位得：即 ‎，再将每一点的纵坐标保持不变，横坐标扩大到原来的2倍得 ‎.‎ ‎（2）由 ‎ 解得 ‎ 函数的单调递减区间是 例9. 已知函数（其中）的最小正周期为2，且当时，取得最大值2.‎ ‎（1）求函数的表达式；‎ ‎（2）在闭区间上是否存在的对称轴？如果存在，求出其对称轴方程；如果不存在，说明理由.‎ 解析：（1）‎ ‎ 由题意 ： 又 ‎ 又 ‎ ‎ 解得： ‎ ‎ ‎ ‎ （2）由＝ 得：‎ ‎ 由得 又 ‎ 在闭区间上存在的对称轴.‎ 例10. 若则=( )‎ ‎（A） （B）2 （C） （D）‎ 解析：由可得：由，‎ 又由，可得：＋（）2＝1‎ 可得＝－，＝－，‎ 所以，＝＝2。‎ 例11. 函数的图象是（ ）‎ y x O y x O y x O y x O A．‎ B．‎ C．‎ D．‎ 解析：是偶函数，可排除B、D，由的值域可以确定.因此本题应选A.‎ 点评：本小题主要考查复合函数的图像识别，充分掌握偶函数的性质，余弦函数的图象及性质，另外，排除法，在复习时应引起重视，解选择题时，经常采用排除法。‎ 例12. 把函数的图象上所有的点向左平行移动个单位长度，再把所得图象上所有点的横坐标缩短到原来的倍（纵坐标不变），得到的图象所表示的函数是（ ）‎ A． B．‎ C． D．‎ 解析：‎ y=，故选（C）。‎ 点评：三角函数图象的平移、伸缩变换是高考的热门试题之一，牢固变换的方法，按照变换的步骤来求解即可.‎ 例13.在同一平面直角坐标系中，函数的图象和直线的交点个数是( 　 )‎ ‎（A）0 （B）1 （C）2 （D）4‎ 解析：原函数可化为：=作出原函数图像，‎ 截取部分，其与直线的交点个数是2个.‎ 点评：本小题主要考查三角函数图像的性质问题，学会五点法画图，取特殊角的三角函数值画图.‎ w.w.w.k.s.5.u.c.o.m ‎ www.ks5u.com