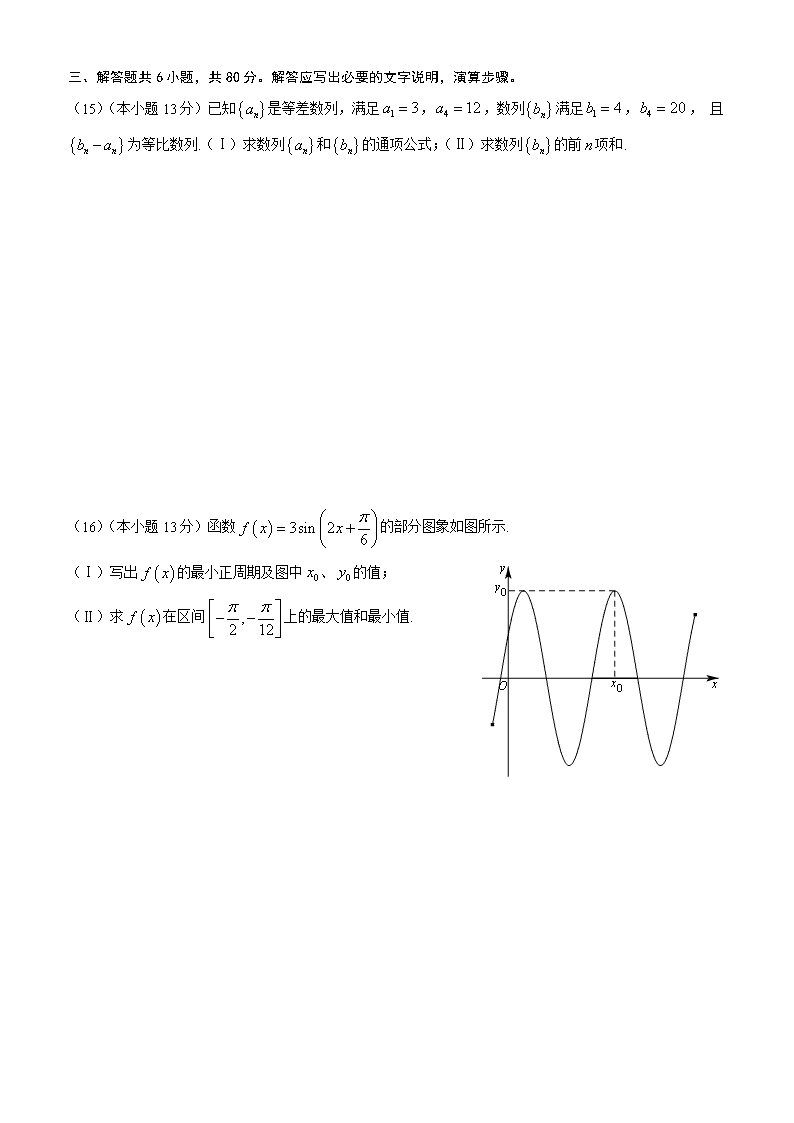北京高考数学文科试题及答案 9页

绝密★启封并使用完毕前 ‎2014年普通高等学校招生全国统一考试 数学（文）（北京卷）‎ 本试卷共5页，150分。考试时长120分钟，考生务必将答案答在答题卡上，在试卷上作答无效。考试结束后，将本试卷和答题卡一并收回。‎ 第一部分（选择题 共40分）‎ 一、 选择题共8小题，每小题5分，共40分。在每小题列出的四个选项中，选出符合题目要求的一项。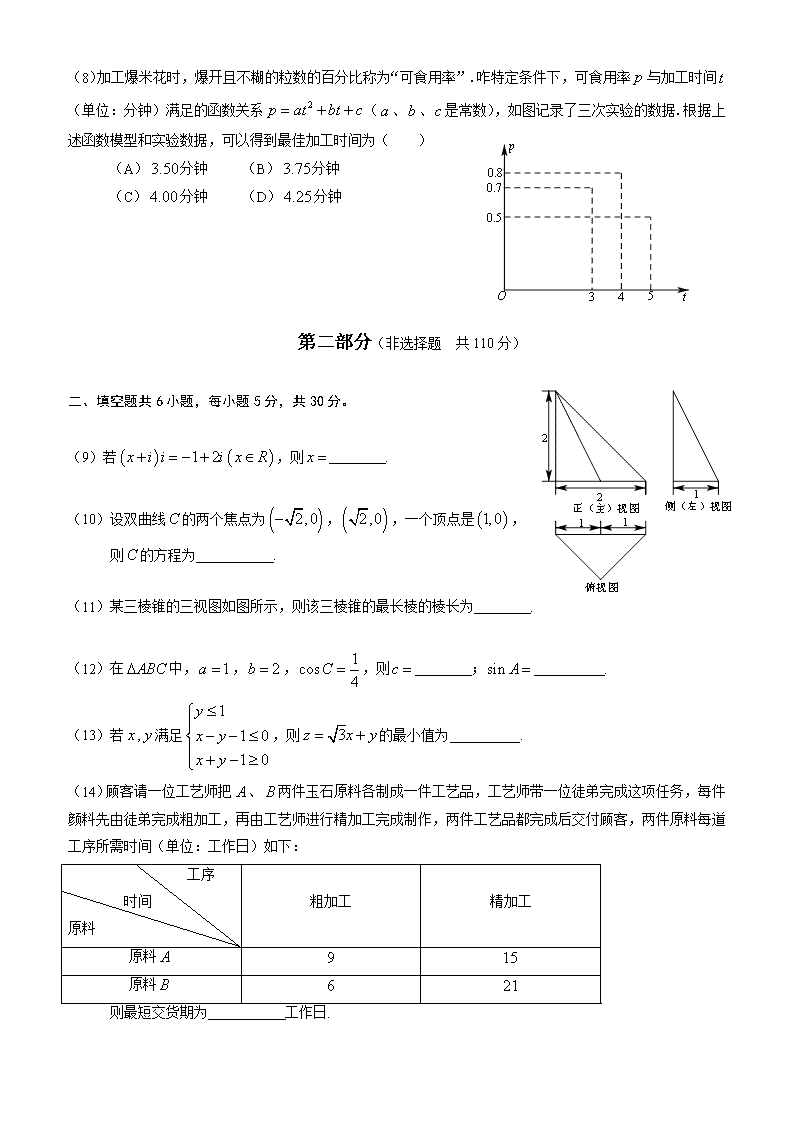‎ ‎（1）若集合，，则（ ）‎ ‎ （A） （B） （C） （D）‎ ‎（2）下列函数中，定义域是且为增函数的是（ ）‎ ‎ （A） （B） （C） （D）‎ ‎（3）已知向量，，则（ ）‎ ‎ （A） （B） （C） （D）‎ ‎（4）执行如图所示的程序框图，输出的值为（ ）‎ ‎ （A） （B） （C） （D）‎ ‎（5）设、是实数，则“”是“”的（ ）‎ ‎(A) 充分而不必要条件 (B) 必要而不必要条件 ‎ (C) 充分必要条件 (D) 既不充分不必要条件 ‎（6）已知函数，在下列区间中，包含零点的区间是（ ）‎ ‎ (A) (B) (C) (D)‎ ‎（7）已知圆和两点，，若圆上存在点，使得，则的最大值为（ ）‎ ‎ （A） （B） （C） （D）‎ ‎（8）加工爆米花时，爆开且不糊的粒数的百分比称为“可食用率”.咋特定条件下，可食用率与加工时间（单位：分钟）满足的函数关系（、、是常数），如图记录了三次实验的数据.根据上述函数模型和实验数据，可以得到最佳加工时间为（ ）‎ ‎ （A）分钟 （B）分钟 ‎ ‎（C）分钟 （D）分钟 第二部分（非选择题 共110分）‎ 二、填空题共6小题，每小题5分，共30分。‎ ‎（9）若，则 .‎ ‎（10）设双曲线的两个焦点为，，一个顶点是，‎ 则的方程为 .‎ ‎（11）某三棱锥的三视图如图所示，则该三棱锥的最长棱的棱长为 .‎ ‎（12）在中，，，，则 ； .‎ ‎（13）若,满足，则的最小值为 .‎ ‎（14）顾客请一位工艺师把、两件玉石原料各制成一件工艺品，工艺师带一位徒弟完成这项任务，每件颜料先由徒弟完成粗加工，再由工艺师进行精加工完成制作，两件工艺品都完成后交付顾客，两件原料每道工序所需时间（单位：工作日）如下：‎ ‎ 工序 ‎ 时间 原料 粗加工 精加工 原料 原料 则最短交货期为 工作日.‎ 三、解答题共6小题，共80分。解答应写出必要的文字说明，演算步骤。‎ ‎（15）（本小题13分）已知是等差数列，满足，，数列满足，， 且为等比数列.（Ⅰ）求数列和的通项公式；（Ⅱ）求数列的前项和.‎ ‎（16）（本小题13分）函数的部分图象如图所示.‎ ‎（Ⅰ）写出的最小正周期及图中、的值；‎ ‎（Ⅱ）求在区间上的最大值和最小值.‎ ‎ ‎ ‎（17）（本小题14分）如图，在三棱柱中，侧棱垂直于底面，，，‎ ‎、分别为、的中点.‎ ‎（Ⅰ）求证：平面平面；‎ ‎（Ⅱ）求证：平面；‎ ‎（Ⅲ）求三棱锥的体积.‎ ‎（18）（本小题14分）从某校随机抽取100名学生，获得了他们一周课外阅读时间（单位：小时）的数据，整理得到数据分组及频数分布表和频率分布直方图：‎ 组号 分组 频数 ‎1‎ ‎6‎ ‎2‎ ‎8‎ ‎3‎ ‎17‎ ‎4‎ ‎22‎ ‎5‎ ‎25‎ ‎6‎ ‎12‎ ‎7‎ ‎6‎ ‎8‎ ‎2‎ ‎9‎ ‎2‎ 合计 ‎100‎ ‎ ‎ ‎ ‎ ‎（Ⅰ）从该校随机选取一名学生，试估计这名学生该周课外阅读时间少于12小时的概率；‎ ‎（Ⅱ）求频率分布直方图中的a，b的值；‎ ‎（Ⅲ）假设同一组中的每个数据可用该组区间的中点值代替，试估计样本中的100名学生该周课外阅读时间的平均数在第几组（只需写出结论）‎ ‎（19）（本小题14分）已知椭圆C：.（Ⅰ）求椭圆C的离心率；‎ ‎（Ⅱ）设O为原点，若点A在直线，点B在椭圆C上，且，求线段AB长度的最小值.‎ ‎（20）（本小题13分）已知函数.‎ ‎（Ⅰ）求在区间上的最大值；‎ ‎（Ⅱ）若过点存在3条直线与曲线相切，求t的取值范围；‎ ‎（Ⅲ）问过点分别存在几条直线与曲线相切？（只需写出结论）‎ 绝密★考试结束前 ‎ ‎2014年普通高等学校招生全国统一考试 数学（文）（北京卷）参考答案 一、选择题（共8小题，每小题5分，共40分）‎ ‎（1）C （2）B （3）A （4）C ‎ ‎（5）D （6）C （7）B （8）B 二、填空题（共6小题，每小题5分，共30分）‎ ‎（9）2 （10） （11） ‎ ‎（12） （13）1 （14）42‎ 三、解答题（共6小题，共80分）‎ ‎（15）（共13分）‎ 解：（Ⅰ） 设等差数列的公差为，由题意得 所以．‎ 设等比数列的公比为，‎ 由题意得，解得．‎ 所以．‎ 从而 ‎（Ⅱ）由⑴知．‎ 数列的前项和为，数列的前项和为．‎ 所以，数列的前项和为．‎ ‎（16）（共13分）解：（Ⅰ） 的最小正周期为 ．‎ ‎（Ⅱ） 因为，所以．‎ 于是当，即时，取得最大值0；‎ 当，即时，取得最小值．‎ ‎（17）（共14分）解：（Ⅰ）在三棱柱中，底面．‎ 所以．‎ 又因为．‎ 所以平面．‎ 所以平面平面．‎ ‎（Ⅱ）取中点，连结，．‎ 因为，分别是，的中点，‎ 所以，且．‎ 因为，且，‎ 所以，且．‎ 所以四边形为平行四边形．‎ 所以．‎ 又因为平面，平面，‎ 所以平面．‎ ‎（Ⅲ）因为，，，‎ 所以．‎ 所以三棱锥的体积 ‎．‎ ‎（18）（共13分）解：（Ⅰ）根据频数分布表，100名学生中课外阅读时间不少于12小时的学生共有名，所以样本中的学生课外阅读时间少于12小时的频率是 ‎．‎ 从该校随机选取一名学生，估计其课外阅读时间少于12小时的概率为．‎ ‎（Ⅱ）课外阅读时间落在组的有17人，频率为，所以 ‎．‎ 课外阅读时间落在组的有25人，频率为，‎ 所以．‎ ‎（Ⅲ）样本中的100名学生课外阅读时间的平均数在第4组．‎ ‎（19）（共14分）解：（Ⅰ）由题意，椭圆的标准方程为．‎ 所以，，从而．‎ 因此，．‎ 故椭圆的离心率．‎ ‎（Ⅱ）设点，的坐标分别为，，其中．‎ 因为，‎ 所以，‎ 即，解得．‎ 又，所以 ‎．‎ 因为，且当时等号成立，所以．‎ 故线段长度的最小值为．‎ ‎（20）（共13分）解：（Ⅰ） 由得.‎ 令，得或.‎ 因为，， ‎ 所以 在区间上的最大值为 .‎ ‎（Ⅱ） 设过点的直线与曲线相切于点 ‎ 则且切线斜率为 ‎ 所以切线方程为，‎ 因此 .‎ 整理得.‎ 设 ‎ 则“过点存在3条直线与曲线相切”等价于“有3个不同零点”.‎ ‎.‎ 与的情况如下：‎ ‎0‎ ‎1‎ ‎0‎ ‎0‎ ‎↗‎ ‎↘‎ ‎↗‎ ‎ ‎ 所以，是的极大值，是的极小值．‎ 当，即时，此时在区间和上分别至多有1个零点，所以 至多有2个零点．‎ 当，即时，此时在区间和上分别至多有1个零点，所以 至多有2个零点．‎ 当且，即时，因为，所以 分别在区间，和上恰有个零点.由于在区间和上单调，所以分别在区间和上恰有1个零点.‎ 综上可知，当过点存在条直线与曲线相切时，的取值范围是 .‎ ‎（Ⅲ） 过点 存在条直线与曲线相切；‎ 过点 存在条直线与曲线相切；‎ 过点 存在条直线与曲线相切.：‎