广东省广州市天河中学高考数学理科一轮复习基础知识检测立体几何向量方法——位置关系的证明doc 8页

立体几何中向量方法(一)——位置关系的证明 ‎　　　　　　　　　　　　　　　　　　　‎ ‎1．直线l1，l2相互平行，则下列向量可能是这两条直线的方向向量的是(　　)‎ A．s1＝(0,1,2)，s2＝(2,1,0)‎ B．s1＝(0,1,1)，s2＝(1,1,0)‎ C．s1＝(1,1,2)，s2＝(2,2,4)‎ D．s1＝(1,1,1)，s2＝(－1,2，－1)‎ ‎2．直线l1，l2相互垂直，则下列向量可能是这两条直线的方向向量的是(　　)‎ A．s1＝(1,1,2)，s2＝(2，－1,0)‎ B．s1＝(0,1，－1)，s2＝(2,0,0)‎ ‎ C．s1＝(1,1,1)，s2＝(2,2，－2)‎ D．s1＝(1，－1,1)，s2＝(－2,2，－2)‎ ‎3．若直线l∥平面α，直线l的方向向量为s，平面α的法向量为n，则下列结论正确的是(　　)‎ A．s＝(－1,0,2)，n＝(1,0，－1)‎ B．s＝(－1,0,1)，n＝(1,2，－1)‎ C．s＝(－1,1,1)，n＝(1,2，－1)‎ D．s＝(－1,1,1)，n＝(－2,2,2)‎ ‎4．若直线l⊥平面α，直线l的方向向量为s，平面α的法向量为n，则下列结论正确的是(　　)‎ A．s＝(1,0,1)，n＝(1,0，－1)‎ B．s＝(1,1,1)，n＝(1,1，－2)‎ C．s＝(2,1,1)，n＝(－4，－2，－2)‎ D．s＝(1,3,1)，n＝(2,0，－1)‎ ‎5．若平面α，β平行，则下面可以是这两个平面的法向量的是(　　)‎ A．n1＝(1,2,3)，n2＝(－3,2,1)‎ B．n1＝(1,2,2)，n2＝(－2,2,1)‎ C．n1＝(1,1,1)，n2＝(－2,2,1)‎ D．n1＝(1,1,1)，n2＝(－2，－2，－2)‎ ‎6．若平面α，β垂直，则下面可以是这两个平面的法向量的是(　　)‎ A．n1＝(1,2,1)，n2＝(－3,1,1)‎ B．n1＝(1,1,2)，n2＝(－2,1,1)‎ C．n1＝(1,1,1)，n2＝(－1,2,1)‎ D．n1＝(1,2,1)，n2＝(0，－2，－2)‎ ‎7．直线l的方向向量为s＝(－1,1,1)，平面π的法向量为n＝(2，x2＋x，－x)，若直线l∥平面π，则x的值为(　　)‎ A．－2 B．－ C. 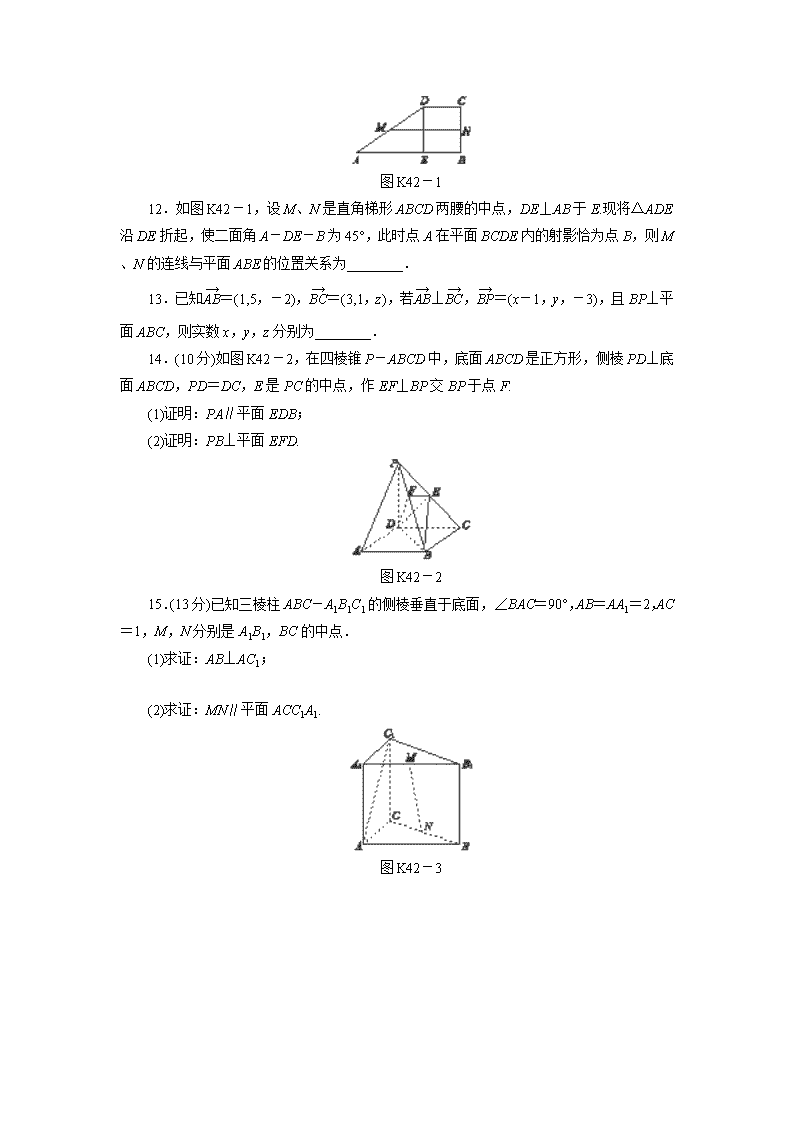D．± ‎8．已知A(1,0,0)，B(0,1,0)，C(0,0,1)，则平面ABC的单位法向量是(　　)‎ A．s＝±(1,1,1) B．s＝± C．s＝± D．s＝± ‎9．已知非零向量a，b及平面α，若向量a是平面α的法向量，则a·b＝0是向量b所在直线平行于平面α或在平面α内的(　　)‎ A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 ‎10．平面α的一个法向量n＝(0,1，－1)，如果直线l⊥平面α，则直线l的单位方向向量是s＝________.‎ ‎11．空间中两个有一条公共边AD的正方形ABCD与ADEF，设M，N分别是BD，AE的中点，给出如下命题：①AD⊥MN；②MN∥平面CDE；③MN∥CE；④MN，CE异面．‎ 则所有正确命题的序号为________．‎ 图K42－1‎ ‎12．如图K42－1，设M、N是直角梯形ABCD两腰的中点，DE⊥AB于E.现将△ADE沿DE折起，使二面角A－DE－B为45°，此时点A在平面BCDE内的射影恰为点B，则M、N的连线与平面ABE的位置关系为________．‎ ‎13．已知＝(1,5，－2)，＝(3,1，z)，若⊥，＝(x－1，y，－3)，且BP⊥平面ABC，则实数x，y，z分别为________．‎ ‎14．(10分)如图K42－2，在四棱锥P－ABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD，PD＝DC，E是PC的中点，作EF⊥BP交BP于点F.‎ ‎(1)证明：PA∥平面EDB；‎ ‎(2)证明：PB⊥平面EFD.‎ 图K42－2‎ ‎15．(13分)已知三棱柱ABC－A1B1C1的侧棱垂直于底面，∠BAC＝90°，AB＝AA1＝2，AC＝1，M，N分别是A1B1，BC的中点．‎ ‎(1)求证：AB⊥AC1；‎ ‎ ‎ ‎(2)求证：MN∥平面ACC1A1.‎ 图K42－3‎ ‎16．(12分)如图K42－4，平面PAC⊥平面ABC，△ABC是以AC为斜边的等腰直角三角形，E，F，O分别为PA，PB，AC的中点，AC＝16，PA＝PC＝10.‎ ‎(1)设G是OC的中点，证明：FG∥平面BOE；‎ ‎(2)是否在△ABO内存在一点M，使FM⊥平面BOE，若存在，求出M的坐标，若不存在，说明理由．‎ 图K42－4‎ 答案解析 ‎【基础热身】‎ ‎1．C　[解析] 两直线平行则其方向向量平行，根据两向量平行的条件检验知正确选项为C.‎ ‎2．B　[解析] 两直线垂直，其方向向量垂直，只有选项B中的两个向量垂直．‎ ‎3．C　[解析] 直线与平面平行，直线的方向向量和平面的法向量垂直，检验知正确选项为C.‎ ‎4．C　[解析] 线面垂直时，直线的方向向量平行于平面的法向量，只有选项C中的两向量平行．‎ ‎【能力提升】‎ ‎5．D　[解析] 两个平面平行时其法向量也平行，检验知正确选项为D.‎ ‎6．A　[解析] 两个平面垂直时其法向量垂直，只有选项A中的两个向量垂直．‎ ‎7．D　[解析] 线面平行时，直线的方向向量垂直于平面的法向量，故x2－2＝0，解得x＝±.‎ ‎8．C　[解析] 先求出平面ABC的一个法向量，再把其单位化．不难求出其一个法向量是n＝(1,1,1)，单位化得s＝±.‎ ‎9．C　[解析] 根据向量与平面平行、以及平面的法向量与直线的方向向量之间的关系进行判断．‎ a·b＝0说明向量b垂直于平面α的法向量，故向量b与平面α共面，此时向量b所在的直线平行于平面α或在平面α之内；反之a·b＝0.‎ ‎10．±　[解析] 直线l的方向向量平行于平面α的法向量，故直线l的单位方向向量是s＝±.‎ ‎11．①②③　[解析] 如图，设＝a，＝b，＝c，‎ 则|a|＝|c|且a·b＝c·b＝0.＝－＝(b＋c)－(a＋b)＝(c－a)，·＝(c－a)·b＝(c·b－a·b)＝0，故AD⊥MN；＝c－a＝2，故MN∥CE，故MN∥平面CDE，故①②③正确；④一定不正确．‎ ‎12．平行　[解析] 由AE⊥DE，BE⊥DE，则∠AEB是二面角A－DE－B的平面角，即∠AEB＝45°，又AB⊥平面BCDE，所以AB＝BE.以B为坐标原点，分别以BC，BE，BA为x轴、y轴、z轴建立空间直角坐标系，‎ 设AB＝BE＝a，BC＝b，则 A(0,0，a)，E(0，a,0)，M，N，‎ ‎∴＝，＝(0，a,0)，＝(0,0，a)，‎ 由此，得＝－－，从而MN∥平面ABE.‎ ‎13.，－，4　[解析] 由题知：⊥，⊥.‎ 所以 即 解得x＝，y＝－，z＝4.‎ ‎14．[解答] 证明：以D为坐标原点，射线DA，DC，DP分别为x，y，z轴的正方向建立空间直角坐标系．设DC＝a.‎ ‎(1)连接AC，AC交BD于G，连接EG.依题意得A(a,0,0)，P(0,0，a)，E.‎ 因为底面ABCD是正方形，所以G是此正方形的中心，故点G的坐标为，‎ 且＝(a,0，－a)，＝.所以＝2，这表明PA∥EG.而EG⊂平面EDB且PA⊄平面EDB，所以PA∥平面EDB.‎ ‎(2)依题意得B(a，a,0)，＝(a，a，－a)．‎ ＝，故·＝0＋－＝0，所以PB⊥DE，‎ ‎ 由已知EF⊥PB，且EF∩DE＝E，所以PB⊥平面EFD.‎ ‎15．[解答] 依条件可知AB，AC，AA1两两垂直．如图，以点A为原点建立空间直角坐标系A－xyz.‎ 根据条件容易求出如下各点坐标：‎ A(0,0,0)，B(0,2,0)，C(－1,0,0)，A1(0,0,2)，B1(0,2,2)，C1(－1,0,2)，M(0,1,2)，N.‎ ‎(1)证明：因为＝(0,2,0)，＝(－1,0,2)，所以·＝0×(－1)＋2×0＋0×2＝0.‎ 所以⊥，即AB⊥AC1.‎ ‎(2)证明：因为＝，＝(0,2,0)是平面ACC1A1的一个法向量，‎ 且·＝－×0＋0×2－2×0＝0，‎ 所以⊥.‎ 又MN⊄平面ACC1A1，‎ 所以MN∥平面ACC1A1.‎ ‎【难点突破】‎ ‎16．[解答] (1)证明：如图，连接OP，以O为坐标原点，分别以OB、OC、OP所在直线为x轴，y轴，z轴，建立空间直角坐标系O－xyz，‎ 则O(0,0,0)，A(0，－8,0)，B(8,0,0)，C(0,8,0)，P(0,0,6)，E(0，－4,3)，F(4,0,3)，由题意得，G(0,4,0)，则＝(8,0,0)，＝(0，－4,3)，因此可得平面BOE的一个法向量为n ‎＝(0,3,4)，＝(－4,4，－3)，得n·＝0，又直线FG不在平面BOE内，因此有FG∥平面BOE.‎ ‎(2)设点M的坐标为(x0，y0,0)，则＝(x0－4，y0，－3)，因为FM⊥平面BOE，所以有∥n，因此有x0＝4，y0＝－，即点M的坐标为，在平面xOy中，△AOB的内部区域满足不等式组经检验，点M的坐标满足上述不等式组，所以在△ABO内存在一点M，使FM⊥平面BOE.‎