三角函数与三角形高考十年高考数学全国卷文 12页

三角函数与三角形（全国卷1）‎ 一．基础题组 ‎1. 【2014全国1，文2】若，则( )‎ A. B. C. D. ‎ ‎2. 【2012全国1，文3】若函数(φ∈0,2π])是偶函数，则φ＝(　　) ,‎ A． B． C． D．‎ ‎3. 【2010全国1，文1】cos300°等于(　　)‎ A．－　　 　B．－ C. 　　　　D. ‎ ‎4. 【2009全国卷Ⅰ,文1】sin585°的值为( )‎ A. B. C. D.‎ ‎5. 【2008全国1，文6】是（ ）‎ A．最小正周期为的偶函数 B．最小正周期为的奇函数 C．最小正周期为的偶函数 D．最小正周期为的奇函数 ‎6. 【2007全国1，文2】是第四象限角，，则（ ）‎ A. B. C. D.‎ ‎7.【2016新课标1文数】△ABC的内角A、B、C的对边分别为a、b、c.已知，，，则b=( )‎ ‎（A） （B） （C）2 （D）3‎ ‎8. 【2016新课标1文数】将函数y=2sin (2x+)的图像向右平移个周期后，所得图像对应的函数为 ‎（A）y=2sin(2x+) （B）y=2sin(2x+) （C）y=2sin(2x–) （D）y=2sin(2x–)‎ ‎9. 【2011新课标，文15】中,则的面积为 .‎ ‎10. 【2011全国1，文14】Z+xx, ‎ 12‎ ‎11. 【2010全国1，文14】已知α为第二象限的角，sinα＝，则tan2α＝__________.‎ ‎12.【2017新课标1，文15】已知，tan α=2，则=__________．‎ ‎13.【2016新课标1文数】已知θ是第四象限角，且sin(θ+)=，则tan(θ–)= .‎ 二．能力题组 ‎1. 【2014全国1，文7】在函数①，② ，③,④中，最小正周期为的所有函数为( )‎ A.①②③ B. ①③④ C. ②④ D. ①③‎ ‎2. 【2013课标全国Ⅰ，文10】已知锐角△ABC的内角A，B，C的对边分别为a，b，c,23cos2A＋cos 2A＝0，a＝7，c＝6，则b＝(　　)‎ A．10 B．9 C．8 D．5‎ ‎3. 【2005全国1，文6】当时，函数的最小值为(　　)‎ ‎（A）2 （B） （C）4 （D）‎ ‎4. 【2011全国1，文7】设函数，将的图像向右平移个单位长度后，所得的图像与原图像重合，则的最小值等于（ ）Z.X.X.‎ ‎（A） （B） （C） （D）‎ ‎6. 【2009全国卷Ⅰ,文10】如果函数y=3cos(2x+φ)的图像关于点(,0)中心对称,那么|φ|的最小值为( )‎ A. B. C. D.‎ ‎7. 【2008全国1，文9】为得到函数的图象，只需将函数的图像（ ）‎ A．向左平移个长度单位 B．向右平移个长度单位 C．向左平移个长度单位 D．向右平移个长度单位 ‎8. 【2007全国1，文10】函数的一个单调增区间是（ ）‎ A. B. C. D.‎ ‎8. 【2012全国1，文4】已知α为第二象限角，，则sin2α＝(　　)‎ A． B． C． D．‎ 12‎ ‎9. 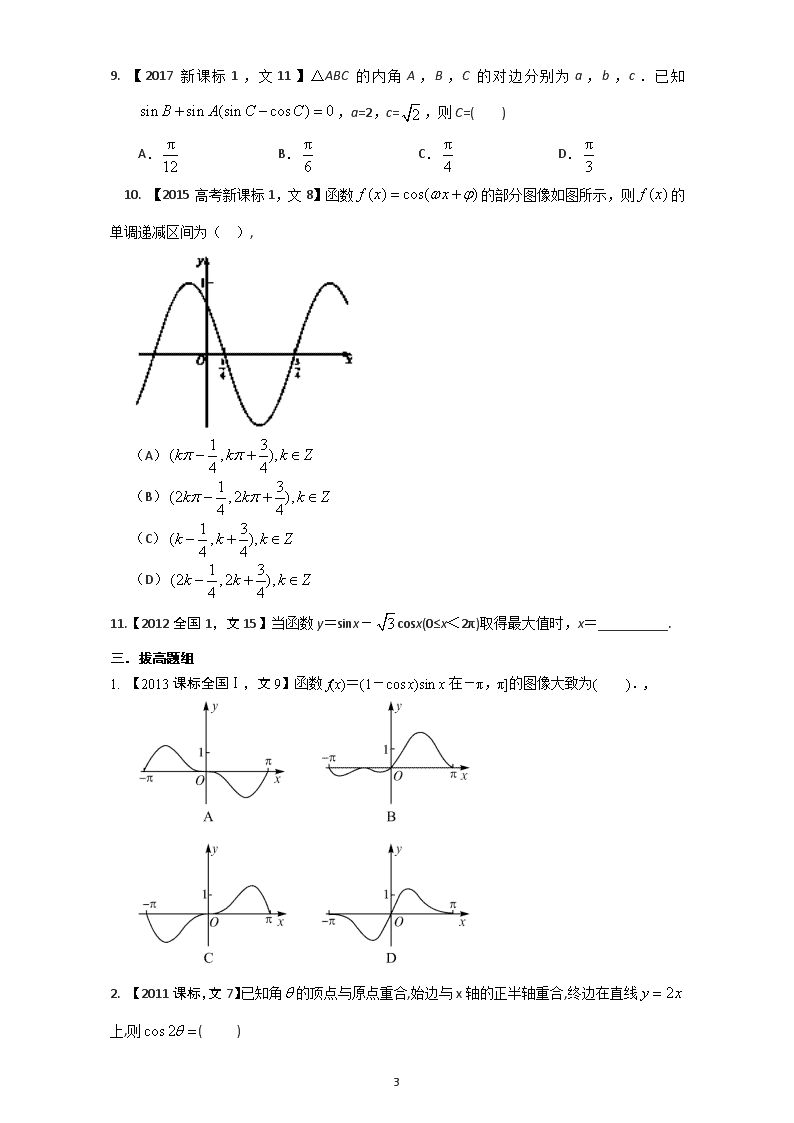【2017新课标1，文11】△ABC的内角A，B，C的对边分别为a，b，c．已知，a=2，c=，则C=(　　)‎ A． B． C． D．‎ ‎10. 【2015高考新课标1，文8】函数的部分图像如图所示，则的单调递减区间为（ ）, ‎ ‎ （A） ‎ ‎（B）‎ ‎（C）‎ ‎（D）‎ ‎11.【2012全国1，文15】当函数y＝sinx－cosx(0≤x＜2π)取得最大值时，x＝__________.‎ 三．拔高题组 ‎1. 【2013课标全国Ⅰ，文9】函数f(x)＝(1－cos x)sin x在－π，π]的图像大致为(　　)．,‎ ‎2. 【2011课标，文7】已知角的顶点与原点重合,始边与x轴的正半轴重合,终边在直线上,则( )‎ 12‎ A. B. C. D.‎ ‎3. 【2011课标，文11】‎ ‎4.【2014全国1，文16】如图，为测量山高，选择和另一座山的山顶为测量观测点.从点测得 点的仰角，点的仰角以及；从点测得.已知山高，则山高________‎ ‎5. 【2013课标全国Ⅰ，文16】设当x＝θ时，函数f(x)＝sin x－2cos x取得最大值，则cos θ＝______.‎ ‎6. 【2012全国1，文17】△ABC中，内角A，B，C成等差数列，其对边a，b，c满足2b2＝3ac，求A．‎ 12‎ ‎7. 【2005全国1，文17】‎ 设函数图像的一条对称轴是直线。‎ ‎（Ⅰ）求；‎ ‎（Ⅱ）求函数的单调增区间；‎ ‎（Ⅲ）画出函数在区间上的图像。‎ ‎8. 【2011全国1，文18】△ABC的内角A、B、C的对边分别为a、b、c.己知 ‎ (Ⅰ)求B；‎ ‎（Ⅱ）若 12‎ ‎9. 【2009全国卷Ⅰ,文18】在△ABC中,内角A、B、C的对边长分别为a、b、c.已知a2-c2=2b,且sinB=4cosAsinC,求b. ,‎ ‎10. 【2007全国1，文17】设锐角三角形ABC的内角A，B，C的对边分别为a，b，c，a=2bsinA。‎ ‎（Ⅰ）求B的大小；‎ ‎（Ⅱ）若，，求b。‎ ‎11. 【2015高考新课标1，文17】已知分别是内角的对边，.‎ ‎（I）若，求 ‎ ‎（II）若，且 求的面积.‎ 12‎ ‎12. 【2008全国1，文17】‎ 设的内角所对的边长分别为，且，．‎ ‎（Ⅰ）求边长；‎ ‎（Ⅱ）若的面积，求的周长．‎ 全国卷2‎ 一．基础题 ‎1. 【2016新课标2文数】函数 的部分图像如图所示，则 ‎（A） （B）‎ ‎（C） （D）‎ ‎2. 【2017新课标2，文3】函数的最小正周期为 A． B． C． D． ‎ ‎3.【2016新课标2文数】函数的最大值为 ‎（A）4 （B）5 （C）6 （D）7‎ 12‎ ‎4. 【2013课标全国Ⅱ，文4】△ABC的内角A，B，C的对边分别为a，b，c，已知b＝2，，，则△ABC的面积为(　　)．‎ A． B． C． D．‎ ‎5. 【2010全国2，文3】已知sinα＝，则cos(π－2α)等于(　　)‎ A．－ B．－ C. D. ‎ ‎6. 【2007全国2，文1】cos330°=( )‎ ‎(A) (B) (C) (D) ‎ ‎7. 【2007全国2，文3】函数f(x)=|sinx|的一个单调递增区间是( )‎ ‎(A)（，） (B) （，） (C) （，） (D) （，2）‎ ‎8. 【2006全国2，文3】函数的最小正周期是( )‎ ‎（A）　　　　（B）　　　　（C）　　　　（D）‎ ‎9. 【2005全国3，文1】已知为第三象限角，则所在的象限是（ ） ‎ A．第一或第二象限 B．第二或第三象限 C．第一或第三象限 D．第二或第四象限 ‎10. 【2005全国2，文1】函数的最小正周期是（ ）‎ ‎(A) (B) (C) (D) ‎ ‎11. 【2005全国2，文4】已知函数在内是减函数，则（ ）‎ ‎(A) (B) (C) (D) ‎ ‎14.【2014全国2，文14】 函数的最大值为________．‎ ‎15. 【2010全国2，文13】已知α是第二象限的角，tanα＝，则cosα＝________.‎ 二．能力题组 ‎1. 【2013课标全国Ⅱ，文6】已知sin 2α＝，则＝(　　)．‎ A． B． C． D．‎ 12‎ ‎2. 【2012全国新课标，文9】已知ω＞0,0＜φ＜π，直线和是函数f(x)＝sin(ωx＋φ)图像的两条相邻的对称轴，则φ＝(　　)‎ A． B． C． D．‎ ‎3. 【2010全国新课标，文10】若cosα＝－，α是第三象限的角，则sin(α＋)等于 (　　)‎ A．－ B. C．－ D.‎ ‎4. 【2005全国3，文7】设,且,则 （ ）‎ ‎ A． B． C． D．‎ ‎5. 【2010全国新课标，文16】在△ABC中，D为BC边上一点，BC＝3BD，AD＝，∠ADB＝135°.若AC＝AB，则BD＝________.‎ ‎6. 【2016新课标2文数】△ABC的内角A，B，C的对边分别为a，b，c，若，，a=1，则b=____________.‎ ‎7.【2017新课标2，文13】函数的最大值为 . ‎ ‎8.【2017新课标2，文16】的内角的对边分别为,若,则 .‎ 三．拔高题组 ‎1. 【2005全国3，文8】 = （ ）‎ ‎ A． B． C．1 D．‎ ‎2. 【2013课标全国Ⅱ，文16】函数y＝cos(2x＋φ)(－π≤φ＜π)的图像向右平移个单位后，与函数y＝的图像重合，则φ＝__________.‎ ‎3.【2015新课标2文数】△ABC中D是BC上的点,AD平分BAC,BD=2DC.‎ ‎（I）求 ；‎ ‎（II）若,求.‎ 12‎ ‎4. 【2014全国2，文17】 四边形的内角与互补，.‎ ‎ （Ⅰ）求和；‎ ‎ （Ⅱ）求四边形的面积.‎ ‎5. 【2012全国新课标，文17】已知a，b，c分别为△ABC三个内角A，B，C的对边，acosC＋asinC－b－c＝0．‎ ‎(1)求A；‎ ‎(2)若a＝2，△ABC的面积为，求b，c．‎ ‎6. 【2006全国2，文17】‎ 在,求 ‎（1）‎ ‎（2）若点 12‎ ‎7. 【2005全国3，文17】‎ 已知函数求使为正值的的集合.‎ 9. ‎【2005全国2，文17】‎ 已知为第二象限的角，，为第一象限的角，．求的值．‎ ‎10. 【2010全国2，文17】△ABC中，D为边BC上的一点，BD＝33，sinB＝，cos∠ADC＝，求AD.‎ ‎7. 【2007全国2，文18】 ‎ 在 ∆ABC中，已知内角A=,边 BC=2,设内角B=x, 周长为y ‎（1）求函数y=f(x)的解析式和定义域；‎ ‎（2）求y的最大值 12‎ 12‎