高考总复习天津中学解三角形单元教师全套 12页

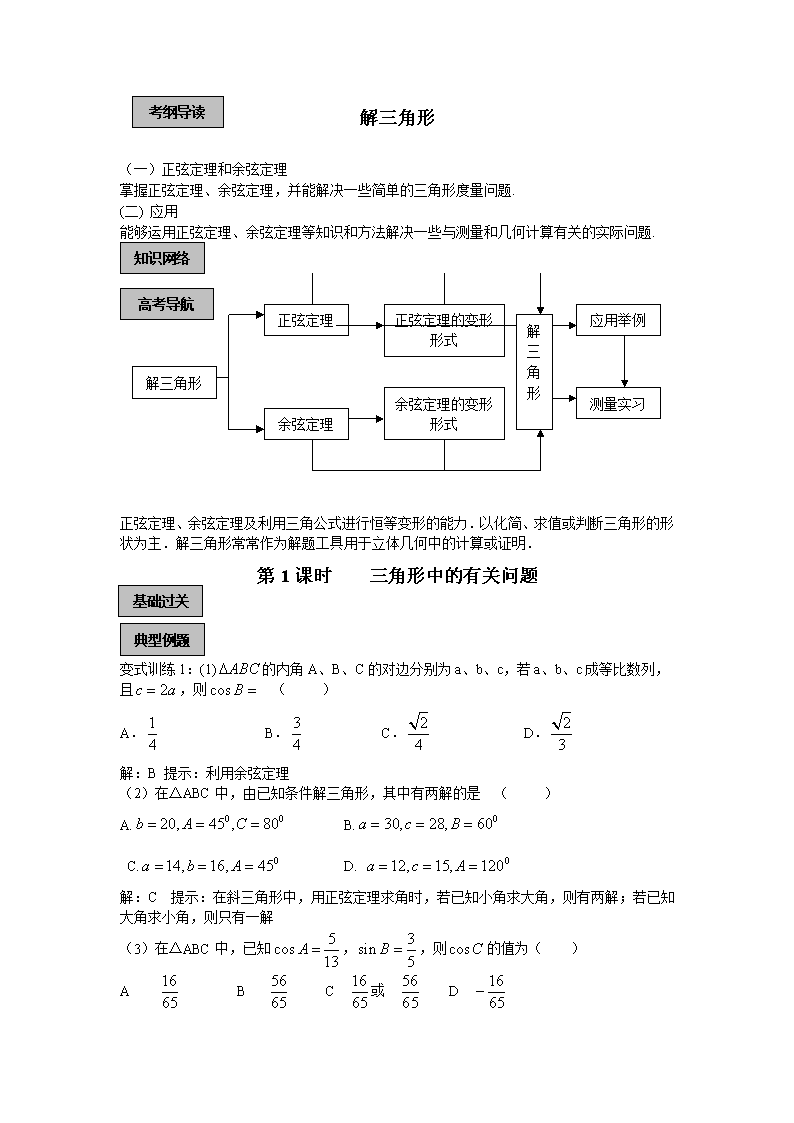
考纲导读 解三角形 ‎（一）正弦定理和余弦定理 掌握正弦定理、余弦定理，并能解决一些简单的三角形度量问题. ‎(二) 应用 能够运用正弦定理、余弦定理等知识和方法解决一些与测量和几何计算有关的实际问题. 知识网络 解三角形 正弦定理 余弦定理 正弦定理的变形形式 余弦定理的变形形式 解三角形 应用举例 测量实习 高考导航 正弦定理、余弦定理及利用三角公式进行恒等变形的能力．以化简、求值或判断三角形的形状为主．解三角形常常作为解题工具用于立体几何中的计算或证明． 基础过关 第1课时 三角形中的有关问题 典型例题 变式训练1：(1)的内角A、B、C的对边分别为a、b、c，若a、b、c成等比数列，且，则 （ ） A． B． C． D． 解：B 提示：利用余弦定理 ‎（2）在△ABC中，由已知条件解三角形，其中有两解的是 （ ） A. B. ‎ C. D. 解：C 提示：在斜三角形中，用正弦定理求角时，若已知小角求大角，则有两解；若已知大角求小角，则只有一解 ‎（3）在△ABC中，已知，，则的值为（ ） A B C 或 D 解：A 提示:在△ABC中，由 知角B为锐角 ‎（4）若钝角三角形三边长为、、，则的取值范围是 ． 解： 提示：由可得 ‎（5）在△ABC中，= ． 解：提示：由面积公式可求得，由余弦定理可求得 ‎ ‎ 例3. 已知在△ABC中，sinA(sinB＋cosB)－sinC＝0，sinB＋cos‎2C＝0，求角A、B、C． 解：由sinA(sinB＋cosB)－sinC＝0，得sinAsinB＋sinAcosB－sin(A＋B)＝0， 所以sinB(sinA－cosA)＝0 ‎∵B∈(0, π), ∴sinB≠0, ∴cosA＝sinA，由A∈(0, π)，知A＝从而B＋C＝，由sinB＋cos‎2C＝0得sinB＋cos2(－B)＝0 cos＝(－2B)＝cos[2π－(＋2B)]＝cos(＋2B)＝－sin2B 得sinB－sin2B＝0，亦即sinB－2sinBcosB＝0，由此各cosB＝，B＝，C＝ ‎∴A＝ B＝ C＝ 变式训练3：已知△ABC中，2（sin‎2A－sin‎2C）=（a－b）sinB，△ABC外接圆半径为. ‎（1）求∠C； ‎（2）求△ABC面积的最大值. 解：（1）由2（sin‎2A－sin‎2C）=（a－b）·sinB得 ‎2（－）=（a－b）. 又∵R=，∴a2－c2=ab－b2.∴a2+b2－c2=ab.∴cosC==. 又∵0°＜C＜180°，∴C=60°. ‎（2）S=absinC=×ab=2sinAsinB=2sinAsin（120°－A） ‎=2sinA（sin120°cosA－cos120°sinA）=3sinAcosA+sin‎2A ‎=sin‎2A－cos‎2A+=sin（‎2A－30°）+. ‎∴当‎2A=120°，即A=60°时，Smax=. ‎ ‎小结归纳 小结归纳 基础过关 第2课时 应用性问题 ‎1．三角形中的有关公式（正弦定理、余弦定理、三角形内角和定理、三角形面积公式等）； ‎２．正弦定理和余弦定理解三角形的常见问题有：测量距离问题、测量高度问题、测量角度问题、计算面积问题、航海问题、物理问题等； ‎３．实际问题中有关术语、名称． ‎（1）仰角和俯角：在目标视线和水平视线所成的角中，目标视线在水平视线上方的角叫仰角；在水平视线下方的角叫俯角 ‎（2）方位角：指正北方向顺时针转到目标方向线水平角． 典型例题 例1．(1)某人朝正东方走km后，向左转1500，然后朝新方向走‎3km，结果它离出发点恰好km，那么等于 （ ） ‎ （A） （B） （C）或 （D）3 解：C 提示：利用余弦定理 ‎（2）甲、乙两楼相距，从乙楼底望甲楼顶的仰角为，从甲楼顶望乙楼顶的俯角为，则甲、乙两楼的高分别是 （ ） A B C D 解：A ‎（3）一只汽球在的高空飞行，汽球上的工件人员测得前方一座山顶上A点处的俯角为，汽球向前飞行了后，又测得A点处的俯角为，则山的高度为（ ）‎ A B C D ‎ 解： B ‎ ‎（4）已知轮船A和轮船B同时离开C岛，A向北偏东方向，B向西偏北方向，若A的航行速度为25 nmi/h，B的速度是A的，过三小时后，A、B的距离是 ．‎ 解：90.8 nmi ‎(5) 货轮在海上以‎40km/h的速度由B到C航行，‎ 航向为方位角，A处有灯塔， ‎ 其方位角，在C处观测灯塔A的 ‎ 方位角，由B到C需航行半小时， ‎ 则C到灯塔A的距离是 ‎ 解：km 提示：由题意知 ，利用余弦定理或解直角三角形可得 变式训练1：如图，当甲船位于A处时获悉，在其正东方向相距‎20海里的B处有一艘渔船遇险等待营救．甲船立即前往救援，同时把消息告知在甲船的南偏西30，相距‎10海里C处的乙船，试问乙船应朝北偏东多少度的方向沿直线前往B处救援（角度精确到1）？‎ 北 ‎20‎ ‎10‎ A B ‎•C 解：连接BC,由余弦定理得BC2=202+102－2×20×10×cos120°=700.‎ ‎ 于是,BC=10.‎ ‎ ∵, ∴sin∠ACB=,‎ ‎ ∵∠ACB<90° ∴∠ACB=41°‎ ‎∴乙船应朝北偏东71°方向沿直线前往B处救援.‎ 例2. 在某海滨城市附近海面有一台风，据检测，当前台风中心位于城市O(如图)的东偏南方向‎300 km的海面P处，并以‎20 km / h的速度向西偏北的方向移动，台风侵袭的范围为圆形区域，当前半径为‎60 km ，并以‎10 km / h的速度不断增加，问几小时后该城市开始受到台风的侵袭？持续多长时间？‎ 解：设在时刻t(h)台风中心为Q,此时台风侵袭的圆形区域半径为10t+60(km)‎ 若在时刻t城市O受到台风的侵袭,则 由余弦定理知 由于PO=300,PQ=20t 故 即 解得 ‎ 答：12小时后该城市受到台风的侵袭，侵袭的时间将持续12小时．‎ 变式训练2：如图所示,海岛A周围‎38海里内有暗礁，一艘船向正南方向航行，在B处测得岛A在船的南偏东方向上，船航行‎30海里后，在C处测得岛A在船的南偏东 方向上，如果此船不改变航向，继续向南航行，有无触礁危险？‎ 解：由题意得，在△ABC中，BC=30，，‎ ‎ 所以 ，由正弦定理可知：‎ ‎ 所以，‎ 于是A到BC所在直线的距离为 所以船继续向南航行无触礁危险。‎ 例3. 如图所示，公园内有一块边长的等边△ABC形状的三角地，‎ 现修成草坪，图中DE把草坪分成面积相等的两部分，D在AB上，‎ E在AC上.‎ ‎（1）设AD，ED，求用表示的函数关系式；‎ ‎（2）如果DE是灌溉水管，为节约成本希望它最短，DE的位置 应该在哪里？如果DE是参观线路，则希望它最长，DE的 位置又在哪里？请给予证明.‎ 解：（1）在△ABC中，D在AB上，‎ S△ADE=S△ABC ‎ ‎ ，在△ADE中，由余弦定理得：‎ ‎ ‎ ‎（2）令 ，则 则 令 ，‎ 则 ‎；‎ 有最小值，此时DE∥BC，且 ‎ 有最大值，此时DE为△ABC ‎ 的边AB或AC的中线上.‎ 变式训练3：水渠道断面为等腰梯形，如图所示，渠道深为，梯形面积为S，为了使渠道的渗水量达到最小，应使梯形两腰及下底之和达到最小，此时下底角应该是多少？‎ 解：设 ，则，‎ ‎ 所以 ‎ 设两腰与下底之和为，‎ 则 ‎ ‎ ‎ ‎ 当且仅当 时，上式取等号，即当时，上式取等号 ‎，所以下角时，梯形两腰及下底之和达到最小．‎ 例4. 如图，半圆O的直径为2，A为直径延长线上的一点，OA=2，B为半圆上任意一点，以AB为一边作等边三角形ABC。问：点B在什么位置时，四边形OACB面积最大？‎ 解：设，在△AOB中，由余弦定理得：‎ ‎ ‎ ‎ ‎ ‎ 于是，四边形OACB的面积为 ‎ S=S△AOB+ S△ABC ‎ ‎ ‎ ‎ 因为，所以当，，即时，‎ 四边形OACB面积最大．‎ 变式训练4：如图所示，某海岛上一观察哨A上午11时测得一轮船在海岛北偏东的C处，12时20分测得船在海岛北偏西的B处，12时40分轮船到达位于海岛正西方且距海岛‎5 km的E港口，如果轮船始终匀速直线前进，问船速多少？‎ 解：轮船从C到B用时80分钟，从B到E用时20分钟， ‎ ‎ 而船始终匀速前进，由此可见：BC=4EB，设EB=，则 ‎ 则BC=4，由已知得 在△AEC中，由正弦定理得：‎ ‎ ‎ 在△ABC中，由正弦定理得：‎ 在△ABE中，由余弦定理得：‎ ‎ 所以船速 答：该船的速度为 km/h 解三角形章节测试题 一、选择题 ‎1．在中，，，，则的面积是（　　）‎ A．　　　　　B．　　　　 C．　　　 　D．‎ ‎2．在中，若，则的值为（　　）‎ A．　　 　　B． 　　　　 C．　　　 D．‎ ‎3．在中，若，则这个三角形中角的值是（　　）‎ A．或　　　B．或　　　C．或　　　D．或 ‎ ‎4．在中，根据下列条件解三角形，其中有两个解的是（　　）‎ A．，，　　　　B．，，　‎ C．，，　　　　 　D．，，　‎ ‎5．已知三角形的两边长分别为4,5，它们夹角的余弦是方程的根，则第三边长是（　　）‎ A．　　　　　B．　　　　 C．　　　 　D． ‎ ‎6．在中，如果，那么角等于（　　）‎ A．　　　　　B．　　　　 C．　　 　D．‎ ‎7．在中，若，，此三角形面积，则的值是（　　）‎ A．　　　　　B．　　　　　C．　　　　 D． ‎ ‎8．在△ABC中，AB=3，BC=，AC=4，则边AC上的高为（ ）‎ A． 　 　B． C． D．‎ ‎9．在中，若，，，则（　　）‎ A．　 　B．‎ ‎ C．　 D．‎ ‎10．如果满足，，的△ABC恰有一个，那么的取值范围是（　　）‎ A． 　B． 　C． 　D．或 二、填空题 ‎11．在中，若，则最大角的余弦值等于_________________．‎ ‎12．在中，，，，则此三角形的最大边的长为____________________．‎ ‎13．在中，已知，，，则__________________．‎ ‎14．在中，，，，则_______________，_______________．‎ 三、解答题 ‎15．△ABC中，D在边BC上，且BD＝2，DC＝1，∠B＝60o，∠ADC＝150o，求AC的长及△ABC的面积．‎ ‎16．在△ABC中，已知角A，B，C的对边分别为a，b，c，且bcosB＋ccosC＝acosA，试判断△ABC的形状．‎ ‎17. 如图，海中有一小岛，周围3.8海里内有暗礁。一军舰从A地出发由西向东航行，望见小岛B在北偏东75°，航行8海里到达C处，望见小岛B在北端东60°。若此舰不改变舰行的方向继续前进，问此舰有没有角礁的危险？‎ ‎18．如图，货轮在海上以35n mile/h的速度沿方位角(‎ 从正北方向顺时针转到目标方向线的水平角)为152o的方向航行．为了确定船位，在B点处观测到灯塔A的方位角为122o．半小时后，货轮到达C点处，观测到灯塔A的方位角为32o．求此时货轮与灯塔之间的距离．‎ A ‎ C ‎ B 北 北 ‎152o ‎32 o ‎122o ‎19. 航空测量组的飞机航线和山顶在同一铅直平面内，已知飞机的高度为海拔‎10000m,速度为‎180km（千米）/h（小时）飞机先看到山顶的俯角为150，经过420s（秒）后又看到山顶的俯角为450，求山顶的海拔高度（取＝1.4,＝1.7）．‎ ‎20．如图所示，a是海面上一条南北方向的海防警戒线，在a上点A处有一个水声监测点，另两个监测点B，C分别在A的正东方‎20 km处和‎54 km处．某时刻，监测点B收到发自静止目标P的一个声波，8s后监测点A，20 s后监测点C相继收到这一信号．在当时气象条件下，声波在水中的传播速度是1. ‎5 km/s.‎ ‎ （1）设A到P的距离为 km，用表示B,C到P 的距离，并求值；‎ ‎ （2）求静止目标P到海防警戒线a的距离（结果精确到‎0.01 km）.‎ 解三角形章节测试参考答案 ‎1．C 2.B 3.D 4.D 5.B 6.B7.D. 8.B ‎9 A 10.D　‎ ‎11． 12、 13、6或3 14、　‎ ‎15．在△ABC中，∠BAD＝150o－60o＝90o，∴AD＝2sin60o＝．‎ 在△ACD中，AD2＝()2＋12－2××1×cos150o＝7，∴AC＝．‎ ‎∴AB＝2cos60o＝1．S△ABC＝×1×3×sin60o＝．‎ ‎16．∵ bcosB＋ccosC＝acosA，由正弦定理得：sinBcosB＋sinCcosC＝sinAcosA，‎ 即sin2B＋sin‎2C＝2sinAcosA，∴2sin(B＋C)cos(B－C)＝2sinAcosA．∵A＋B＋C＝π，‎ ‎∴sin(B＋C)＝sinA．而sinA≠0，∴cos(B－C)＝cosA，即cos(B－C)＋cos(B＋C)＝0，‎ ‎∴2cosBcosC＝0．∵ 0＜B＜π，0＜C＜π，∴B＝或C＝，即△ABC是直角三角形．‎ ‎17、解：过点B作BD⊥AE交AE于D ‎ 由已知，AC=8，∠ABD=75°，∠CBD=60°‎ 在Rt△ABD中，‎ AD=BD·tan∠ABD=BD·tan 75°‎ 在Rt△CBD中，‎ CD=BD·tan∠CBD=BD·tan60°‎ ‎∴AD－CD=BD（tan75°－tan60°）=AC=8,…9分 ‎∴‎ ‎∴该军舰没有触礁的危险。‎ ‎18．在△ABC中，∠B＝152o－122o＝30o，∠C＝180o－152o＋32o＝60o，∠A＝180o－30o－60o＝90o，BC＝，∴AC＝sin30o＝．‎ 答：船与灯塔间的距离为n mile．‎ ‎19. 解：如图 ∵150　450　　　‎ ‎∴300， ‎ AB= ‎180km（千米）/h（小时）420s（秒）‎ ‎= 21000(m ) ‎ ‎∴在中 ‎∴ ‎ ‎∴‎ ‎∵， ‎ ‎∴‎ ‎　　　＝‎ ‎　　　＝＝‎ ‎　　　＝7350‎ 山顶的海拔高度＝10000-7350=2650(米) ‎ ‎20．解：(1)依题意，PA－PB=1. 5 × 8=12 (km)，PC－PB=1.5×20=30（km ）．‎ 因此 PB＝（x一12）km，PC=（18＋x）km. ‎ 在△PAB中，AB= ‎20 km，‎ ‎ ‎ 同理，在△PAC中， ‎ 由于 即 解得（km）． ‎ ‎ (2)作PDa,垂足为D. 在Rt△PDA中，‎ PD =PAcos∠APD=PAcos∠PAB = （km）．‎ 答：静止目标P到海防警戒线a的距离约为17. ‎71 km. ‎ ‎ ‎