立体几何高考题文科 4页

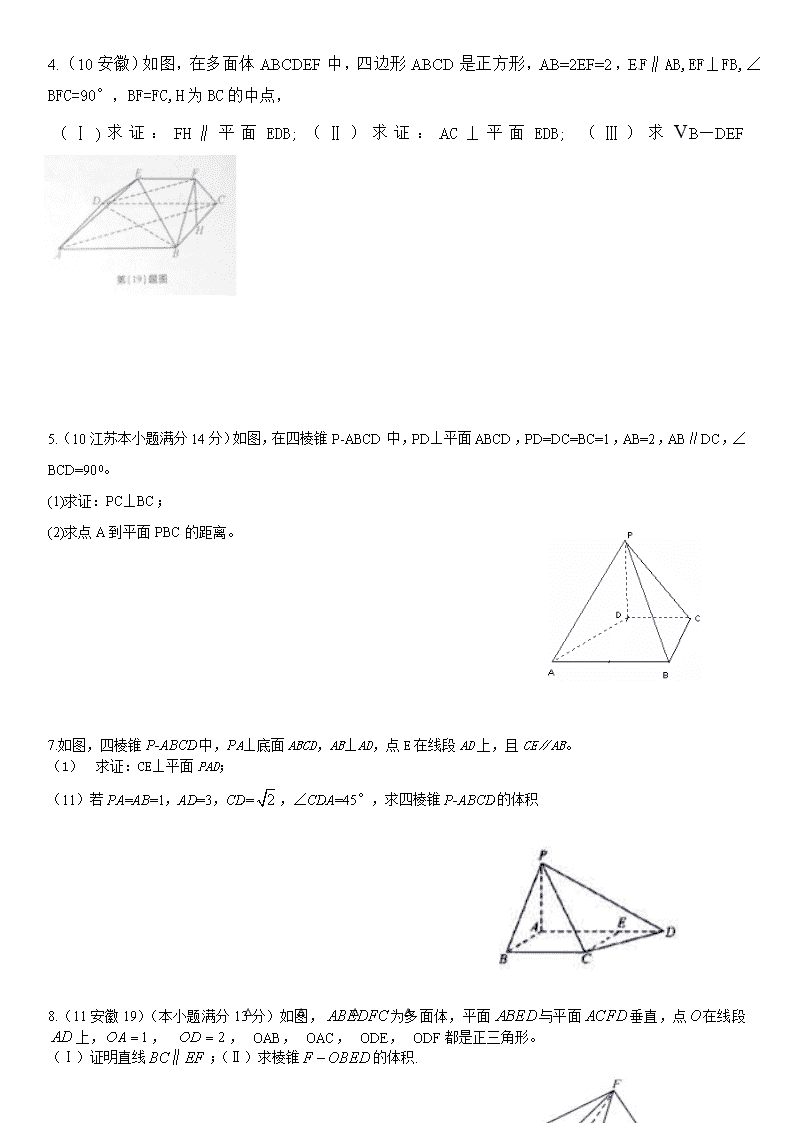
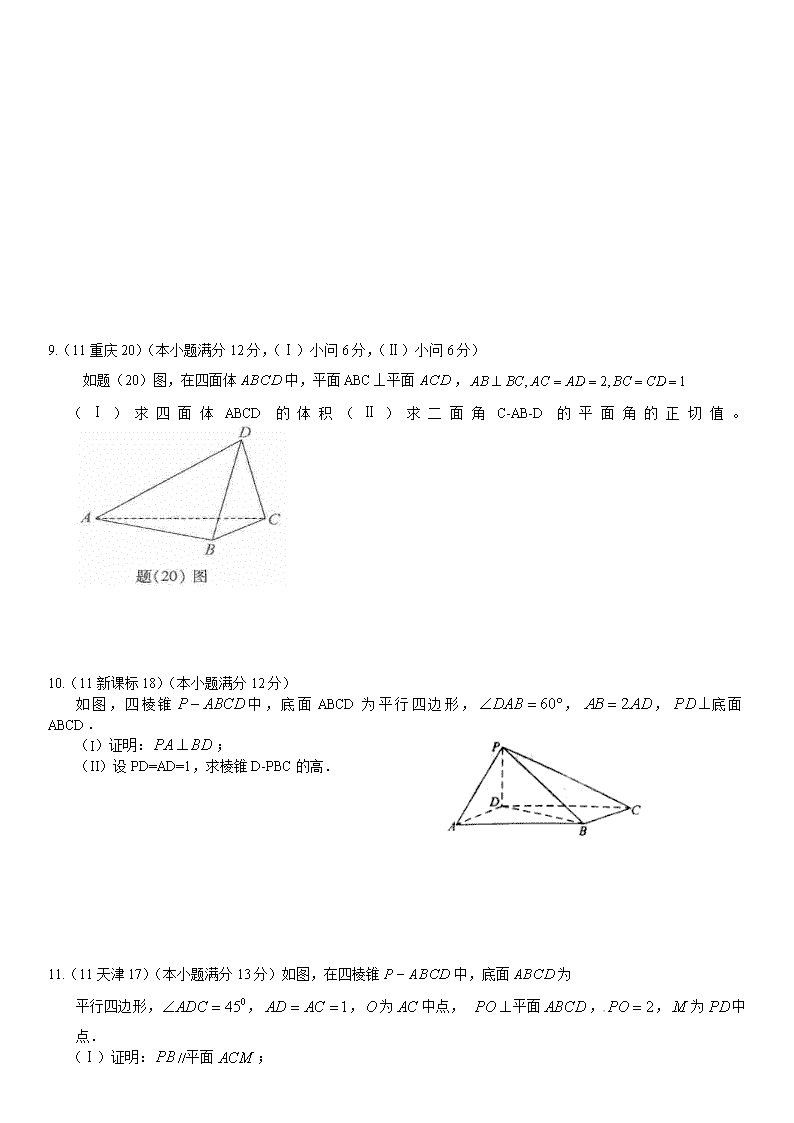
‎4.（10安徽）如图，在多面体ABCDEF中，四边形ABCD是正方形，AB=2EF=2，EF∥AB,EF⊥FB,∠BFC=90°，BF=FC,H为BC的中点，‎ ‎(Ⅰ)求证：FH∥平面EDB;（Ⅱ）求证：AC⊥平面EDB; （Ⅲ）求VB—DEF ‎ ‎5.（10江苏本小题满分14分）如图，在四棱锥P-ABCD中，PD⊥平面ABCD，PD=DC=BC=1，AB=2，AB∥DC，∠BCD=900。‎ (1) 求证：PC⊥BC；‎ (2) 求点A到平面PBC的距离。‎ ‎7.如图，四棱锥P-ABCD中，PA⊥底面ABCD，AB⊥AD，点E在线段AD上，且CE∥AB。‎ （1） 求证：CE⊥平面PAD；‎ ‎（11）若PA=AB=1，AD=3，CD=，∠CDA=45°，求四棱锥P-ABCD的体积 ‎8.（11安徽19）（本小题满分13分） 如图，为多面体，平面与平面垂直，点在线段上，，，△OAB，△OAC，△ODE，△ODF都是正三角形。‎ ‎（Ⅰ）证明直线；（Ⅱ）求棱锥的体积.‎ ‎9.（11重庆20）（本小题满分12分，（Ⅰ）小问6分，（Ⅱ）小问6分）‎ ‎ 如题（20）图，在四面体中，平面ABC⊥平面，‎ ‎ （Ⅰ）求四面体ABCD的体积（Ⅱ）求二面角C-AB-D的平面角的正切值。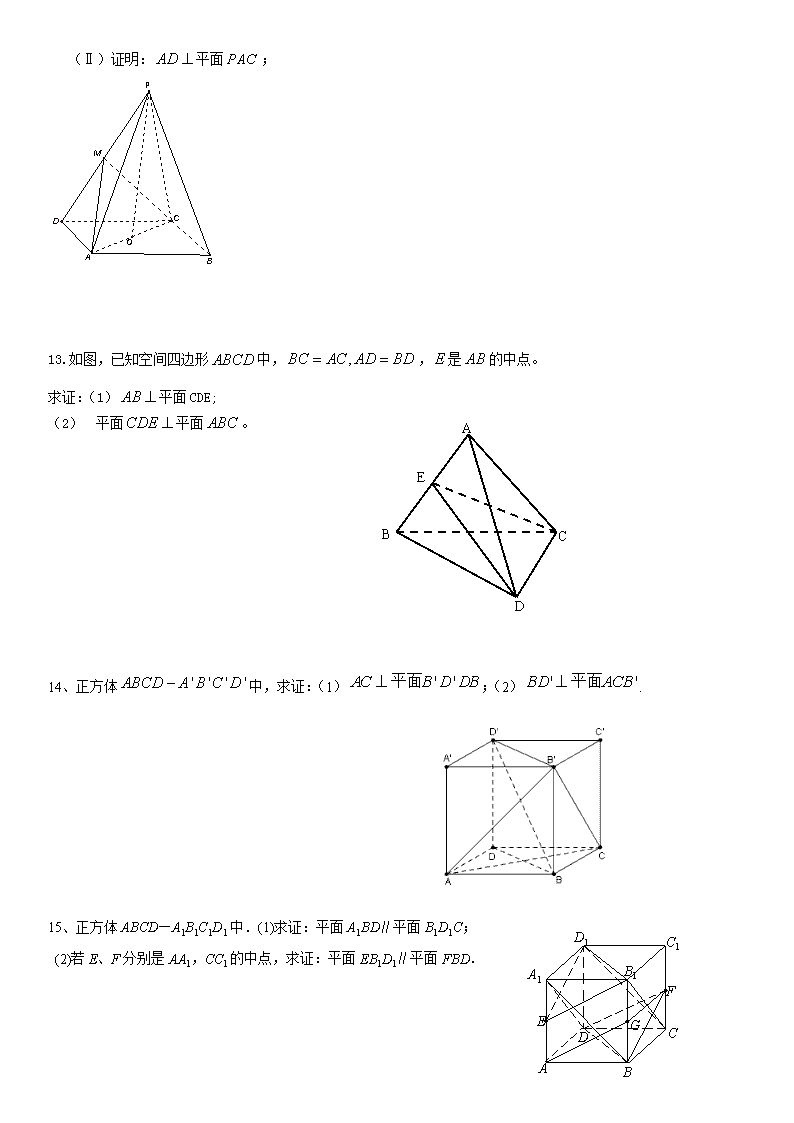 ‎ ‎ ‎ ‎10.（11新课标18）（本小题满分12分）‎ 如图，四棱锥中，底面ABCD为平行四边形，，，底面ABCD．‎ ‎ （I）证明：；‎ ‎ （II）设PD=AD=1，求棱锥D-PBC的高．‎ ‎11.（11天津17）（本小题满分13分）如图，在四棱锥中，底面为 ‎ 平行四边形，，，为中点， 平面，，为中点．‎ ‎（Ⅰ）证明：//平面；‎ ‎（Ⅱ）证明：平面；‎ ‎13.如图，已知空间四边形中，，是的中点。‎ 求证：（1）平面CDE;‎ A E D B C （1） 平面平面。‎ ‎14、正方体中，求证：（1）；（2）.‎ A1‎ A B1‎ B C1‎ C D1‎ D G E F ‎15、正方体ABCD—A1B1C1D1中．(1)求证：平面A1BD∥平面B1D1C；‎ ‎ (2)若E、F分别是AA1，CC1的中点，求证：平面EB1D1∥平面FBD．‎ ‎18、（本小题满分13分）‎ 如图5所示，在四棱锥P－ABCD中，AB⊥平面PAD，AB∥CD，PD＝AD，E是PB的中点，F是DC上的点且DF＝AB，PH为△PAD边上的高。‎ ‎（1）证明：PH⊥平面ABCD；‎ ‎（2）若PH＝1，AD＝，FC＝1，求三棱锥E－BCF的体积；‎ ‎（3）证明：EF⊥平面PAB。‎