高考物理知识归纳：2力学模型及方法 5页

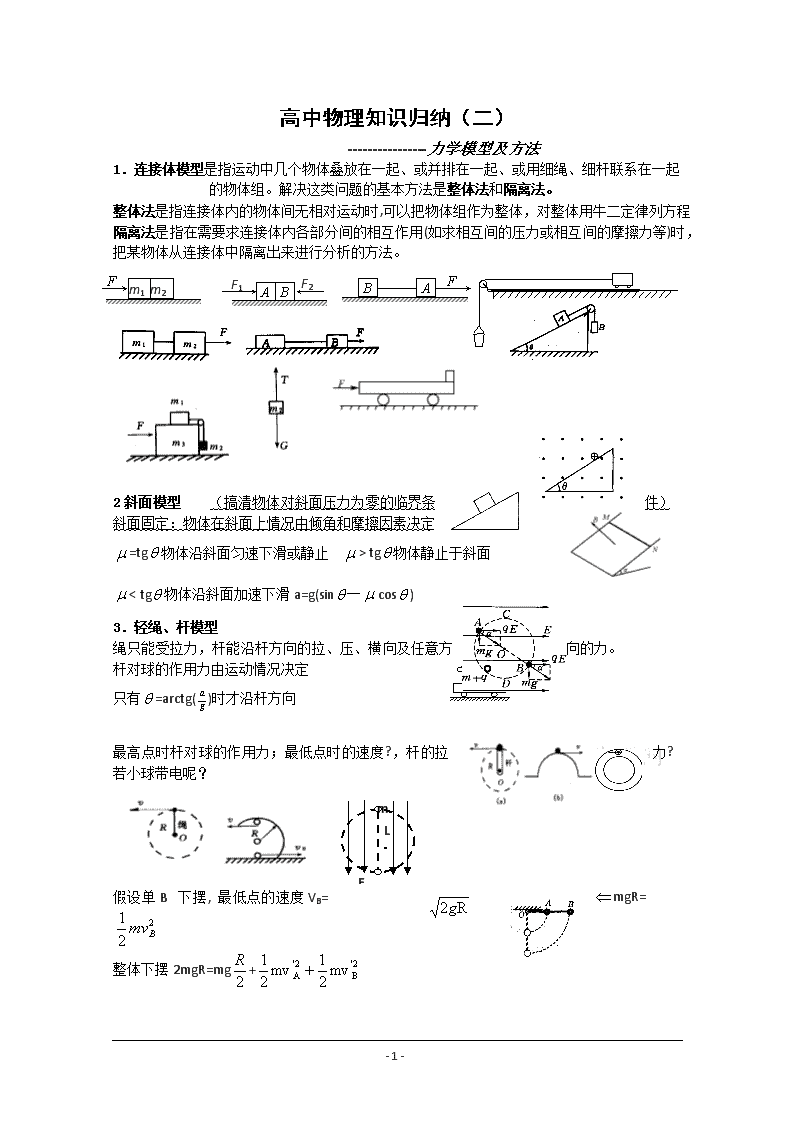
高中物理知识归纳（二）‎ ‎----------------力学模型及方法 ‎1．连接体模型是指运动中几个物体叠放在一起、或并排在一起、或用细绳、细杆联系在一起的物体组。解决这类问题的基本方法是整体法和隔离法。‎ 整体法是指连接体内的物体间无相对运动时,可以把物体组作为整体，对整体用牛二定律列方程 隔离法是指在需要求连接体内各部分间的相互作用(如求相互间的压力或相互间的摩擦力等)时，把某物体从连接体中隔离出来进行分析的方法。‎ B A F m2‎ m1‎ F B A F1‎ F2‎ ‎2斜面模型 （搞清物体对斜面压力为零的临界条件）‎ 斜面固定：物体在斜面上情况由倾角和摩擦因素决定 ‎=tg物体沿斜面匀速下滑或静止 > tg物体静止于斜面 ‎< tg物体沿斜面加速下滑a=g(sin一cos) ‎ ‎3．轻绳、杆模型 ‎╰‎ α 绳只能受拉力，杆能沿杆方向的拉、压、横向及任意方向的力。‎ 杆对球的作用力由运动情况决定 只有=arctg()时才沿杆方向 ‎ 最高点时杆对球的作用力；最低点时的速度?，杆的拉力?‎ 若小球带电呢？‎ E m，q L ‎·O 假设单B下摆,最低点的速度VB= mgR=‎ 整体下摆2mgR=mg+‎ - 5 -‎ ‎ = ； => VB=‎ 所以AB杆对B做正功，AB杆对A做负功 若 V0< ，运动情况为先平抛，绳拉直沿绳方向的速度消失 即是有能量损失，绳拉紧后沿圆周下落机械能守恒。而不能够整个过程用机械能守恒。‎ 求水平初速及最低点时绳的拉力？‎ 换为绳时:先自由落体,在绳瞬间拉紧(沿绳方向的速度消失)有能量损失(即v1突然消失),再v2下摆机械能守恒 例：摆球的质量为m，从偏离水平方向30°的位置由静释放，设绳子为理想轻绳，求：小球运动到最低点A时绳子受到的拉力是多少？‎ ‎4．超重失重模型 ‎ 系统的重心在竖直方向上有向上或向下的加速度(或此方向的分量ay)‎ 向上超重(加速向上或减速向下)F=m(g+a)；向下失重(加速向下或减速上升)F=m(g-a)‎ 难点：一个物体的运动导致系统重心的运动 ‎1到2到3过程中 (1、3除外)超重状态 ‎ 绳剪断后台称示数 系统重心向下加速F m a 图9‎ q 斜面对地面的压力? ‎ 地面对斜面摩擦力? ‎ 导致系统重心如何运动？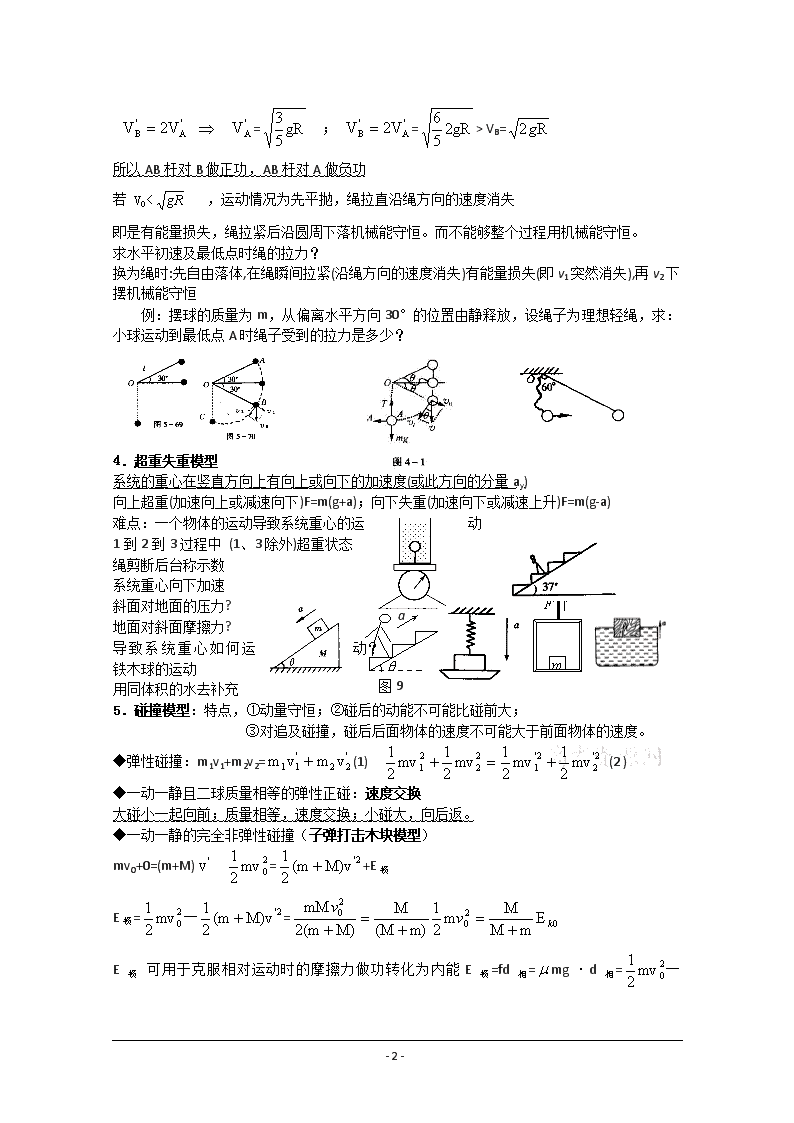‎ 铁木球的运动 用同体积的水去补充 ‎ ‎5．碰撞模型：特点，①动量守恒；②碰后的动能不可能比碰前大；‎ ③对追及碰撞，碰后后面物体的速度不可能大于前面物体的速度。‎ ‎◆弹性碰撞：m1v1+m2v2=(1) (2 ) ‎ ‎◆一动一静且二球质量相等的弹性正碰：速度交换 大碰小一起向前；质量相等，速度交换；小碰大，向后返。‎ ‎◆一动一静的完全非弹性碰撞（子弹打击木块模型）‎ mv0+0=(m+M) =+E损 ‎ E损=一=‎ E损 可用于克服相对运动时的摩擦力做功转化为内能E损=fd相=mg·d相=一 - 5 -‎ ‎1‎ ‎2‎ A v0‎ v s M v0‎ L v0‎ A B A B v0‎ ‎“碰撞过程”中四个有用推论 弹性碰撞除了遵从动量守恒定律外，还具备：碰前、碰后系统的总动能相等的特征，‎ 设两物体质量分别为m1、m2，碰撞前速度分别为υ1、υ2，碰撞后速度分别为u1、u2，即有 ： ‎ ‎ m1υ1+m2υ2=m1u1+m1u2‎ ‎ m1υ12+m2υ22=m1u12+m1u22‎ 碰后的速度u1和u2表示为： u1=υ1+υ2‎ u2=υ1+υ2‎ 推论一：如对弹性碰撞的速度表达式进行分析，还会发现：弹性碰撞前、后，碰撞双方的相对速度大小相等，即}： u2－u1=υ1－υ2‎ 推论二：如对弹性碰撞的速度表达式进一步探讨，当m1=m2时，代入上式得：。即当质量相等的两物体发生弹性正碰时，速度互换。‎ 推论三：完全非弹性碰撞碰撞双方碰后的速度相等的特征，即： u1=u2‎ 由此即可把完全非弹性碰撞后的速度u1和u2表为： u1=u2=‎ 例3：证明：完全非弹性碰撞过程中机械能损失最大。‎ 证明：碰撞过程中机械能损失表为： △E=m1υ12+m2υ22―m1u12―m2u22‎ 由动量守恒的表达式中得： u2=(m1υ1+m2υ2－m1u1)‎ 代入上式可将机械能的损失△E表为u1的函数为：‎ ‎△E=－u12－u1+[(m1υ12+m2υ22)－( m1υ1+m2υ2)2]‎ 这是一个二次项系数小于零的二次三项式，显然：当 u1=u2=时，‎ 即当碰撞是完全非弹性碰撞时，系统机械能的损失达到最大值 - 5 -‎ ‎△Em=m1υ12+m2υ22 －‎ 推论四：碰撞过程中除受到动量守恒以及能量不会增加等因素的制约外，还受到运动的合理性要求的制约，比如，某物体向右运动，被后面物体追及而发生碰撞，被碰物体运动速度只会增大而不应该减小并且肯定大于或者等于（不小于）碰撞物体的碰后速度。‎ ‎6．人船模型：一个原来处于静止状态的系统，在系统内发生相对运动的过程中，‎ 在此方向遵从动量守恒：mv=MV ms=MS s+S=d s= M/m=Lm/LM 载人气球原静止于高h的高空，气球质量为M，人的质量为m．若人沿绳梯滑至地面，则绳梯至少为多长？‎ ‎ ‎ ‎20m S1‎ S2‎ M m O R ‎7．弹簧振子模型：F=-Kx （X、F、a、v、A、T、f、EK、EP等量的变化规律）水平型 竖直型 ‎8．单摆模型：T=2 （类单摆） 利用单摆测重力加速度 ‎9．波动模型：特点:传播的是振动形式和能量,介质中各质点只在平衡位置附近振动并不随波迁移。‎ ①各质点都作受迫振动， ②起振方向与振源的起振方向相同， ③离源近的点先振动，‎ ④没波传播方向上两点的起振时间差=波在这段距离内传播的时间⑤波源振几个周期波就向外传几个波长。波从一种介质传播到另一种介质,频率不改变, 波速v=s/t=/T=f ‎ 波速与振动速度的区别 波动与振动的区别：波的传播方向质点的振动方向（同侧法）‎ 知波速和波形画经过Δt后的波形（特殊点画法和去整留零法）‎ 物理解题方法：如整体法、假设法、极限法、逆向思维法、物理模型法、等效法、物理图像法等．‎ 模型法常常有下面三种情况 ‎（1）物理对象模型：用来代替由具体物质组成的、代表研究对象的实体系统，称为对象模型（也可称为概念模型），即把研究的对象的本身理想化．常见的如“力学”中有质点、刚体、杠杆、轻质弹簧、单摆、弹簧振子、弹性体、绝热物质等；‎ ‎（2）条件模型：把研究对象所处的外部条件理想化，排除外部条件中干扰研究对象运动变化的次要因素，突出外部条件的本质特征或最主要的方面，从而建立的物理模型称为条件模型．‎ ‎（3）过程模型：把具体过理过程纯粹化、理想化后抽象出来的一种物理过程，称过程模型 其它的碰撞模型：‎ - 5 -‎ v0‎ A B C ‎1‎ ‎2‎ A A B C - 5 -‎