北京丰台区高考二模数学文科试题word含解析 15页

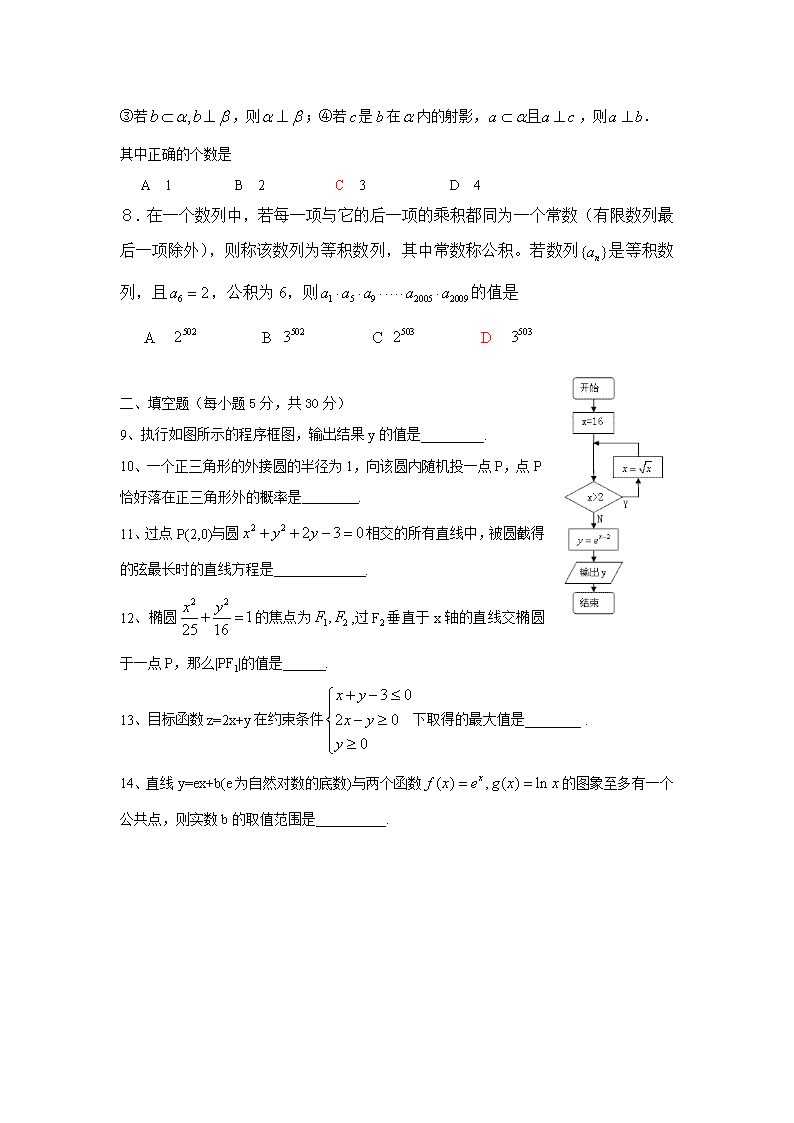
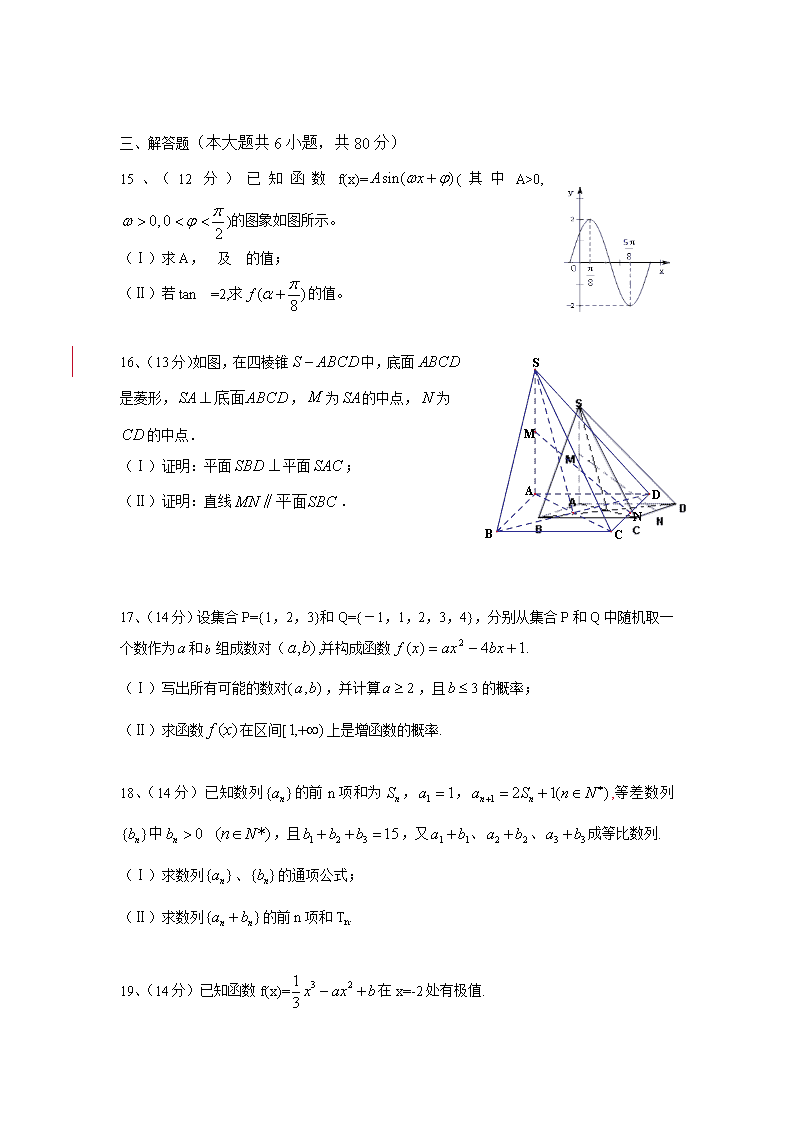
丰台区2010年高三统一练习（二）‎ 数学（文科）‎ 一、选择题（每小题5分，共40分）‎ ‎1、已知向量（1，），（，1），若与的夹角为，则实数的值为 A． B． C． D．‎ ‎2、设集合A=，B=，则等于 A B C D ‎ ‎3、设p、q是简单命题，则为真是为真的 A 充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 ‎4、在中，sin(A+B)=sin(A-B),则一定是 A 等腰三角形 B等边三角形 C 直角三角形 D 锐角三角形 ‎5、甲、乙两名运动员的5次测试成绩如下图所示 甲 茎 乙 ‎ 7 7‎ ‎8‎ ‎6 8‎ ‎8 6 2‎ ‎9‎ ‎3 6 7‎ 设分别表示甲、乙两名运动员测试成绩的标准差，分别表示甲、乙两名运动员测试成绩的平均数，则有 A ， B ， ‎ C ， D ， ‎ ‎6、已知函数f(x)是偶函数，在（0，+¥）上导数>0恒成立，则下列不等式成立的是 Ａ　f(-3)0,)的图象如图所示。‎ ‎（Ⅰ）求A，w及j的值； ‎ ‎（Ⅱ）若tana=2,求的值。‎ ‎16、（13分）如图，在四棱锥中，底面是菱形，，为的中点，为的中点．‎ ‎（Ⅰ）证明：平面平面； ‎ ‎（Ⅱ）证明：直线．‎ ‎17、（14分）设集合P={1，2，3}和Q={－1，1，2，3，4}，分别从集合P和Q中随机取一个数作为和组成数对（,并构成函数 ‎（Ⅰ）写出所有可能的数对(，并计算，且的概率；‎ ‎（Ⅱ）求函数在区间[上是增函数的概率.‎ ‎18、（14分）已知数列的前n项和为，，,等差数列中 ，且，又、、成等比数列.‎ ‎（Ⅰ）求数列、的通项公式；‎ ‎（Ⅱ）求数列的前n项和Tn.‎ ‎19、（14分）已知函数f(x)=在x=-2处有极值.‎ ‎（Ⅰ）求函数f(x)的单调区间；‎ ‎（Ⅱ）若函数f(x)在区间[-3,3]上有且仅有一个零点，求b的取值范围.‎ ‎20、（13分）已知椭圆经过点，过右焦点F且不与x轴重合的动直线L交椭圆于两点，当动直线L的斜率为2时，坐标原点O到L的距离为． ‎ ‎(Ⅰ) 求椭圆的方程；‎ ‎(Ⅱ) 过F的另一直线交椭圆于两点，且，当四边形的面积S=时，求直线L的方程．‎ 丰台区2010年高三统一练习（二）‎ 数学（文科）‎ 一、选择题（每小题5分，共40分）‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ 答案 C D A C B B C D 二、填空题（每小题5分，共30分）‎ ‎9、1 ； 10、 ； 11、x-2y-2=0 ； 12、 ； 13、6 ； 14、 [-2,0]。‎ 三、解答题（本大题共6小题，共80分）‎ ‎15、（12分）已知函数f(x)=(其中A>0,)的图象如图所示。‎ ‎（Ⅰ）求A，w及j的值； ‎ ‎（Ⅱ）若tana=2,求的值。‎ 解：（Ⅰ）由图知A=2, ……………………1分 T=2()=p,‎ ‎∴w=2, ……………………3分 ‎∴f(x)=2sin(2x+j)‎ 又∵=2sin(+j)=2, ‎ ‎∴sin(+j)=1, ‎ ‎∴+j=,j=+,(kÎZ)‎ ‎∵,∴j= ……………………6分 由（Ⅰ）知：f(x)=2sin(2x+)，‎ ‎∴=2sin(2a+)=2cos2a=4cos2a-2…………9分 ‎∵tana=2, ∴sina=2cosa,‎ 又∵sin2a+cos2a=1, ∴cos2a=,‎ ‎∴= ……………………12分 ‎ ‎16、（13分）如图，在四棱锥中，底面是菱形，，为的中点，为的中点．‎ ‎（Ⅰ）证明：平面平面； ‎ ‎（Ⅱ）证明：直线．‎ 证明：（Ⅰ）∵ABCD是菱形，‎ ‎ ∴BD^AC， ………………………………1分 ‎∵，∴BD^SA， ……………2分 ‎∵SA与AC交于A,‎ ‎∴BD^平面SAC, …………………………………4分 ‎∵平面 ‎∴平面平面 …………………6分 ‎（Ⅱ）取SB中点E，连接ME，CE，‎ ‎∵M为SA中点，∴MEAB且ME=AB, ………8分 又∵是菱形，N为的中点，‎ ‎∴CNAB且CN=CD=AB, …………………10分 ‎∴CNEM,且CN=EM，‎ ‎∴四边形CNME是平行四边形，‎ ‎∴MNCE, …………………12分 又MNË平面SBC, CEÌ平面SBC, ‎ ‎∴直线 …………………13分 ‎17、（14分）设集合P={1，2，3}和Q={－1，1，2，3，4}，分别从集合P和Q中随机取一个数作为和组成数对（，并构成函数．‎ ‎（Ⅰ）写出所有可能的数对（，并计算，且的概率；‎ ‎（Ⅱ）求函数在区间[上是增函数的概率．‎ 解: （Ⅰ）所有基本事件如下:‎ ‎(1,-1),(1,1),(1,2),(1,3),(1,4), ‎ ‎(2,-1),(2,1),(2,2),(2,3),(2,4),‎ ‎(3,-1),(3,1),(3,2),(3,3),(3,4) ，共有15个。………………………………4分 设事件“，且”为A,‎ 则事件A包含的基本事件有8个, ………………………………… 6分 所以P(A)=。 ……………………………………………8分 ‎（Ⅱ）设事件“在区间上为增函数”为B,‎ 因函数的图象的对称轴为 且>0，‎ 所以要使事件B发生，只需。…………………………10分 由满足题意的数对有（1，-1）、（2，-1）、（2，1）、（3，-1）、（3，1），共5个，‎ ‎ …………………………12分 所以，P(B)= . …………………………14分 ‎18、（14分）已知数列的前n项和为，，,等差数列中，，且，又、、成等比数列.‎ ‎（Ⅰ）求数列、的通项公式；‎ ‎（Ⅱ）求数列的前n项和Tn.‎ 解：（Ⅰ）∵，，‎ ‎∴，‎ ‎ ∴， ‎ ‎∴， ‎ ‎∴ …………………………3分 ‎ 而，∴‎ ‎∴数列是以1为首项，3为公比的等比数列，‎ ‎∴ …………………………5分 ‎∴， ‎ 在等差数列中，∵，∴。‎ 又因、、成等比数列，设等差数列的公差为d，‎ ‎∴（） ………………………………7分 解得d=-10,或d=2, ∵，∴舍去d=-10，取d=2， ∴b1=3, ‎ ‎∴bn=2n+1， ………………………………9分 ‎（Ⅱ）由（Ⅰ）知 ‎∴‎ ‎=(‎ ‎=‎ ‎= ………………………………14分 ‎19、（14分）已知函数f(x)=在x=-2处有极值. ‎ ‎（Ⅰ）求函数f(x)的单调区间；‎ ‎（Ⅱ）若函数f(x)在区间[-3,3]上有且仅有一个零点，求b的取值范围。‎ 解: （Ⅰ） …………………………………………1分 由题意知: ,得a=-1，………………………2分 ‎∴，‎ 令，得x<-2或x>0, ………………………4分 ‎ 令，得-2f(x)，则实数x的取值范围是 ‎(A) ‎ ‎(B) ‎ ‎(C) ‎ ‎(D) ‎ x y O A C ‎(1,1)‎ B ‎7．从如图所示的正方形OABC区域内任取一个点，则点M取自阴影部分的概率为 ‎(A) ‎ ‎(B) ‎ ‎(C) ‎ ‎(D) ‎ ‎8．对于定义域和值域均为[0，1]的函数f(x)，定义，，…，，n=1，2，3，…．满足的点x∈[0，1]称为f的阶周期点．设 则f的阶周期点的个数是 ‎(A) 2n ‎(B) 2(2n-1)‎ ‎(C) 2n ‎(D) 2n2 ‎ A A x y O 二、填空题：本大题共6小题，每小题5分，共30分．‎ ‎9．如图所示，在平面直角坐标系xOy中，角α的终边与单位圆交于点A，‎ 点A的纵坐标为，则cosα= ． ‎ ‎10．双曲线的焦点在x轴上，实轴长为4，离心率为3，则该双曲线的标准方 程为 ，渐近线方程为 ．‎ C D MB N O B A P ‎11．已知圆M：x2+y2-2x-4y+1=0，则圆心M到直线（t为参数）的距离为 ．‎ ‎12．如图所示，过⊙O外一点A作一条直线与⊙O交于C，D两点，AB切⊙O 于B，弦MN过CD的中点P．已知AC=4，AB=6，则MP·NP= ．‎ ‎13．对某种花卉的开放花期追踪调查，调查情况如下：‎ 花期（天）[来源:Z+xx+k.Com]‎ ‎11～13‎ ‎14～16‎ ‎17～19‎ ‎20～22‎ 个数 ‎20‎ ‎40‎ ‎30‎ ‎10‎ 则这种卉的平均花期为___天． ‎ ‎14．将全体正奇数排成一个三角形数阵：‎ ‎ 1‎ ‎ 3 5‎ ‎ 7 9 11‎ ‎ 13 15 17 19‎ ‎ ……‎ ‎ 按照以上排列的规律，第n 行（n ≥3）从左向右的第3个数为 ．‎ 三、解答题：本大题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程．‎ ‎15.（本小题共13分）‎ 在△ABC中，a，b，c分别为内角A，B，C的对边，且b2+c2-a2=bc．‎ ‎（Ⅰ）求角A的大小；‎ ‎（Ⅱ）设函数，当取最大值时，判断△ABC的形状．‎ ‎16.（本小题共14分）‎ P A B C D Q M 如图，在四棱锥P-ABCD中，底面ABCD为直角梯形，AD//BC，∠ADC=90°，平面PAD⊥底面ABCD，Q为AD的中点，M是棱PC上的点，PA=PD=2，BC=AD=1，CD=．‎ ‎（Ⅰ）若点M是棱PC的中点，求证：PA // 平面BMQ；‎ ‎（Ⅱ）求证：平面PQB⊥平面PAD； ‎ ‎（Ⅲ）若二面角M-BQ-C为30°，设PM=tMC，试确定t的值 ．‎ ‎17.（本小题共13分）‎ 某商场在店庆日进行抽奖促销活动，当日在该店消费的顾客可参加抽奖．抽奖箱中有大小完全相同的4个小球，分别标有字“生”“意”“兴”“隆”．顾客从中任意取出1个球，记下上面的字后放回箱中，再从中任取1个球，重复以上操作，最多取4次，并规定若取出“隆”字球，则停止取球．获奖规则如下：依次取到标有“生”“意”“兴”“隆”字的球为一等奖；不分顺序取到标有“生”“意”“兴”“隆”字的球，为二等奖；取到的4个球中有标有“生”“意”“兴”三个字的球为三等奖．‎ ‎（Ⅰ）求分别获得一、二、三等奖的概率；‎ ‎（Ⅱ）设摸球次数为，求的分布列和数学期望．‎ ‎18.（本小题共13分）‎ 已知函数，为函数的导函数． ‎ ‎（Ⅰ）设函数f(x)的图象与x轴交点为A，曲线y=f(x)在A点处的切线方程是，求的值；‎ ‎（Ⅱ）若函数，求函数的单调区间．‎ ‎ ‎ ‎19.（本小题共14分） ‎ 已知点，，动点P满足，记动点P的轨迹为W．‎ ‎（Ⅰ）求W的方程；‎ ‎（Ⅱ）直线与曲线W交于不同的两点C，D，若存在点，使得成立，求实数m的取值范围．‎ ‎20.（本小题共13分）‎ 已知，或1，，对于，表示U和V中相对应的元素不同的个数．‎ ‎（Ⅰ）令，存在m个，使得，写出m的值；‎ ‎（Ⅱ）令，若，求证：；‎ ‎（Ⅲ）令，若，求所有之和．‎