全国高考新课标卷理科数学试题解析 6页

‎2018年普通高等学校招生全国统一考试新课标1卷 理科数学 注意事项：‎ ‎1．答卷前，考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上。‎ ‎2．回答选择题时，选出每小题答案后，用铅笔把答题卡对应题目的答案标号涂黑。如需改动，用橡皮擦干净后，再选涂其它答案标号。回答非选择题时，将答案写在答题卡上。写在本试卷上无效。‎ ‎3．考试结束后，将本试卷和答题卡一并交回。‎ 一、选择题：本题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。‎ ‎1．设z=+2i，则|z|=‎ A．0 B． C．1 D． 解析：选C z=+2i=-i+2i=i ‎2．已知集合A={x|x2-x-2>0}，则∁RA =‎ A．{x|-12} D．{x|x≤-1}∪{x|x≥2} ‎ 解析：选B A={x|x<-1或x>2} ‎ ‎3．某地区经过一年的新农村建设，农村的经济收入增加了一倍，实现翻番，为更好地了解该地区农村的经济收入变化情况，统计了该地区新农村建设前后农村的经济收入构成比例，得到如下饼图：‎ ‎ ‎ 建设前经济收入构成比例 建设后经济收入构成比例 则下面结论中不正确的是 A．新农村建设后，种植收入减少 B．新农村建设后，其他收入增加了一倍以上 C．新农村建设后，养殖收入增加了一倍 D．新农村建设后，养殖收入与第三产业收入的总和超过了经济收入的一半 解析：选A ‎4．设Sn为等差数列{an}的前n项和，若3S3=S2+S4，a1=2，则a5=‎ A．-12 B．-10 C．10 D．12‎ 解析：选 ∵3(3a1+3d)=(2a1+d )+(4a1+6d) a1=2 ∴d=-3 a5=-10‎ ‎5．设函数f(x)=x3+(a-1)x2+ax，若f(x)为奇函数，则曲线y=f(x)在点(0,0)处的切线方程为 A．y=-2x B．y=-x C．y=2x D．y=x 解析：选D ∵f(x)为奇函数 ∴a=1 ∴f(x)=x3+x f′(x)=3x2+1 f′(0)=1 故选D ‎6．在ΔABC中，AD为BC边上的中线，E为AD的中点，则=‎ A． - B． - C． + D． + 解析：选A 结合图形，=- (+)=- -=- -(-)= - ‎7．某圆柱的高为2，底面周长为16，其三视图如图．圆柱表面上的点M在正视图上的对应点为A，圆柱表面上的点N在左视图上的对应点为B，则在此圆柱侧面上，从M到N的路径中，最短路径的长度为 A．2 B．2 C．3 D．2‎ 解析：选B 所求最短路径即四份之一圆柱侧面展开图对角线的长 ‎8．设抛物线C：y2=4x的焦点为F，过点（–2，0）且斜率为的直线与C交于M，N两点，则·=‎ A．5 B．6 C．7 D．8‎ 解析：选D F(1,0)，MN方程为y= (x+2),代入抛物线方程解得交点M(1,2),N(4,4),则=(0,2),=(3,4)‎ ‎∴·=8‎ ‎9．已知函数f(x)= ，g(x)=f(x)+x+a．若g（x）存在2个零点，则a的取值范围是 A．[–1，0） B．[0，+∞） C．[–1，+∞） D．[1，+∞）‎ 解析：选C g(x)=0即f(x)=-x-a，即y=f(x)图象与直线y=-x-a有2个交点，结合y=f(x)图象可知-a<1‎ ‎10．下图来自古希腊数学家希波克拉底所研究的几何图形．此图由三个半圆构成，三个半圆的直径分别为直角三角形ABC的斜边BC，直角边AB，AC．△ABC的三边所围成的区域记为I，黑色部分记为II，其余部分记为III．在整个图形中随机取一点，此点取自I，II，III的概率分别记为p1，p2，p3，则 A．p1=p2 B．p1=p3‎ C．p2=p3 D．p1=p2+p3‎ 解析：选A ∵AC=3，AB=4，∴BC=5，∴AC=，AB=2 , BC= ‎∴以AC和AB为直径的两个半圆面积之和为×π×()2+×π×22=π ‎∴以BC为直径的半圆面积与三角形ABC的面积之差为×π×()2- ×3×4=π-6；‎ ‎∴两个月牙形（图中阴影部分）的面积之和等于π-(π-6)=6=ΔABC面积 ‎∴p1=p2‎ ‎11．已知双曲线C： - y2 =1，O为坐标原点，F为C的右焦点，过F的直线与C的两条渐近线的交点分别为M、N.若ΔOMN为直角三角形，则|MN|=‎ A． B．3 C．2 D．4‎ 解析：选B 依题F(2,0),曲线C的渐近线为y=±x,MN的斜率为，方程为y=(x-2),联立方程组解得M(,- ),N(3, ),∴|MN|=3‎ ‎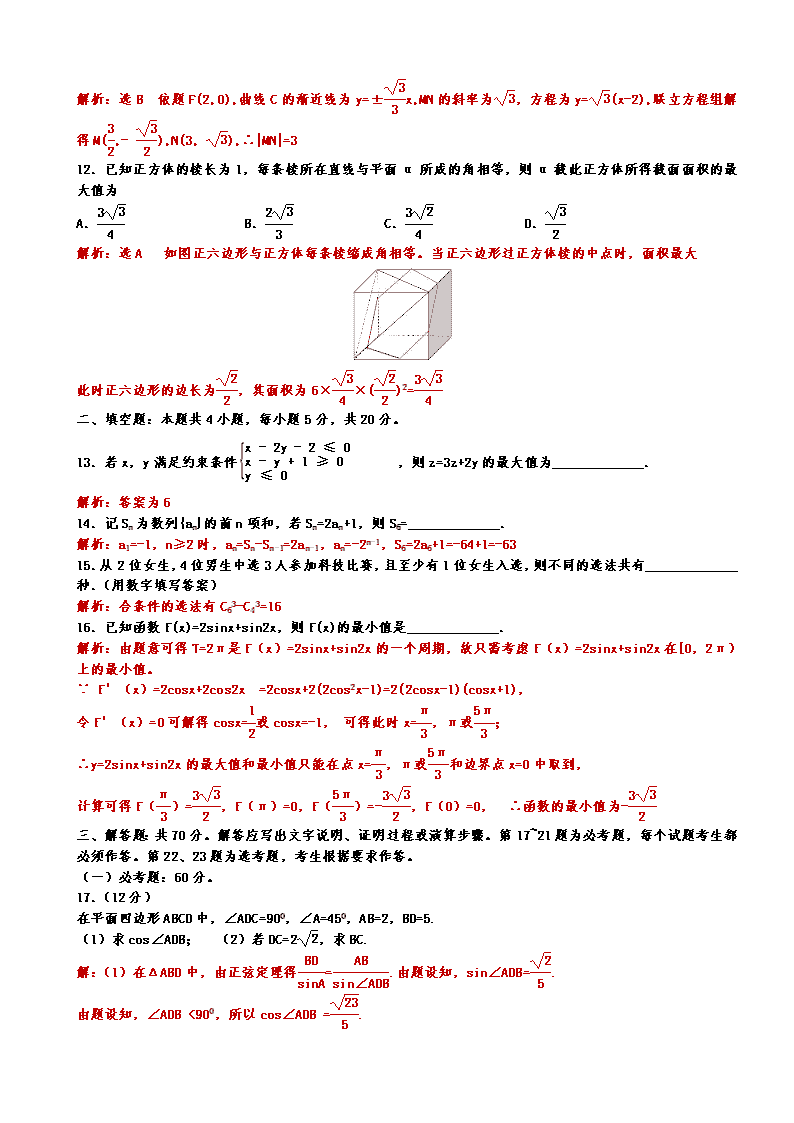12．已知正方体的棱长为1，每条棱所在直线与平面α所成的角相等，则α截此正方体所得截面面积的最大值为 A． B． C． D． 解析：选A 如图正六边形与正方体每条棱缩成角相等。当正六边形过正方体棱的中点时，面积最大 此时正六边形的边长为，其面积为6××()2= 二、填空题：本题共4小题，每小题5分，共20分。‎ ‎13．若x，y满足约束条件，则z=3z+2y的最大值为_____________．‎ 解析：答案为6‎ ‎14．记Sn为数列{an}的前n项和，若Sn=2an+1，则S6=_____________．‎ 解析：a1=-1，n≥2时，an=Sn-Sn-1=2an-1，an=-2n-1，S6=2a6+1=-64+1=-63‎ ‎15．从2位女生，4位男生中选3人参加科技比赛，且至少有1位女生入选，则不同的选法共有_____________种．（用数字填写答案）‎ 解析：合条件的选法有C63-C43=16‎ ‎16．已知函数f(x)=2sinx+sin2x，则f(x)的最小值是_____________．‎ 解析：由题意可得T=2π是f（x）=2sinx+sin2x的一个周期，故只需考虑f（x）=2sinx+sin2x在[0，2π）上的最小值。‎ ‎∵ f′（x）=2cosx+2cos2x =2cosx+2(2cos2x-1)=2(2cosx-1)(cosx+1)，‎ 令f′（x）=0可解得cosx=或cosx=-1， 可得此时x=，π或；‎ ‎∴y=2sinx+sin2x的最大值和最小值只能在点x=，π或和边界点x=0中取到，‎ 计算可得f（）=，f（π）=0，f（）=-，f（0）=0， ∴函数的最小值为- 三、解答题：共70分。解答应写出文字说明、证明过程或演算步骤。第17~21题为必考题，每个试题考生都必须作答。第22、23题为选考题，考生根据要求作答。‎ ‎（一）必考题：60分。‎ ‎17．（12分）‎ 在平面四边形ABCD中，∠ADC=900，∠A=450，AB=2，BD=5.‎ ‎（1）求cos∠ADB； （2）若DC=2，求BC.‎ 解：（1）在ΔABD中，由正弦定理得=.由题设知，sin∠ADB=.‎ 由题设知，∠ADB <900，所以cos∠ADB =.‎ ‎（2）由题设及（1）知，cos∠BDC= sin∠ADB=.‎ 在ΔBCD中，由余弦定理得BC2=BD2+DC2-2BD·DC·cos∠BDC=25 所以BC=5.‎ ‎18．（12分）‎ 如图，四边形ABCD为正方形，E，F分别为AD，BC的中点，以DF为折痕把ΔDFC折起，使点C到达点P的位置，且PF⊥BF.‎ ‎（1）证明：平面PEF⊥平面ABFD；‎ ‎（2）求DP与平面ABFD所成角的正弦值.‎ 解：（1）由已知可得，BF⊥PF，BF⊥EF，所以BF⊥平面PEF.‎ 又BF平面ABFD，所以平面PEF⊥平面ABFD.‎ ‎（2）作PH⊥EF，垂足为H.由（1）得，PH⊥平面ABFD.‎ 以H为坐标原点，的方向为y轴正方向，||为单位长，建立如图所示的空间直角坐标系H−xyz.‎ 由（1）可得，DE⊥PE.又DP=2，DE=1，所以PE=.又PF=1，EF=2，故PE⊥PF. 可得PH=,EH=.‎ 则H(0,0,0),P(0,0, ),D(-1,- ,0 ), =(1, ,),‎ =(0,0, )为平面ABFD的法向量.‎ 设DP与平面ABFD所成角为θ，则sinθ=||=.‎ 所以DP与平面ABFD所成角的正弦值为.‎ ‎19．（12分）‎ 设椭圆C: + y2 =1的右焦点为F，过F的直线l与C交于A,B两点，点M的坐标为(2,0).‎ ‎（1）当l与x轴垂直时，求直线AM的方程；‎ ‎（2）设O为坐标原点，证明：∠OMA=∠OMB.‎ 解：（1）由已知得F(1,0)，l的方程为x=1.‎ 由已知可得，点A的坐标为(1, )或(1,- ).‎ 所以AM的方程为y= - x+或y= x-.‎ ‎（2）当l与x轴重合时，∠OMA=∠OMB =00.‎ 当l与x轴垂直时，OM为AB的垂直平分线，所以∠OMA=∠OMB.‎ 当l与x轴不重合也不垂直时，设l的方程为y=k(x-1)(k≠0)，A(x1,y1)，B(x2,y2)，‎ 则x1<,x2<，直线MA，MB的斜率之和为kMA+kMB=+.‎ 由y1=kx1-k, y2=kx2-k得kMA+kMB= 将y=k(x-1)代入 + y2 =1得(2k2+1)x2-4k2x+2k2-2=0 所以，x1+x2=, x1x2=.‎ 则2kx1x2-3k(x1+x2)+4k ==0‎ 从而kMA+kMB=0，故MA，MB的倾斜角互补，所以∠OMA=∠OMB.‎ 综上，∠OMA=∠OMB.‎ ‎20．（12分）‎ 某工厂的某种产品成箱包装，每箱200件，每一箱产品在交付用户之前要对产品作检验，如检验出不合格品，则更换为合格品．检验时，先从这箱产品中任取20件作检验，再根据检验结果决定是否对余下的所有产品作检验，设每件产品为不合格品的概率都为p(00；当p∈(0.1,1)时，f′(p)<0.‎ 所以f(p)的最大值点为p0=0.1.‎ ‎（2）由（1）知，p=0.1.‎ ‎（i）令Y表示余下的180件产品中的不合格品件数，依题意知Y～B(180,0.1)，X=40+25Y，‎ 所以EX=E(40+25Y)=40+25EY=40+25×180×0.1=490.‎ ‎（ii）如果对余下的产品作检验，则这一箱产品所需要的检验费为400元.‎ 由于EX>400，故应该对余下的产品作检验.‎ ‎21．（12分）‎ 已知函数f(x)= - x+alnx．‎ ‎（1）讨论f(x)的单调性；‎ ‎（2）若f(x)存在两个极值点x1,x2，证明：2，令f′(x)=0得，x=或x=.‎ 当x∈(0, )∪(,+∞)时，f′(x)<0；‎ 当x∈(,)时，f′(x)>0.‎ 所以f(x)在(0, )、(,+∞)单调递减，在(,)单调递增.‎ ‎（2）由（1）知，f(x)存在两个极值点当且仅当a>2.‎ 由于f(x)的两个极值点x1,x2满足x2-ax+1=0，所以x1x2=1，不妨设x11.‎ 由于= - -1+a= -2+ a=-2+ a，‎ 所以1的解集；‎ ‎（2）若x∈(0,1)时不等式f(x)>x成立，求a的取值范围.‎ 解:（1）当a=1时，f(x)=|x+1|-|x-1|，即f(x)= 故不等式f(x)>1的解集为(,+∞)．‎ ‎（2）当x∈(0,1)时|x+1|-|ax-1|>x成立等价于当x∈(0,1)时|ax-1|<1成立．‎ 若a≤0，则当x∈(0,1)时|ax-1|≥1；‎ 若a>0，|ax-1|<1的解集为(0, )，所以≥1，故(0,2]．‎ 综上，a的取值范围为(0,2]．‎