全国卷高考复习平面向量知识总结题型 7页

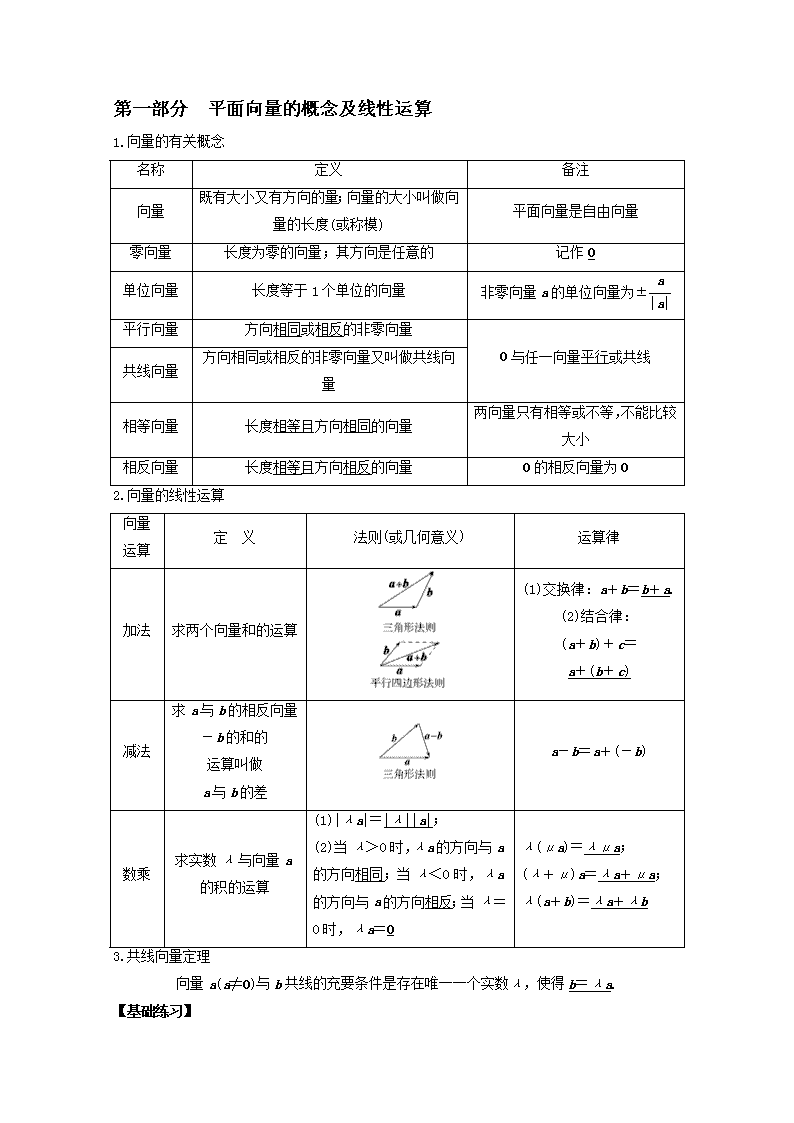
第一部分　平面向量的概念及线性运算 ‎1.向量的有关概念 名称 定义 备注 向量 既有大小又有方向的量；向量的大小叫做向量的长度(或称模)‎ 平面向量是自由向量 零向量 长度为零的向量；其方向是任意的 记作0‎ 单位向量 长度等于1个单位的向量 非零向量a的单位向量为± 平行向量 方向相同或相反的非零向量 ‎0与任一向量平行或共线 共线向量 方向相同或相反的非零向量又叫做共线向量 相等向量 长度相等且方向相同的向量 两向量只有相等或不等，不能比较大小 相反向量 长度相等且方向相反的向量 ‎0的相反向量为0‎ ‎2.向量的线性运算 向量运算 定　义 法则(或几何意义)‎ 运算律 加法 求两个向量和的运算 ‎(1)交换律：a＋b＝b＋a. ‎ ‎(2)结合律：‎ ‎(a＋b)＋c＝‎ a＋(b＋c)‎ 减法 求a与b的相反向量 ‎－b的和的 运算叫做 a与b的差 a－b＝a＋(－b)‎ 数乘 求实数λ与向量a的积的运算 ‎(1)|λa|＝|λ||a|；‎ ‎(2)当λ＞0时，λa的方向与a的方向相同；当λ＜0时，λa的方向与a的方向相反；当λ＝0时，λa＝0‎ λ(μa)＝λμa；‎ ‎(λ＋μ)a＝λa＋μa；‎ λ(a＋b)＝λa＋λb ‎3.共线向量定理 向量a(a≠0)与b共线的充要条件是存在唯一一个实数λ，使得b＝λa.‎ ‎【基础练习】‎ ‎1.判断正误(在括号内打“√”或“×”)‎ ‎(1)零向量与任意向量平行.(　　)‎ ‎(2)若a∥b，b∥c，则a∥c.(　　)‎ ‎(3)向量与向量是共线向量，则A，B，C，D四点在一条直线上.(　　)‎ ‎(4)当两个非零向量a，b共线时，一定有b＝λa，反之成立.(　　)‎ ‎(5)在△ABC中，D是BC中点，则＝(＋).(　　)‎ ‎2.给出下列命题：①零向量的长度为零，方向是任意的；②若a，b都是单位向量，则a＝b；③向量与相等.则所有正确命题的序号是(　　)‎ A.① B.③ C.①③ D.①②‎ ‎3.(2017·枣庄模拟)设D为△ABC所在平面内一点，＝－＋，若＝λ(λ∈R)，则λ＝(　　)‎ A.2 B.3 C.－2 D.－3‎ ‎4.(2015·全国Ⅱ卷)设向量a，b不平行，向量λa＋b与a＋2b平行，则实数λ＝____________.‎ ‎5.(必修4P92A12改编)已知▱ABCD的对角线AC和BD相交于O，且＝a，＝b，则＝______，＝________(用a，b表示).‎ ‎6.(2017·嘉兴七校联考)设D，E分别是△ABC的边AB，BC上的点，AD＝AB，BE＝BC，若＝λ1＋λ2(λ1，λ2为实数)，则λ1＝________，λ2＝________.‎ 考点一　平面向量的概念 ‎【例1】 下列命题中，不正确的是________(填序号).‎ ‎①若|a|＝|b|，则a＝b；‎ ‎②若A，B，C，D是不共线的四点，则“＝”是“四边形ABCD为平行四边形”的充要条件；‎ ‎③若a＝b，b＝c，则a＝c.‎ ‎【训练1】 下列命题中，正确的是________(填序号).‎ ‎①有向线段就是向量，向量就是有向线段；‎ ‎②向量a与向量b平行，则a与b的方向相同或相反；‎ ‎③两个向量不能比较大小，但它们的模能比较大小.‎ 解析　①不正确，向量可以用有向线段表示，但向量不是有向线段，有向线段也不是向量；‎ ‎②不正确，若a与b中有一个为零向量，零向量的方向是不确定的，故两向量方向不一定相同或相反；‎ ‎③正确，向量既有大小，又有方向，不能比较大小；向量的模均为实数，可以比较大小.‎ 答案　③‎ 考点二　平面向量的线性运算 ‎【例2】 (2017·潍坊模拟)在△ABC中，P，Q分别是AB，BC的三等分点，且AP＝AB，BQ＝BC.若＝a，＝b，则＝(　　)‎ A.a＋b B.－a＋b C.a－b D.－a－b ‎【训练2】 (1)如图，正方形ABCD中，点E是DC的中点，点F是BC的一个靠近B点的三等分点，那么等于(　　)‎ A.－ B.＋ C.＋ D.－ 考点三　共线向量定理及其应用 ‎【例3】 设两个非零向量a与b不共线.‎ ‎(1)若＝a＋b，＝2a＋8b，＝3(a－b).求证：A，B，D三点共线；‎ ‎(2)试确定实数k，使ka＋b和a＋kb共线.‎ ‎【训练3】已知向量＝a＋3b，＝5a＋3b，＝－3a＋3b，则(　　)‎ A.A，B，C三点共线 B.A，B，D三点共线 C.A，C，D三点共线 D.B，C，D三点共线 第二部分　平面向量基本定理与坐标表示 ‎1.平面向量的基本定理 如果e1，e2是同一平面内的两个不共线向量，那么对于这一平面内的任意向量a，有且只有一对实数λ1，λ2，使a＝λ1e1＋λ2e2.‎ 其中，不共线的向量e1，e2叫做表示这一平面内所有向量的一组基底.‎ ‎2.平面向量的正交分解 把一个向量分解为两个互相垂直的向量，叫做把向量正交分解.‎ ‎3.平面向量的坐标运算 ‎(1)向量加法、减法、数乘向量及向量的模 设a＝(x1，y1)，b＝(x2，y2)，则 a＋b＝(x1＋x2，y1＋y2)，a－b＝(x1－x2，y1－y2)，λa＝(λx1，λy1)，|a|＝.‎ ‎(2)向量坐标的求法 ‎①若向量的起点是坐标原点，则终点坐标即为向量的坐标.‎ ‎②设A(x1，y1)，B(x2，y2)，则＝(x2－x1，y2－y1)，||＝.‎ ‎4.平面向量共线的坐标表示 设a＝(x1，y1)，b＝(x2，y2)，则a∥b⇔x1y2－x2y1＝0.‎ ‎【基础练习】‎ ‎1.(2017·东阳月考)已知向量a＝(2，4)，b＝(－1，1)，则2a＋b等于(　　)‎ A.(5，7) B.(5，9) C.(3，7) D.(3，9)‎ ‎2.(2015·全国Ⅰ卷)已知点A(0，1)，B(3，2)，向量＝(－4，－3)，则向量＝(　　)‎ A.(－7，－4) B.(7，4)‎ C.(－1，4) D.(1，4)‎ ‎3.(2016·全国Ⅱ卷)已知向量a＝(m，4)，b＝(3，－2)，且a∥b，则m＝________.‎ ‎4.(必修4P101A3改编)已知▱ABCD的顶点A(－1，－2)，B(3，－1)，C(5，6)，则顶点D的坐标为________.‎ 考点一　平面向量基本定理及其应用 ‎【例1】 (2014·全国Ⅰ卷)设D，E，F分别为△ABC的三边BC，CA，AB的中点，则＋＝(　　)‎ A. B. C. D. ‎【训练1】如图，已知＝a，＝b，＝3，用a，b表示，则＝________.‎ 考点二　平面向量的坐标运算 ‎【例2】 (1)已知向量a＝(5，2)，b＝(－4，－3)，c＝(x，y)，若3a－2b＋c＝0，则c＝(　　)‎ A.(－23，－12) B.(23，12)‎ C.(7，0) D.(－7，0)‎ ‎【训练2】 (1)已知点A(－1，5)和向量a＝(2，3)，若＝3a，则点B的坐标为(　　)‎ A.(7，4) B.(7，14)‎ C.(5，4) D.(5，14)‎ ‎(2)(2015·江苏卷)已知向量a＝(2，1)，b＝(1，－2).若ma＋nb＝(9，－8)(m，n∈R)，则m－n的值为________.‎ 考点三　平面向量共线的坐标表示 ‎【例3】 (1)已知平面向量a＝(1，2)，b＝(－2，m)，且a∥b，则2a＋3b＝________.‎ ‎(2)(必修4P101练习7改编)已知A(2，3)，B(4，－3)，点P在线段AB的延长线上，且|AP|＝|BP|，则点P的坐标为________.‎ ‎【训练3】 (1)(2017·浙江三市十二校联考)已知点A(1，3)，B(4，－1)，则与同方向的单位向量是(　　)‎ A. B. C. D. ‎(2)若三点A(1，－5)，B(a，－2)，C(－2，－1)共线，则实数a的值为________.‎ 第三部分　平面向量的数量积及其应用 ‎1.平面向量数量积的有关概念 ‎(1)向量的夹角：已知两个非零向量a和b，记＝a，＝b，则∠AOB＝θ(0°≤θ≤180°)叫做向量a与b的夹角.‎ ‎(2)数量积的定义：已知两个非零向量a与b，它们的夹角为θ，则数量|a||b|cos__θ 叫做a与b的数量积(或内积)，记作a·b，即a·b＝|a||b|cos__θ，规定零向量与任一向量的数量积为0，即0·a＝0.‎ ‎(3)数量积几何意义：数量积a·b等于a的长度|a|与b在a的方向上的投影|b|cosθ的乘积.‎ ‎2.平面向量数量积的性质及其坐标表示 设向量a＝(x1，y1)，b＝(x2，y2)，θ为向量a，b的夹角.‎ ‎(1)数量积：a·b＝|a||b|cos θ＝x1x2＋y1y2.‎ ‎(2)模：|a|＝＝.‎ ‎(3)夹角：cos θ＝＝.‎ ‎(4)两非零向量a⊥b的充要条件：a·b＝0⇔x1x2＋y1y2＝0.‎ ‎(5)|a·b|≤|a||b|(当且仅当a∥b时等号成立)⇔|x1x2＋y1y2|≤ ·.‎ ‎3.平面向量数量积的运算律：(1)a·b＝b·a(交换律).(2)λa·b＝λ(a·b)＝a·(λb)(结合律).(3)(a＋b)·c＝a·c＋b·c(分配律).‎ ‎【基础练习】‎ ‎1.(2015·全国Ⅱ卷)向量a＝(1，－1)，b＝(－1，2)，则(2a＋b)·a等于(　　)‎ A.－1 B.0 C.1 D.2‎ ‎2.(2017·湖州模拟)已知向量a，b，其中|a|＝，|b|＝2，且(a－b)⊥a，则向量a和b的夹角是________.‎ ‎3.(2016·石家庄模拟)已知平面向量a，b的夹角为，|a|＝2，|b|＝1，则|a＋b|＝________.‎ ‎5.(必修4P104例1改编)已知|a|＝5，|b|＝4，a与b的夹角θ＝120°，则向量b在向量a方向上的投影为________.‎ ‎6.(2017·瑞安一中检测)已知a，b，c是同一平面内的三个向量，其中a＝(1，2)，|b|＝1，且a＋b与a－2b垂直，则向量a·b＝________；a与b的夹角θ的余弦值为________.‎ ‎【考点突破】‎ 考点一　平面向量的数量积及在平面几何中的应用（用已知表示未知）‎ ‎【例1】 (1)(2015·四川卷)设四边形ABCD为平行四边形，||＝6，||＝4，若点M，N满足＝3，＝2，则·等于(　　)‎ A.20 B. 15 C.9 D.6‎ ‎(2)(2016·天津卷)已知△ABC是边长为1的等边三角形，点D，E分别是边AB，BC的中点，连接DE并延长到点F，使得DE＝2EF，则·的值为(　　)‎ A.－ B. C. D. ‎【训练1】 (1)(2017·义乌市调研)在Rt△ABC中，∠A＝90°，AB＝AC＝2，点D为AC的中点，点E满足＝，则·＝________.‎ ‎(2)(2017·宁波质检)已有正方形ABCD的边长为1，点E是AB边上的动点，则·的值为________；·的最大值为________.‎ 考点二　平面向量的夹角与垂直 ‎【例2】 (1)(2016·全国Ⅱ卷)已知向量a＝(1，m)，b＝(3，－2)，且(a＋b)⊥b，则m＝(　　)‎ A.－8 B.－6 C.6 D.8‎ ‎(2)若向量a＝(k，3)，b＝(1，4)，c＝(2，1)，已知2a－3b与c的夹角为钝角，则k的取值范围是________.‎ ‎【训练2】 (1)(2016·全国Ⅲ卷)已知向量＝，＝，则∠ABC＝(　　)‎ A.30° B.45° C.60° D.120°‎ ‎(2)(2016·全国Ⅰ卷)设向量a＝(m，1)，b＝(1，2)，且|a＋b|2＝|a|2＋|b|2，则m＝________.‎ 考点三　平面向量的模及其应用 ‎【例3】 (2017·云南统一检测)已知平面向量a与b的夹角等于，若|a|＝2，|b|＝3，则|2a ‎－3b|＝(　　)‎