高考数学试题的评价 萍乡中学Powered by 3页

‎2009年高考数学试题的评价 一．高考命题的可喜变化 ‎1. 体现新课标的理念，重视考查数学的科学价值、应用价值、文化价值，考查发现和提出问题、分析和解决问题的能力；增强了对应用意识、解决简单实际问题的能力的考查力度。‎ ‎2. 重视基础知识、基本技能、基本数学活动经验、基本数学思想的考查，重视对数学本质的理解水平的考查；在重视对演绎推理能力考查的同时，也开始关注对归纳推理能力的考查；注重把握数学学科特点，在知识与能力的结合、常规题与创新题的比例等方面做出很好的探索，很多试卷在知识结构、思想方法、能力层次等方面力求匹配合理。‎ ‎3．新课标试卷总体符合”课标实验版”高考考试大纲的要求．必修五个模块与选修Ⅰ、Ⅱ两个系列作为考查的主体，必修与选修内容的比率比较合理；突出了对高中数学重点知识的考查。注重通性通法的考查，淡化特殊技巧，关注考生对中学数学知识中所蕴涵的数学思想和方法的掌握程度；注重应用意识和创新意识的考查；强调了试题背景，阅读量加大，加强对阅读理解能力的考查；对新增内容，自始至终都坚持重点考查，考查的范围和深度逐年加大。‎ ‎4. 控制整卷难度，多数试卷难度稳定在0.55---0.65之间，很多考题，设计了坡度，题目难度逐阶递升，适应不同学生的学科学习特点，使不同的学生可以在不同难度层面上解答，给了每个考生展示自己数学学习水平的机会。‎ 二．高考数学试卷的亮点 今年高考数学试卷，总体上，立足基础，努力创新，拓展能力，追求发展，有许多亮点。感受较深的几点如下:‎ ‎1. 重视基础知识的考查 ‎2. 重视数学通性通法的考查 ‎3. 注重应用意识和创新意识的考查 ‎4. 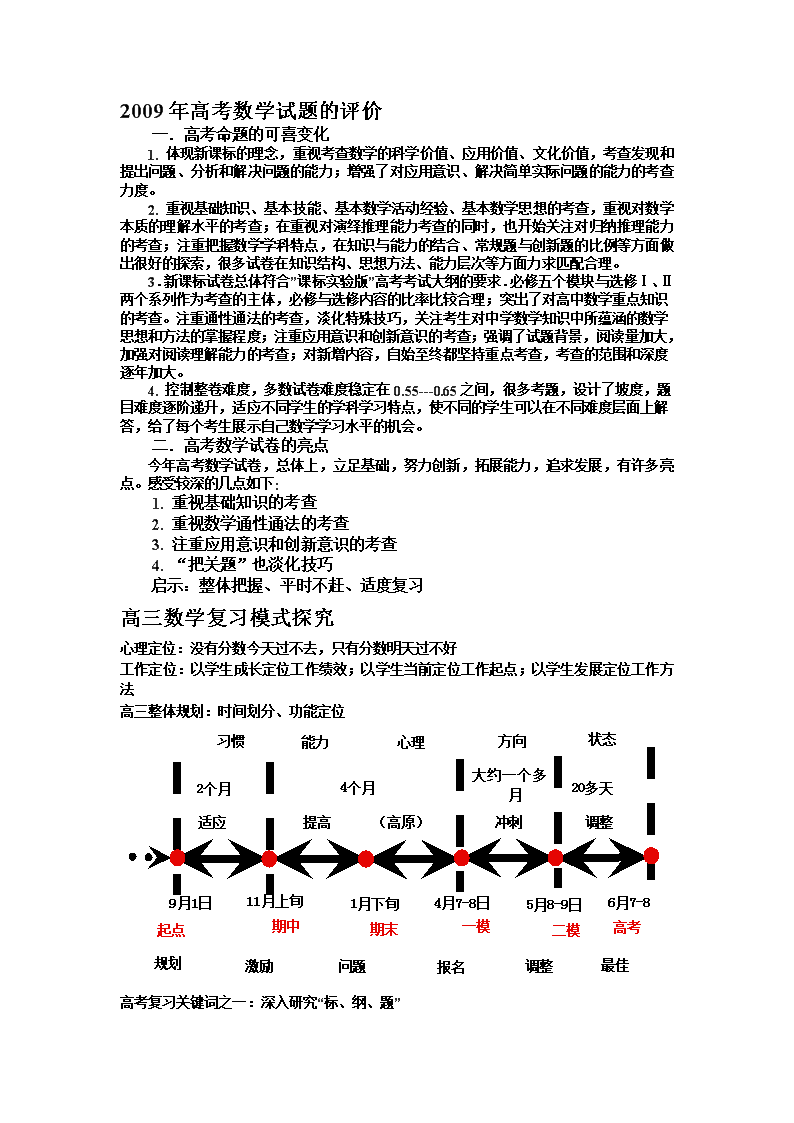“把关题”也淡化技巧 启示：整体把握、平时不赶、适度复习 高三数学复习模式探究 心理定位：没有分数今天过不去，只有分数明天过不好 工作定位：以学生成长定位工作绩效；以学生当前定位工作起点；以学生发展定位工作方法 高三整体规划：时间划分、功能定位 高考 一模 二模 期中 期末 起点 ‎11月上旬 ‎5月8-9日 ‎6月7-8‎ 提高 （高原） ‎ 冲刺 调整 ‎4月7-8日 适应 ‎4个月 大约一个多月 ‎20多天 ‎2个月 ‎1月下旬 习惯 能力 心理 方向 状态 ‎9月1日 问题 报名 调整 最佳 激励 规划 高考复习关键词之一：深入研究“标、纲、题”‎ • 标——课改新课标 • 纲——当年新考纲 • 题——近年高考题 高考复习关键词之二：激发学生、调动家长 不是推着走，而是主动跑 • 让学生着急 • 让家长紧张 • 让老师沉稳 • 数学学习——先紧后松 高考复习关键词之三：团结协助 • ‎“先讲后练”模式．即教师先从数学知识结构入手进行复习，顺藤摸瓜，各个击破，将要复习的知识点通过师生互动完整地梳理出来，然后进行例题讲解，最后是巩固性练习．其基本思路是：梳理知识——例题教学——学生练习——布置作业 高考复习关键词之四：精选例题与习题 选什么例题？怎么讲？‎ 从学生最擅长的方法入手 高考复习关键词之五：高效课堂 高考复习关键词之六：规范训练 高考复习关键词之七：反思提升 多管齐下提高学生数学能力 一、精心设计复习课 ‎1．紧扣教材、教学大纲和考试大纲，精心做好复习计划，编写好或选好相关的复习资料。‎ ‎2．加强集体备课，发挥群体优势。‎ ‎3．精心设计每一堂课，做到目的明确，重点突出，讲究效率。‎ ‎4．注意信息交流，了解最新考试动态，获取好的复习资料。‎ 二、提高课堂教学效率 ‎1．在高三复习课上教师除了精心实际课堂教学内容外，还要舍得挤时间给学生思考。‎ ‎2．要鼓励学生敢于思考、敢于质疑、勇于创新。‎ ‎3．教师要虚心向学生学习，做到教学相长。‎ 三、提高学生的审题能力 ‎1．审题时必须迅速地获取题目中提供的主要信息。‎ ‎2．通过审题必须迅速地将题中的文字语言转化为数学语言。‎ ‎3．通过审题要尽可能发现问题的实质，更好地寻求解题途径。‎ ‎4．在审题中要注意对数学语言的相互转译和规范表述。 ‎ 四、精选习题，不搞题海战术 ‎1．精选的习题要结合学生学习实际，有针对性。 ‎ ‎2．教师对给学生的练习要事先解答，优中选优。‎ ‎3．在复习和练习过程中，归纳知识要点，总结解题规律。‎ ‎4.帮助学生构建知识体系，记忆所学知识。‎ 五、试卷讲评做到有的放矢 ‎ 六、注意学生的非智力因素对复习的影响 ‎1．了解影响学生数学成绩提高的成因，有针对性地做好转化工作。‎ ‎2．重视并合理安排强化基础知识和基本技能的强化训练。‎ ‎3． 做好学生的心理疏导工作，合理安排各阶段的复习。‎ 数学解题常见错误成因分析与应对策略 ‎ 错误一：概念和公式数学特征不明 错误二：题型解法理解不到位 错误三：运算错误 错误四：遗漏条件不用 错误五：未挖掘隐含条件 错误六：直观代替论证 错误七：以偏概全 ‎ 错误八：充要条件运用不当 错误九：忽视分类讨论或分类不全 ‎ 错误十：策略性错误