高考数学立体几何试题汇编大题学生1 6页

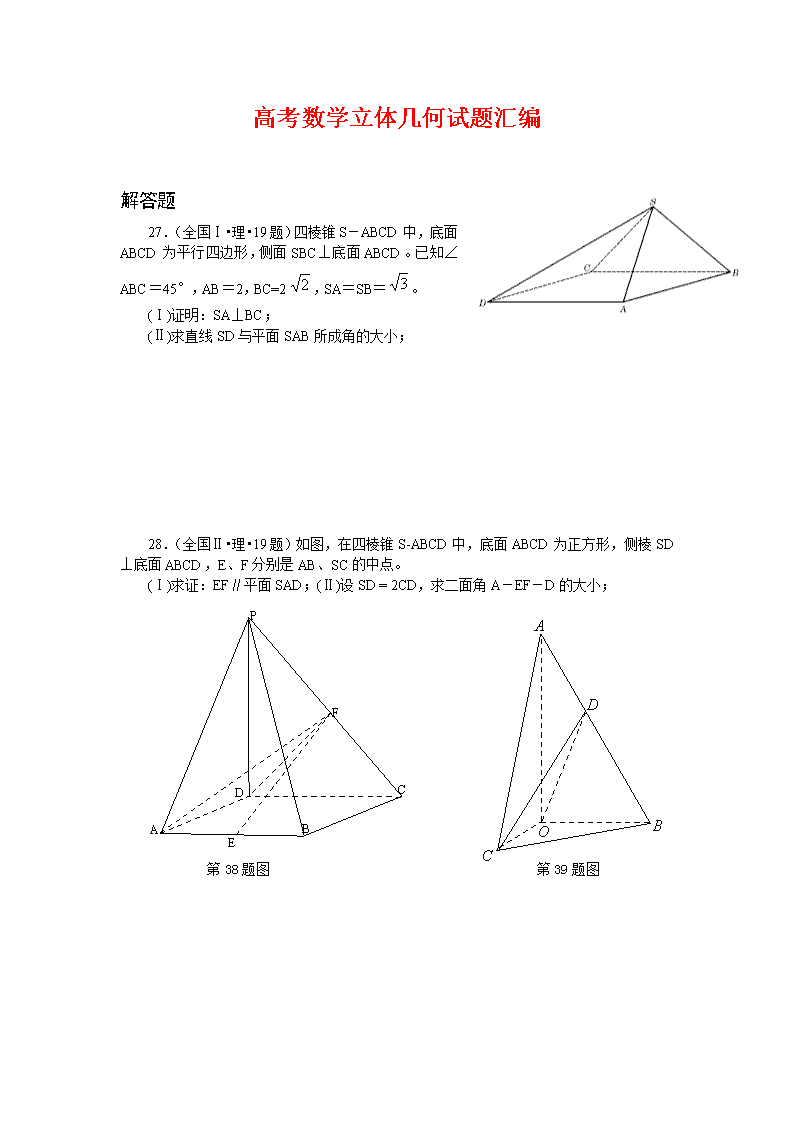
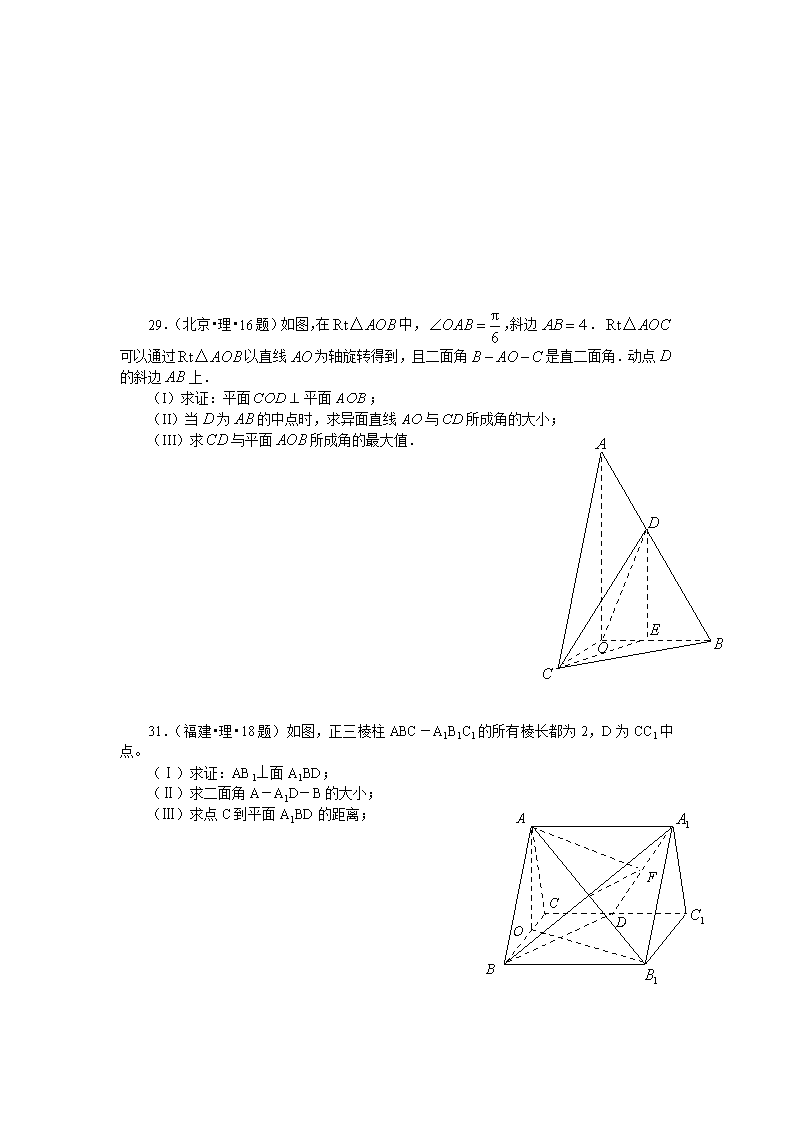
高考数学立体几何试题汇编 解答题 ‎27．（全国Ⅰ•理•19题）四棱锥S－ABCD中，底面ABCD为平行四边形，侧面SBC⊥底面ABCD。已知∠ABC＝45°，AB＝2，BC=2，SA＝SB＝。‎ ‎(Ⅰ)证明：SA⊥BC；‎ ‎(Ⅱ)求直线SD与平面SAB所成角的大小；‎ ‎28．（全国Ⅱ•理•19题）如图，在四棱锥S-ABCD中，底面ABCD为正方形，侧棱SD⊥底面ABCD，E、F分别是AB、SC的中点。‎ A B C D P E F 第38题图 第39题图 ‎(Ⅰ)求证：EF∥平面SAD；(Ⅱ)设SD = 2CD，求二面角A－EF－D的大小；‎ ‎29．（北京•理•16题）如图，在中，，斜边．可以通过以直线为轴旋转得到，且二面角是直二面角．动点的斜边上．‎ ‎（I）求证：平面平面；‎ ‎（II）当为的中点时，求异面直线与所成角的大小；‎ ‎（III）求与平面所成角的最大值．‎ ‎31．（福建•理•18题）如图，正三棱柱ABC－A1B1C1的所有棱长都为2，D为CC1中点。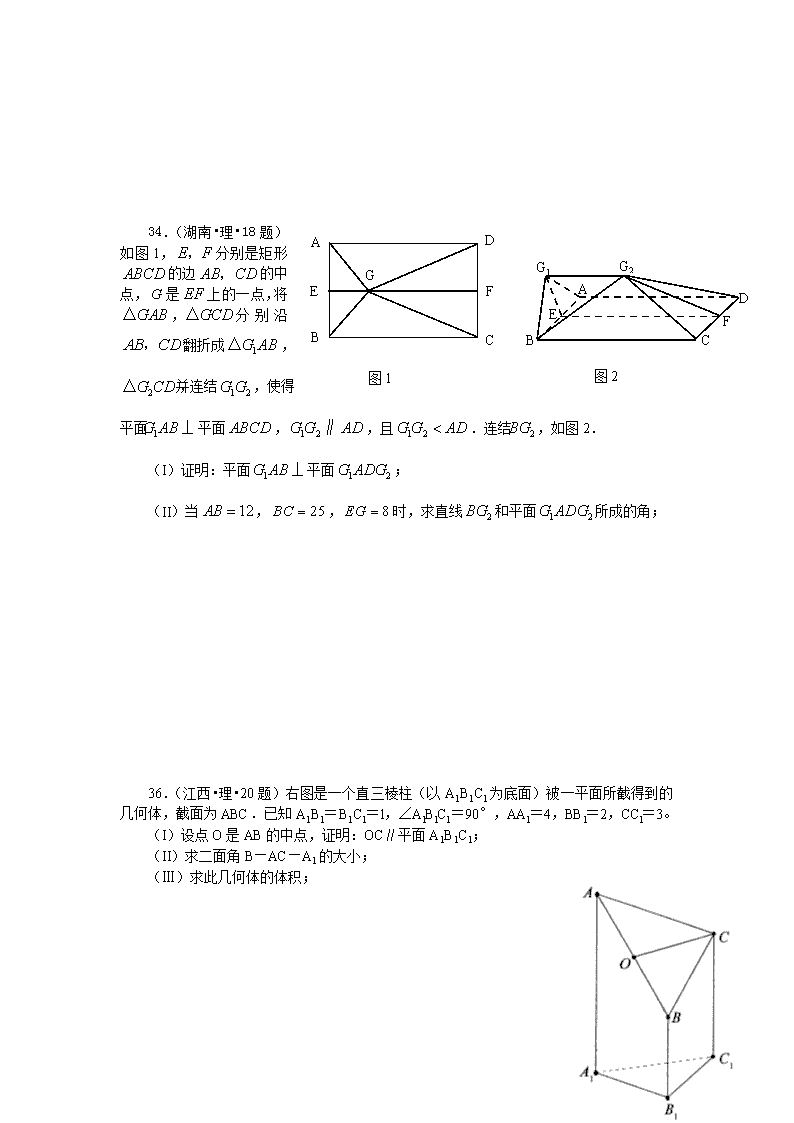‎ ‎（Ⅰ）求证：AB1⊥面A1BD；‎ ‎（Ⅱ）求二面角A－A1D－B的大小；‎ ‎（Ⅲ）求点C到平面A1BD的距离；‎A B C D O F A E B G D F C A E B C F D G1‎ G2‎ 图1‎ 图2‎ ‎34．（湖南•理•18题）如图1，分别是矩形的边的中点，是上的一点，将，分别沿翻折成，，并连结，使得平面平面，，且．连结，如图2． ‎ ‎（I）证明：平面平面；‎ ‎（II）当，，时，求直线和平面所成的角；‎ ‎36．（江西•理•20题）右图是一个直三棱柱（以A1B1C1为底面）被一平面所截得到的几何体，截面为ABC．已知A1B1＝B1C1＝l，∠AlBlC1＝90°，AAl＝4，BBl＝2，CCl＝3。‎ ‎（I）设点O是AB的中点，证明：OC∥平面A1B1C1；‎ ‎（II）求二面角B—AC—A1的大小；‎ ‎（Ⅲ）求此几何体的体积；‎ ‎38．（宁夏•理•19题）如图，在三棱锥中，侧面与侧面均为等边三角形，，为中点．‎ ‎（Ⅰ）证明：平面；（Ⅱ）求二面角的余弦值．‎ ‎39．（陕西•理•19题）如图,在底面为直角梯形的四棱锥中，，,BC=6。‎ ‎(Ⅰ)求证：；(Ⅱ)求二面角的大小；‎ ‎41．（四川•理•19题）如图，四边形是直角梯形，∠＝90°，∥，＝1，＝2，又＝1，∠＝120°，⊥，直线与直线所成的角为60°.‎ ‎（Ⅰ）求证：平面⊥平面；‎ ‎（Ⅱ）求二面角的大小；‎ ‎（Ⅲ）求三棱锥的体积；‎ ‎42．（天津•理•19题）如图，在四棱锥中，底面，，，是的中点．‎ ‎（Ⅰ）证明；‎ ‎（Ⅱ）证明平面；‎ ‎（Ⅲ）求二面角的大小；‎ ‎43．（浙江•理•19题）在如图所示的几何体中，平面ABC，平面ABC，，，M是AB的中点。‎ ‎（Ⅰ）求证：；‎ ‎（Ⅱ）求CM与平面CDE所成的角；‎