浙江高考理科数学试题逐题详解纯word解析版 11页

‎ 2014年浙江高考理科数学试题逐题详解 （纯word解析版）‎ 一、选择题：本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎【2014年浙江卷（理01）】设全集，集合，则 A. B. C. D.，‎ ‎【答案】B ‎【解析】全集U={x∈N|x≥2}，集合A={x∈N|x2≥5}={x∈N|x≥3}，则∁UA={x∈N|x＜3}={2}，故选：B ‎【2014年浙江卷（理02）】已知是虚数单位，、，则“”是“”的 A.充分不必要条件 B.必要不充分条件 C.充分必要条件 D.既不充分也不必要条件 ‎【答案】A ‎【解析】当“a=b=1”时，“（a+bi）2=（1+i）2=2i”成立，‎ 故“a=b=1”是“（a+bi）2=2i”的充分条件；‎ 当“（a+bi）2=a2﹣b2+2abi=2i”时，“a=b=1”或“a=b=﹣1”，‎ 故“a=b=1”是“（a+bi）2=2i”的不必要条件；‎ 综上所述，“a=b=1”是“（a+bi）2=2i”的充分不必要条件；‎ ‎【2014年浙江卷（理03）】某几何体的三视图（单位：）如图所示，则此几何体的表面积是 A.90 B.129 C.132 D.138‎ ‎【答案】D ‎【解析】由三视图知：几何体是直三棱柱与直四棱柱的组合体，其中直三棱柱的侧棱长为3，‎ 底面是直角边长分别为3、4的直角三角形，四棱柱的高为6，底面为矩形，矩形的两相邻边长为3和4，‎ ‎∴几何体的表面积S=2×4×6+3×6+3×3+2×3×4+2××3×4+（4+5）×3=48+18+9+24+12+27=138（cm2）．‎ ‎ ‎ ‎【2014年浙江卷（理04）】为了得到函数的图象，可以将函数的图象 A.向右平移个单位 B.向左平移个单位 C.向右平移个单位 D.向左平移个单位 ‎【答案】C ‎【解析】函数y=sin3x+cos3x=，故只需将函数y=cos3x的图象向右平移个单位，‎ 得到y==的图象．故选：C．‎ ‎【2014年浙江卷（理05）】在的展开式中，记项的系数为，，则，，，，‎ A.45 B.60 C.120 D.210‎ ‎【答案】C ‎【解析】（1+x）6（1+y）4的展开式中，含x3y0的系数是：=20．f（3，0）=20；‎ 含x2y1的系数是=60，f（2，1）=60；‎ 含x1y2的系数是=36，f（1，2）=36；‎ 含x0y3的系数是=4，f（0，3）=4；‎ ‎∴f（3，0）+f（2，1）+f（1，2）+f（0，3）=120．故选：C ‎【2014年浙江卷（理06）】已知函数，且，则 A. B. C. 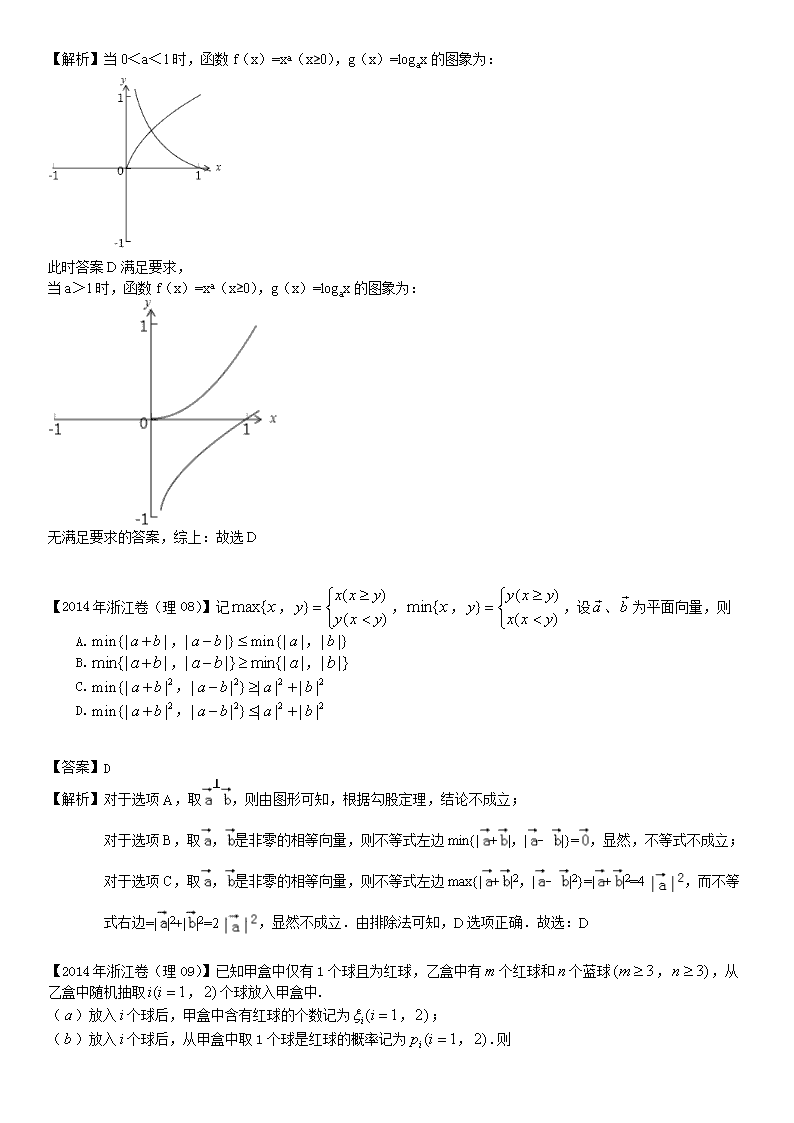D.‎ ‎【答案】C ‎【解析】由f（﹣1）=f（﹣2）=f（﹣3）得，解得，‎ f（x）=x3+6x2+11x+c，由0＜f（﹣1）≤3，得0＜﹣1+6﹣11+≤3，即6＜c≤9，故选C ‎【2014年浙江卷（理07）】在同一直角坐标系中，函数，的图象可能是 ‎【答案】D ‎【解析】当0＜a＜1时，函数f（x）=xa（x≥0），g（x）=logax的图象为：‎ 此时答案D满足要求，‎ 当a＞1时，函数f（x）=xa（x≥0），g（x）=logax的图象为：‎ 无满足要求的答案，综上：故选D ‎【2014年浙江卷（理08）】记，，，，设、为平面向量，则 A.，，‎ B.，，‎ C.，‎ D.，‎ ‎【答案】D ‎【解析】对于选项A，取⊥，则由图形可知，根据勾股定理，结论不成立；‎ 对于选项B，取，是非零的相等向量，则不等式左边min{|+|，|﹣|}=，显然，不等式不成立；‎ 对于选项C，取，是非零的相等向量，则不等式左边max{|+|2，|﹣|2}=|+|2=4，而不等 式右边=||2+||2=2，显然不成立．由排除法可知，D选项正确．故选：D ‎【2014年浙江卷（理09）】已知甲盒中仅有1个球且为红球，乙盒中有个红球和个蓝球，，从乙盒中随机抽取，个球放入甲盒中.‎ ‎（）放入个球后，甲盒中含有红球的个数记为，；‎ ‎（）放入个球后，从甲盒中取1个球是红球的概率记为，.则 A.， B.，‎ C.， D.，‎ ‎【答案】A ‎【解析】，，‎ ‎，所以P1＞P2；由已知ξ1的取值为1、2，ξ2的取值为1、2、3，‎ 所以 == ，E（ξ1）﹣E（ξ2）=．故选A ‎【2014年浙江卷（理10）】设函数，，，，，，，...，，记...，1，2，3，则 A. B.‎ C. D.‎ ‎【答案】B ‎【解析】由，故==1，‎ ‎ 由，故 ＜1，‎ ‎+ =，‎ 故I2＜I1＜I3，故选：B．‎ 二、填空题：本大题共7小题，每小题4分，共28分.‎ ‎【2014年浙江卷（理11）】若某程序框图如图所示，当输入50时，则该程序运算后输出的结果是________.‎ ‎【答案】6‎ ‎【解析】由程序框图知：第一次循环S=1，i=2；‎ ‎ 第二次循环S=2×1+2=4，i=3；‎ ‎ 第三次循环S=2×4+3=11，i=4；‎ ‎ 第四次循环S=2×11+4=26，i=5；‎ ‎ 第五次循环S=2×26+5=57，i=6，‎ ‎ 满足条件S＞50，跳出循环体，输出i=6．故答案为：6‎ ‎【2014年浙江卷（理12）】随机变量的取值为0，1，2，若，，则_____.‎ ‎【答案】‎ ‎【解析】设P（ξ=1）=p，P（ξ=2）=q，则由已知得p+q=，，解得，，‎ 所以．故答案为：‎ ‎【2014年浙江卷（理13）】当实数、满足时，恒成立，则实数的取值范围是________.‎ ‎【答案】‎ ‎【解析】由约束条件作可行域如图，‎ 联立，解得C（1，）．联立，解得B（2，1）．在x﹣y﹣1=0中取y=0得A（1，0）．‎ 要使1≤ax+y≤4恒成立，则，解得：1．∴实数a的取值范围是．故答案为：‎ ‎【2014年浙江卷（理14）】在8张奖券中有一、二、三等奖各1张，其余5张无奖.将这8张奖券分配给4个人，每人2张，不同的获奖情况有_____种（用数字作答）.‎ ‎【答案】60‎ ‎【解析】分类讨论，一、二、三等奖，三个人获得，共有=24种；‎ 一、二、三等奖，有1人获得2张，1人获得1张，共有=36种，‎ 共有24+36=60种．故答案为：60‎ ‎【2014年浙江卷（理15）】设函数，若，则实数的取值范围是______.‎ ‎【答案】（﹣∞，]‎ ‎【解析】∵函数f（x）=，它的图象如图所示：由 f（f（a））≤2，可得 f（a）≥﹣2．‎ 由f（x）=﹣2，可得﹣x2=﹣2，即x=，故当f（f（a））≤2时，则实数a的取值范围是a≤，‎ ‎ ‎ ‎ ‎ ‎【2014年浙江卷（理16）】设直线与双曲线两条渐近线分别交于点、，若点，满足，则该双曲线的离心率是__________.‎ ‎【答案】‎ ‎【解析】双曲线（a＞0，b＞0）的两条渐近线方程为y=±x，则 与直线x﹣3y+m=0联立，可得A（，），B（﹣，），‎ ‎∴AB中点坐标为（，），∵点P（m，0）满足|PA|=|PB|，‎ ‎∴=﹣3，∴a=2b，∴=b，∴e==．故答案为：‎ ‎【2014年浙江卷（理17）】如图，某人在垂直于水平地面的墙面前的点处进行射击训练.已知点 到墙面的距离为，某目标点沿墙面的射击线移动，此人为了准确瞄准目标点，需计算由点观察点的仰角的大小.若，，，则的最大值为____________.‎ ‎【答案】‎ ‎【解析】∵AB=15cm，AC=25cm，∠ABC=90°，∴BC=20cm，过P作PP′⊥BC，交BC于P′，连接AP′，则tanθ=，‎ 设BP′=x，则CP′=20﹣x，由∠BCM=30°，得PP′=CP′tan30°=（20﹣x），在直角△ABP′中，AP′=，‎ ‎∴tanθ=•，令y=，则函数在x∈[0，20]单调递减，∴x=0时，取得最大值为=．‎ 若P′在CB的延长线上，PP′=CP′tan30°=（20+x），在直角△ABP′中，AP′=，∴tanθ=•，‎ 令y=，则y′=0可得x=时，函数取得最大值，故答案为：‎ 三、解答题：本大题共5小题，共72分.解答应写出文字说明、证明过程或演算步骤.‎ ‎【2014年浙江卷（理18）】（本小题满分14分）‎ 在中，内角、、所对的边分别为、、，已知，，.‎ ⑴求角的大小；‎ ⑵若，求的面积.‎ 解：（Ⅰ）∵△ABC中，a≠b，c=，cos2A﹣cos2B=sinAcosA﹣sinBcosB，‎ ‎∴﹣=sin2A﹣sin2B，‎ 即 cos2A﹣cos2B=sin2A﹣sin2B，即﹣2sin（A+B）sin（A﹣B）=2•cos（A+B）sin（A﹣B）．‎ ‎∵a≠b，∴A≠B，sin（A﹣B）≠0，∴tan（A+B）=﹣，∴A+B=，∴C=．‎ ‎（Ⅱ）∵sinA=＜，C=，∴A＜，或A＞（舍去），∴cosA==．‎ 由正弦定理可得，=，即 =，∴a=．‎ ‎∴sinB=sin[（A+B）﹣A]=sin（A+B）cosA﹣cos（A+B）sinA=﹣（﹣）×=，‎ ‎∴△ABC的面积为 =×=‎ ‎【2014年浙江卷（理19）】（本小题满分14分）‎ 已知数列和满足.若为等比数列，且，.‎ ⑴求与；‎ ⑵设.记数列的前项和为.‎ ①求；‎ ②求正整数，使得对任意，均有.‎ 解：（Ⅰ）∵a1a2a3…an=（n∈N*） ①，当n≥2，n∈N*时， ②，‎ 由①②知：，令n=3，则有．∵b3=6+b2，∴a3=8．‎ ‎∵{an}为等比数列，且a1=2，∴{an}的公比为q，则=4，由题意知an＞0，∴q＞0，∴q=2．‎ ‎∴（n∈N*）．又由a1a2a3…an=（n∈N*）得：，‎ ‎，∴bn=n（n+1）（n∈N*）．‎ ‎（Ⅱ）（i）∵cn===．‎ ‎∴Sn=c1+c2+c3+…+cn==‎ ‎==；‎ ‎（ii）因为c1=0，c2＞0，c3＞0，c4＞0；当n≥5时，，‎ 而=＞0，得，‎ 所以，当n≥5时，cn＜0，综上，对任意n∈N*恒有S4≥Sn，故k=4‎ ‎【2014年浙江卷（理20）】（本小题满分15分）‎ 如图，在四棱锥中，平面平面，，，，.‎ ⑴证明：平面；‎ ⑵求二面角的大小.‎ 证明：（Ⅰ）在直角梯形BCDE中，由DE=BE=1，CD=2，得BD=BC=，由AC=，AB=2得AB2=AC2+BC2，即AC⊥BC，又平面ABC⊥平面BCDE，从而AC⊥平面BCDE，所以AC⊥DE，又DE⊥DC，从而DE⊥平面ACD；‎ 作BF⊥AD，与AD交于点F，过点F作FG∥DE，与AB交于点G，连接BG，由（Ⅰ）知DE⊥AD，则FG⊥AD，所以∠BFG就是二面角B﹣AD﹣E的平面角，在直角梯形BCDE中，由CD2=BC2+BD2，得BD⊥BC，‎ 又平面ABC⊥平面BCDE，得BD⊥平面ABC，从而BD⊥AB，由于AC⊥平面BCDE，得AC⊥CD．‎ 在Rt△ACD中，由DC=2，AC=，得AD=；‎ 在Rt△AED中，由ED=1，AD=得AE=；‎ 在Rt△ABD中，由BD=，AB=2，AD=得BF=，AF=AD，从而GF=，‎ 在△ABE，△ABG中，利用余弦定理分别可得cos∠BAE=，BC=．‎ 在△BFG中，cos∠BFG==，‎ 所以，∠BFG=，二面角B﹣AD﹣E的大小为 ‎【2014年浙江卷（理21）】(本小题满分15分)‎ 如图，设椭圆：，动直线与椭圆只有一个公共点，且点在第一象限.‎ ⑴已知直线的斜率为，用、、表示点的坐标；‎ ⑵若过原点的直线与垂直，证明：点到直线的距离的最大值为.‎ 解：（Ⅰ）设直线l的方程为y=kx+m（k＜0），由，消去y得 ‎（b2+a2k2）x2+2a2kmx+a2m2﹣a2b2=0．‎ 由于直线l与椭圆C只有一个公共点P，故△=0，即b2﹣m2+a2k2=0，解得点P的坐标为 ‎（﹣，），‎ 又点P在第一象限，故点P的坐标为P（，）．‎ ‎（Ⅱ）由于直线l1过原点O且与直线l垂直，故直线l1的方程为x+ky=0，所以点P到直线l1的距离 d=，‎ 整理得：d=，‎ 因为a2k2+≥2ab，所以≤=a﹣b，当且仅当k2=时等号成立．‎ 所以，点P到直线l1的距离的最大值为a﹣b ‎【2014年浙江卷（理22）】（本小题满分14分）‎ 已知函数.‎ ⑴若在，上的最大值和最小值分别记为、，求；‎ ⑵设，若对，恒成立，求的取值范围.‎ 解：（Ⅰ）∵f（x）=x3+3|x﹣a|=，‎ ‎∴f′（x）=，‎ ‎①a≤﹣1时，∵﹣1≤x≤1，∴x≥a，f（x）在（﹣1，1）上是增函数，‎ ‎∴M（a）=f（1）=4﹣3a，m（a）=f（﹣1）=﹣4﹣3a，‎ ‎∴M（a）﹣m（a）=8；‎ ‎②﹣1＜a＜1时，x∈（a，1），f（x）=x3+3x﹣3a，在（a，1）上是增函数；x∈（﹣1，a），f（x）=x3﹣3x﹣3a，在（﹣1，a）上是减函数，‎ ‎∴M（a）=max{f（1），f（﹣1）}，m（a）=f（a）=a3，‎ ‎∵f（1）﹣f（﹣1）=﹣6a+2，‎ ‎∴﹣1＜a≤时，M（a）﹣m（a）=﹣a3﹣3a+4；‎ ‎＜a＜1时，M（a）﹣m（a）=﹣a3+3a+2；‎ ‎③a≥1时，有x≤a，f（x）在（﹣1，1）上是减函数，‎ ‎∴M（a）=f（﹣1）=2+3a，m（a）=f（1）=﹣2+3a，‎ ‎∴M（a）﹣m（a）=4；‎ ‎（Ⅱ）令h（x）=f（x）+b，则h（x）=，h′（x）=，‎ ‎∵[f（x）+b]2≤4对x∈[﹣1，1]恒成立，‎ ‎∴﹣2≤h（x）≤2对x∈[﹣1，1]恒成立，‎ 由（Ⅰ）知，‎ ‎①a≤﹣1时，h（x）在（﹣1，1）上是增函数，最大值h（1）=4﹣3a+b，最小值h（﹣1）=﹣4﹣3a+b，则﹣4﹣3a+b≥﹣2且4﹣3a+b≤2矛盾；‎ ‎②﹣1＜a≤时，最小值h（a）=a3+b，最大值h（1）=4﹣3a+b，∴a3+b≥﹣2且4﹣3a+b≤2，‎ 令t（a）=﹣2﹣a3+3a，则t′（a）=3﹣3a2＞0，t（a）在（0，）上是增函数，∴t（a）＞t（0）=﹣2，‎ ‎∴﹣2≤3a+b≤0；‎ ‎③＜a＜1时，最小值h（a）=a3+b，最大值h（﹣1）=3a+b+2，则a3+b≥﹣2且3a+b+2≤2，∴﹣＜3a+b≤0；‎ ‎④a≥1时，最大值h（﹣1）=3a+b+2，最小值h（1）=3a+b﹣2，则3a+b﹣2≥﹣2且3a+b+2≤2，∴3a+b=0．‎ 综上，3a+b的取值范围是﹣2≤3a+b≤0．‎