高考数学分类汇编统计与概率 10页

www.gkstk.com ‎2016年高考数学试题分类汇编 统计与概率 一、选择题 ‎1、（2016年北京高考）从甲、乙等5名学生中随机选出2人，则甲被选中的概率为 ‎（A） （B） （C） （D） ‎ ‎【答案】B ‎2、（2016年北京高考）某学校运动会的立定跳远和30秒跳绳两个单项比赛分成预赛和决赛两个阶段.下表为10名学生的预赛成绩，其中有三个数据模糊.‎ 学生序号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 立定跳远（单位：米）‎ ‎1.96‎ ‎1.92‎ ‎1.82]‎ ‎1.80‎ ‎1.78‎ ‎1.76‎ ‎1.74‎ ‎1.72‎ ‎1.68‎ ‎1.60‎ ‎30秒跳绳（单位：次）‎ ‎63‎ a ‎75‎ ‎60‎ ‎63‎ ‎72‎ ‎70‎ a−1‎ b ‎65‎ 在这10名学生中，进入立定跳远决赛的有8人，同时进入立定跳远决赛和30秒跳绳决赛的有6人，则 ‎（A）2号学生进入30秒跳绳决赛 （B）5号学生进入30秒跳绳决赛 ‎ ‎（C）8号学生进入30秒跳绳决赛 （D）9号学生进入30秒跳绳决赛 ‎【答案】B ‎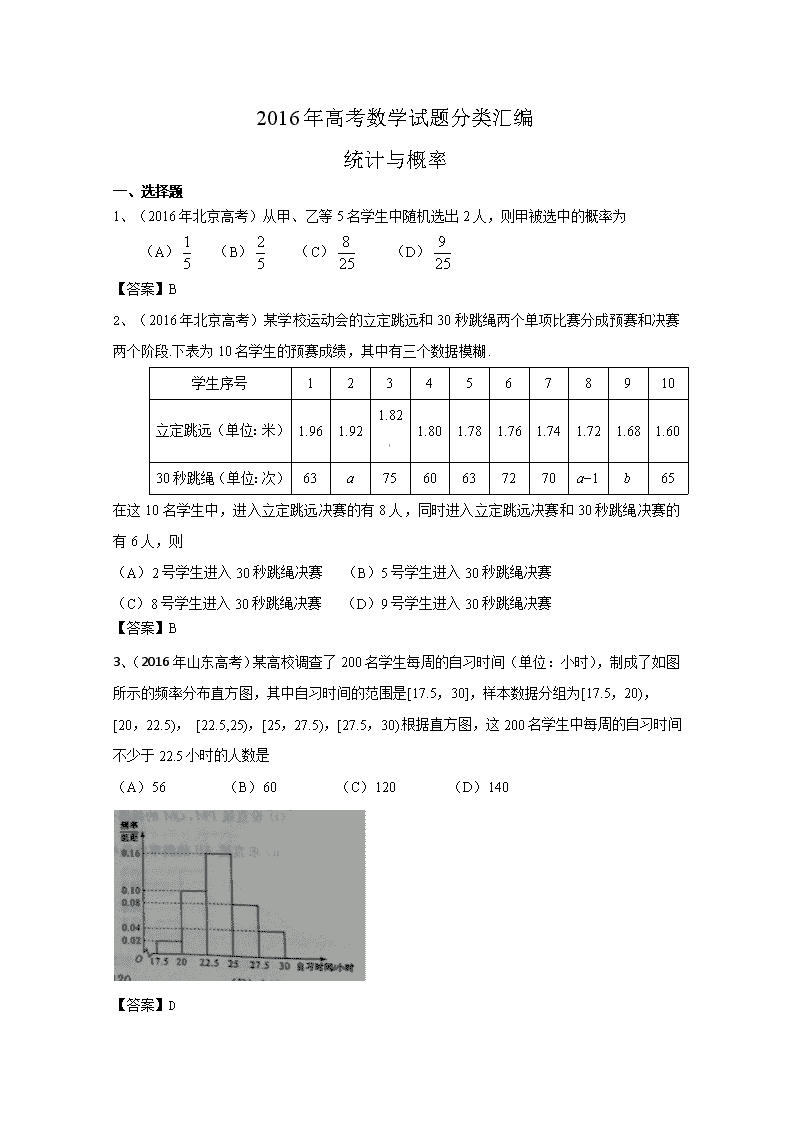3、（2016年山东高考）某高校调查了200名学生每周的自习时间（单位：小时），制成了如图所示的频率分布直方图，其中自习时间的范围是[17.5，30]，样本数据分组为[17.5，20)， [20，22.5)， [22.5,25)，[25，27.5)，[27.5，30).根据直方图，这200名学生中每周的自习时间不少于22.5小时的人数是 ‎（A）56 （B）60 （C）120 （D）140‎ ‎【答案】D ‎4、（2016年天津高考）甲、乙两人下棋，两人下成和棋的概率是，甲获胜的概率是，则甲不输的概率为 ‎（A） （B） （C） （D）‎ ‎【答案】A ‎5、（2016年全国I卷高考）为美化环境，从红、黄、白、紫4种颜色的花中任选2种花种在一个花坛中，余下的2种花种在另一个花坛中，则红色和紫色的花不在同一花坛的概率是 ‎（A）（B）（C）（D）‎ ‎【答案】C ‎6、（2016年全国II卷高考）某路口人行横道的信号灯为红灯和绿灯交替出现，红灯持续时间为40秒.若一名行人来到该路口遇到红灯，则至少需要等待15秒才出现绿灯的概率为（ ）‎ ‎（A） （B） （C） （D）‎ ‎【答案】B ‎7、（2016年全国III卷高考）某旅游城市为向游客介绍本地的气温情况，绘制了一年中月平均最高气温和平均最低气温的雷达图。图中A点表示十月的平均最高气温约为150C，B点表示四月的平均最低气温约为50C。下面叙述不正确的是 ‎(A) 各月的平均最低气温都在00C以上 (B) 七月的平均温差比一月的平均温差大 ‎(C) 三月和十一月的平均最高气温基本相同 (D) 平均气温高于200C的月份有5个 ‎【答案】D[‎ ‎8、（2016年全国III卷高考）小敏打开计算机时，忘记了开机密码的前两位，只记得第一位是中的一个字母，第二位是1,2,3,4,5‎ 中的一个数字，则小敏输入一次密码能够成功开机的概率是 ‎（A） （B） （C） （D） ‎ ‎【答案】C 二、填空题 ‎1、（2016年北京高考）某网店统计了连续三天售出商品的种类情况：第一天售出19种商品，第二天售出13种商品，第三天售出18种商品；前两天都售出的商品有3种，后两天都售出的商品有4种，则该网店 ‎①第一天售出但第二天未售出的商品有______种；‎ ‎②这三天售出的商品最少有_______种.‎ ‎【答案】①16；②29 ‎ ‎2、（2016年江苏省高考）已知一组数据4.7,4.8,5.1,5.4,5.5，则该组数据的方差是________▲_____. ‎ ‎【答案】0.1‎ ‎3、（2016年江苏省高考）将一颗质地均匀的骰子（一种各个面上分别标有1，2，3，4，5，6个点的正方体玩具）先后抛掷2次，则出现向上的点数之和小于10的概率是 ▲ .‎ ‎【答案】‎ ‎4、（2016年上海高考）某次体检，6位同学的身高（单位：米）分别为1.72,1.78,1.75,1.80,1.69,1.77则这组数据的中位数是_________（米）‎ ‎【答案】1.76‎ 三、解答题 ‎1、（2016年北京高考）某市民用水拟实行阶梯水价，每人用水量中不超过w立方米的部分按4元/立方米收费，超出w立方米的部分按10元/立方米收费，从该市随机调查了10000位居民，获得了他们某月的用水量数据，整理得到如下频率分布直方图：‎ ‎（I）如果w为整数，那么根据此次调查，为使80%以上居民在该月的用水价格为4元/立方米，w至少定为多少？‎ ‎（II）假设同组中的每个数据用该组区间的右端点值代替，当w=3时，估计该市居民该月的人均水费.‎ 解：（I）由用水量的频率分布直方图知，‎ 该市居民该月用水量在区间，，，，内的频 率依次为，，，，．‎ 所以该月用水量不超过立方米的居民占%，用水量不超过立方米的居民占%．‎ 依题意，至少定为．‎ ‎（II）由用水量的频率分布直方图及题意，得居民该月用水费用的数据分组与频率分布表：‎ 组号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ 分组 频率 根据题意，该市居民该月的人均水费估计为：‎ ‎（元）．‎ ‎2、（2016年山东高考）某儿童乐园在“六一”儿童节退出了一项趣味活动.参加活动的儿童需转动如图所示的转盘两次，每次转动后，待转盘停止转动时，记录指针所指区域中的数.设两次记录的数分别为x，y.奖励规则如下：‎ ‎①若，则奖励玩具一个；‎ ‎②若，则奖励水杯一个；‎ ‎③其余情况奖励饮料一瓶.‎ 假设转盘质地均匀，四个区域划分均匀.小亮准备参加此项活动.‎ ‎（I）求小亮获得玩具的概率；‎ ‎（II）请比较小亮获得水杯与获得饮料的概率的大小，并说明理由.‎ 解析：用数对表示儿童参加活动先后记录的数，则基本事件空间与点集一一对应.因为中元素个数是所以基本事件总数为 ‎（）记“”为事件.‎ 则事件包含的基本事件共有个，即 ‎ 所以，即小亮获得玩具的概率为.‎ ‎（）记“”为事件，“”为事件.‎ 则事件包含的基本事件共有个，即 所以，‎ 则事件包含的基本事件共有个，即 所以，‎ 因为 所以，小亮获得水杯的概率大于获得饮料的概率.‎ ‎4、（2016年上海高考）我国是世界上严重缺水的国家，某市为了制定合理的节水方案，对居民用水情况进行了调查，通过抽样，获得了某年100位居民每人的月均用水量（单位：吨），将数据按照[0,0.5）， [0.5,1），……[4,4.5]分成9组，制成了如图所示的频率分布直方图。‎ ‎（I）求直方图中的a值；‎ ‎（II）设该市有30万居民，估计全市居民中月均用水量不低于3吨的人数．说明理由；‎ ‎（Ⅲ）估计居民月均用水量的中位数。‎ ‎【解析】（Ⅰ）由频率分布直方图，可知：月用水量在[0,0.5]的频率为0.08×0.5=0.04.‎ 同理，在[0.5,1)，(1.5,2]，[2,2.5)，[3,3.5)，[3.5,4)，[4,4.5)等组的频率分别为0.08，0.21，0.25,0.06，0.04，0.02.‎ 由1–(0.04+0.08+0.21+.025+0.06+0.04+0.02)=0.5×a+0.5×a，‎ 解得a=0.30.‎ ‎（Ⅱ）由（Ⅰ），100位居民月均水量不低于3吨的频率为0.06+0.04+0.02=0.12.‎ 由以上样本的频率分布，可以估计30万居民中月均用水量不低于3吨的人数为300000×0.13=36000.‎ ‎（Ⅲ）设中位数为x吨.‎ 因为前5组的频率之和为0.04+0.08+0.15+0.21+0.25=0.73>0.5，‎ 而前4组的频率之和为0.04+0.08+0.15+0.21=0.48<0.5‎ 所以2≤x<2.5.‎ 由0.50×（x–2）=0.5–0.48，解得x=2.04.‎ 故可估计居民月均用水量的中位数为2.04吨.‎ ‎5、（2016年全国I卷高考）某公司计划购买1台机器，该种机器使用三年后即被淘汰.机器有一易损零件，在购进机器时，可以额外购买这种零件作为备件，每个200元.在机器使用期间，如果备件不足再购买，则每个500元.现需决策在购买机器时应同时购买几个易损零件，为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数，得下面柱状图：‎ 记x表示1台机器在三年使用期内需更换的易损零件数，y表示1台机器在购买易损零件上所需的费用（单位：元），表示购机的同时购买的易损零件数.‎ ‎（I）若=19，求y与x的函数解析式；‎ ‎（II）若要求“需更换的易损零件数不大于”的频率不小于0.5，求的最小值；‎ ‎（III）假设这100台机器在购机的同时每台都购买19个易损零件，或每台都购买20个易损零件，分别计算这100台机器在购买易损零件上所需费用的平均数，以此作为决策依据，购买1台机器的同时应购买19个还是20个易损零件？‎ ‎（Ⅱ）由柱状图知，需更换的零件数不大于18的频率为0.46，不大于19的频率为0.7，故的最小值为19.‎ ‎（Ⅲ）若每台机器在购机同时都购买19个易损零件，则这100台机器中有70台在购买易损零件上的费用为3800，20台的费用为4300，10台的费用为4800，因此这100台机器在购买易损零件上所需费用的平均数为.‎ 若每台机器在购机同时都购买20个易损零件，则这100台机器中有90台在购买易损零件上的费用为4000，10台的费用为4500，因此这100台机器在购买易损零件上所需费用的平均数为.‎ 比较两个平均数可知，购买1台机器的同时应购买19个易损零件.‎ ‎6、（2016年全国II卷高考）某险种的基本保费为（单位：元），继续购买该险种的投保人称为续保人，续保人本年度的保费与其 上年度出险次数的关联如下：‎ 上年度出险次数 ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ 保费 随机调查了该险种的200名续保人在一年内的出险情况，得到如下统计表：‎ 出险次数 ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ 频数 ‎60‎ ‎50‎ ‎30‎ ‎30‎ ‎20‎ ‎10‎ ‎（Ⅰ）记A为事件：“一续保人本年度的保费不高于基本保费”.求的估计值；‎ ‎（Ⅱ）记B为事件：“一续保人本年度的保费高于基本保费但不高于基本保费的160％”.‎ 求的估计值；‎ ‎（III）求续保人本年度的平均保费估计值.‎ 解析：（Ⅰ）事件A发生当且仅当一年内出险次数小于2.由所给数据知，一年内险次数小于2的频率为，‎ 故P(A)的估计值为0.55.‎ ‎（Ⅱ）事件B发生当且仅当一年内出险次数大于1且小于4.由是给数据知，一年内出险次数大于1且小于4的频率为，‎ 故P(B)的估计值为0.3.‎ ‎(Ⅲ)由题所求分布列为：‎ 保费 ‎0.85a a ‎1.25a ‎1.5a ‎1.75a ‎2a 频率 ‎0.30‎ ‎0.25‎ ‎0.15‎ ‎0.15‎ ‎0.10‎ ‎0.05‎ 调查200名续保人的平均保费为 ‎，‎ 因此，续保人本年度平均保费估计值为1.1925a.‎ ‎9、（2016年全国III卷高考）‎ 下图是我国2008年至2014年生活垃圾无害化处理量（单位：亿吨）的折线图 ‎（Ⅰ）由折线图看出，可用线性回归模型拟合y与t的关系，请用相关系数加以说明；‎ ‎（Ⅱ）建立y关于t的回归方程（系数精确到0.01），预测2016年我国生活垃圾无害化处理量.‎ 附注：‎ 参考数据：，，，≈2.646.‎ 参考公式：相关系数 ‎ 回归方程 中斜率和截距的最小二乘估计公式分别为：‎ ‎（Ⅱ）由及（Ⅰ）得，‎ 所以，关于的回归方程为：. ..........10分 将2016年对应的代入回归方程得：.‎ 所以预测2016年我国生活垃圾无害化处理量将约1.82亿吨. .........12分