高考数学理基础知识总复习课时精练空间简单几何体的表面积和体积高考 7页

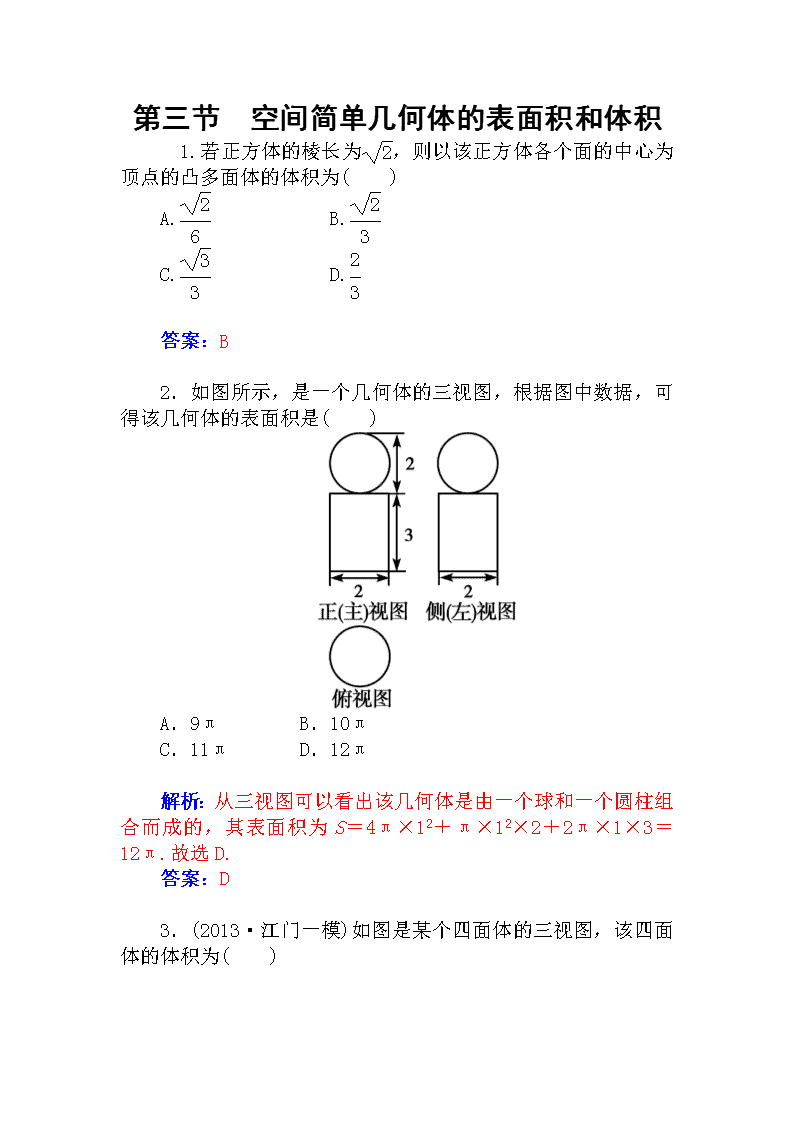
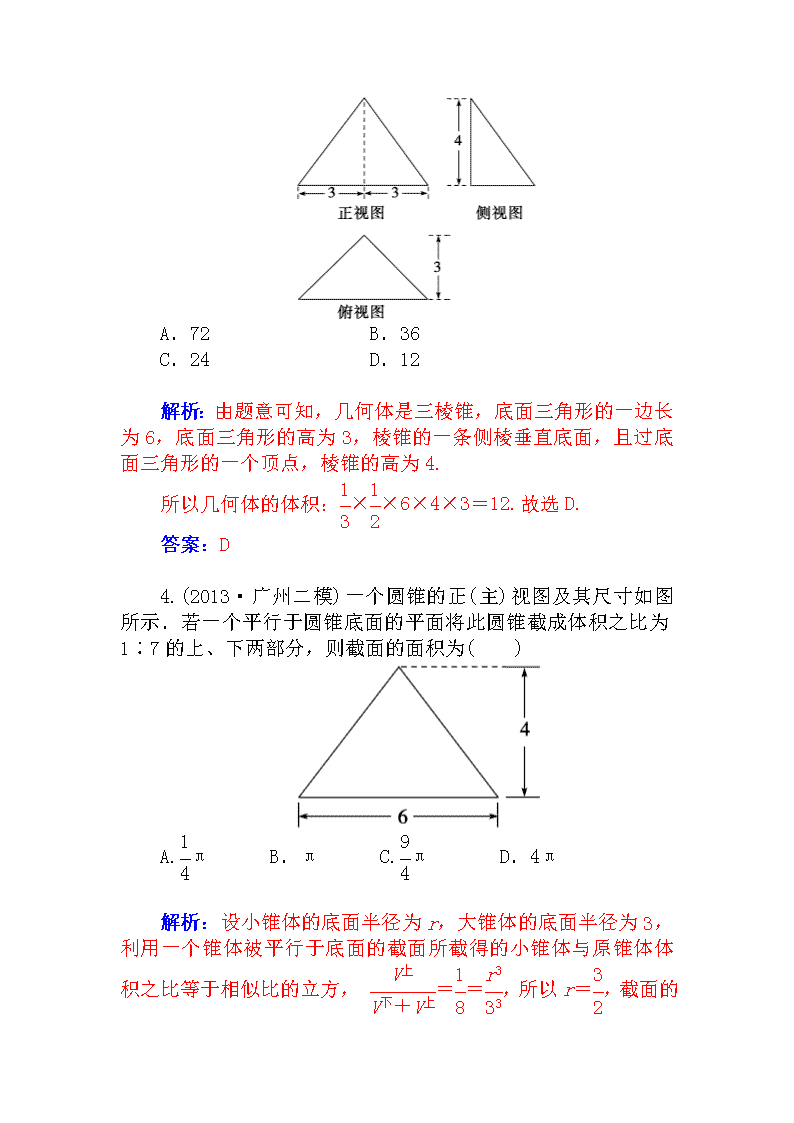
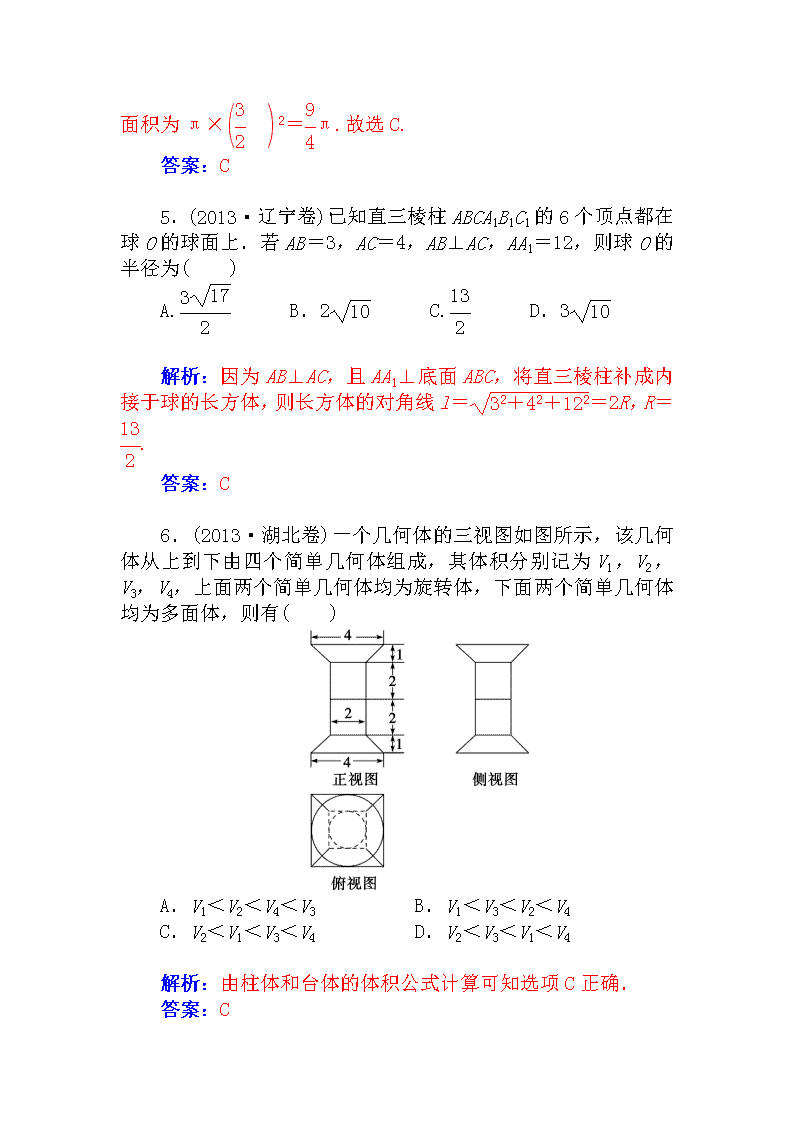
第三节　空间简单几何体的表面积和体积 ‎　1.若正方体的棱长为，则以该正方体各个面的中心为顶点的凸多面体的体积为(　　)‎ A. B. C. D. 答案：B ‎2．如图所示，是一个几何体的三视图，根据图中数据，可得该几何体的表面积是(　　) ‎ A．9π B．10π C．11π D．12π 解析：从三视图可以看出该几何体是由一个球和一个圆柱组合而成的，其表面积为S＝4π×12＋π×12×2＋2π×1×3＝12π.故选D.‎ 答案：D ‎ ‎　　　‎ ‎3．(2013·江门一模)如图是某个四面体的三视图，该四面体的体积为(　　) ‎ A．72 B．36‎ C．24 D．12‎ 解析：由题意可知，几何体是三棱锥，底面三角形的一边长为6，底面三角形的高为3，棱锥的一条侧棱垂直底面，且过底面三角形的一个顶点，棱锥的高为4.‎ 所以几何体的体积：××6×4×3＝12.故选D.‎ 答案：D ‎4.(2013·广州二模)一个圆锥的正(主)视图及其尺寸如图所示．若一个平行于圆锥底面的平面将此圆锥截成体积之比为1∶7的上、下两部分，则截面的面积为(　　) ‎ A.π B．π C.π D．4π 解析：设小锥体的底面半径为r，大锥体的底面半径为3，利用一个锥体被平行于底面的截面所截得的小锥体与原锥体体积之比等于相似比的立方， ＝＝，所以r＝ ‎，截面的面积为π×2＝π.故选C.‎ 答案：C ‎5．(2013·辽宁卷)已知直三棱柱ABCA1B‎1C1的6个顶点都在球O的球面上．若AB＝3，AC＝4，AB⊥AC，AA1＝12，则球O的半径为(　　)‎ A. B．2 C. D．3 解析：因为AB⊥AC，且AA1⊥底面ABC，将直三棱柱补成内接于球的长方体，则长方体的对角线l＝＝2R，R＝.‎ 答案：C ‎6．(2013·湖北卷)一个几何体的三视图如图所示，该几何体从上到下由四个简单几何体组成，其体积分别记为V1，V2，V3，V4，上面两个简单几何体均为旋转体，下面两个简单几何体均为多面体，则有(　　)‎ A．V1＜V2＜V4＜V3 B．V1＜V3＜V2＜V4‎ C．V2＜V1＜V3＜V4 D．V2＜V3＜V1＜V4‎ 解析：由柱体和台体的体积公式计算可知选项C正确．‎ 答案：C ‎7．(2013·佛山一模)一个直棱柱被一平面截去一部分所得几何体的三视图如下，则几何体的体积为(　　)‎ A．8 B．9 C．10 D．11‎ 解析：三视图复原的几何体是底面边长为2的正方形，棱长垂直底面的四棱柱，其高为3，从该四棱柱中去掉一个三棱锥，该三棱锥的底面是面积为×2×1＝1的直角三角形，高为3，所以几何体的体积是：2×2×3－×3××2×1＝11，故选D.‎ 答案：D ‎8．若一个圆锥的侧面展开图是面积为2π的半圆面，则该圆锥的体积为__________．‎ 解析：因为半圆面的面积为πl2＝2π，所以l2＝4，即l＝2，即圆锥的母线为l＝2，底面圆的周长2πr＝πl＝2π，所以圆锥的底面半径r＝1，所以圆锥的高h＝＝，所以圆锥的体积为πr2h＝π×＝.‎ 答案： ‎9.(2013·江苏卷)如图，在三棱柱A1B‎1C1ABC中，D，E，F分别是AB，AC，AA1的中点，设三棱锥FADE的体积为V1，三棱柱A1B‎1C1ABC的体积为V2，则V1V2＝________.‎ 解析：V1＝S△ADEh1＝×S△ABC×h2＝V2，所以V1V2＝.‎ 答案： ‎10．如图所示，已知一个半径为1的半球形容器①及容器②的三视图，侧视图矩形的宽为5，俯视图是边长为1的正三角形．‎ ‎(1)请画出容器②的直观图(简图，尺寸不作严格要求)，并回答：它是什么几何体？‎ ‎(2)若把容器①中盛满的水全部注入容器②中，水是否会从容器②中溢出？为什么？(参考数据：≈1.732)‎ 解析：(1)容器②的直观图如右图所示，它是正三棱柱．‎ ‎(2)∵V半球＝×π×13＝≈2.094，‎ V三棱柱＝Sh＝≈2.165.‎ ‎∴V半球＜V三棱柱，∴水不会从三棱柱容器里溢出．‎ ‎11．如图，在直角梯形ABCD中，∠ADC＝90°，CD∥AB，AB＝4，AD＝CD＝2，将△ADC沿AC折起，使平面ADC⊥平面ABC，得到几何体DABC，如图所示．‎ ‎(1)求证：BC⊥平面ACD；‎ ‎(2)求几何体DABC的体积．‎ ‎(1)证明：在平面图中，可得AC＝BC＝2，‎ 从而AC2＋BC2＝AB2，故AC⊥BC.‎ 取AC的中点O，连接DO，则DO⊥AC.‎ 又平面ADC⊥平面ABC，‎ 平面ADC∩平面ABC＝AC，DO⊂平面ADC，‎ 从而DO⊥平面ABC，∴DO⊥BC.‎ 又AC⊥BC，AC∩DO＝O，‎ ‎∴BC⊥平面ACD.‎ ‎(2)解析：由(1)可知BC为三棱锥BACD的高，BC＝2，S△ACD＝2，‎ ‎∴VBACD＝S△ACD·BC＝×2×2＝，‎ 由等体积性可知，几何体DABC的体积为.‎