问题探究型—高考数学创新题型之赏析 6页

四、问题探究型 问题探究型创新题形式多、难度大，在解答时要通过分析、探究，抓住有限的或隐含的条件，通过联想综合性的知识设计出解决问题的方式或探究出解决问题的数学思想，是考查学生数学素养和应用能力的主要和重要题型。纵观近几年高考，这类问题具体有三种题型：存在性探究问题、设计型探究问题以及公式推导型探究问题。‎ 存在性探究问题 ‎（08年江苏）18、设平面直角坐标系中，设二次函数的图象与坐标轴有三个交点，经过这三个交点的圆记为C。‎ （1） 求实数的取值范围；‎ （2） 求圆的方程；‎ （3） 问圆是否经过某定点（其坐标与无关）？请证明你的结论。‎ 解析 点评 本题属于存在性探究型创新题，由于解题方向不明，自由度大，故能很好考查考生的应变能力、思维能力和创新意识，体现新课程改革精神。‎ ‎（08广东文）11、这个题目综合考察了圆锥曲线。通过一个共同的参数b，联系了椭圆和抛物线。第二问最具创新性，综合考察了学生的数形结合能力。‎ ‎ 20.设，椭圆方程为， 抛物线方程为如图6所示，过点作轴的平行线，与抛物线在第一象限的交点为G，已知抛物线在点G的切线经过椭圆的右焦点。‎ ‎（1）求满足条件的椭圆方程和抛物线方程；‎ ‎（2）设A，B分别是椭圆长轴的左、右端点，试探究 在抛物线上是否存在点P,使得为直角三角形？若存在，请指出共有几个这样的点？并说明理由（不必具体求出这些点的坐标）。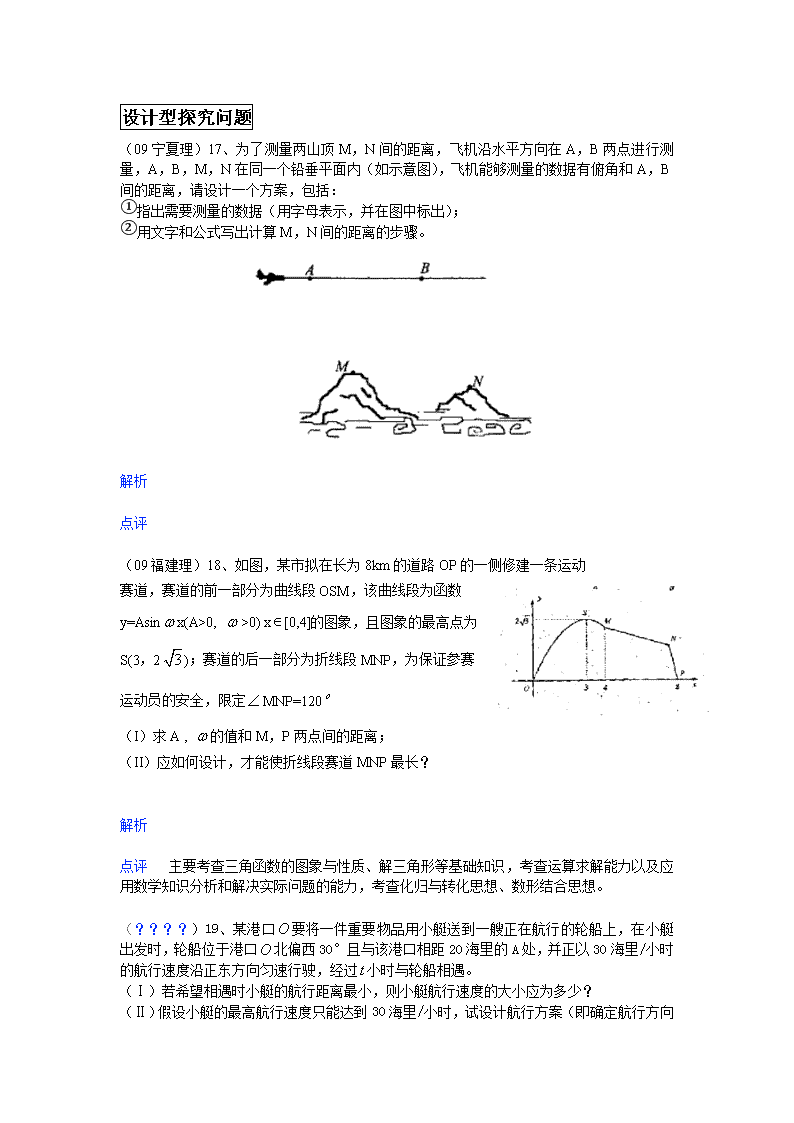（存在性探究问题）‎ 解析 点评 设计型探究问题 ‎（09宁夏理）17、为了测量两山顶M，N间的距离，飞机沿水平方向在A，B两点进行测量，A，B，M，N在同一个铅垂平面内（如示意图），飞机能够测量的数据有俯角和A，B间的距离，请设计一个方案，包括：‎ ‎①指出需要测量的数据（用字母表示，并在图中标出）；‎ ‎②用文字和公式写出计算M，N间的距离的步骤。‎ 解析 点评 ‎（09福建理）18、如图，某市拟在长为8km的道路OP的一侧修建一条运动 赛道，赛道的前一部分为曲线段OSM，该曲线段为函数 y=Asinx(A>0, >0) x[0,4]的图象，且图象的最高点为 S(3，2)；赛道的后一部分为折线段MNP，为保证参赛 运动员的安全，限定MNP=120‎ ‎（I）求A , 的值和M，P两点间的距离；‎ ‎（II）应如何设计，才能使折线段赛道MNP最长？ w.w.w.k.s.5.u.c 解析 点评 主要考查三角函数的图象与性质、解三角形等基础知识，考查运算求解能力以及应用数学知识分析和解决实际问题的能力，考查化归与转化思想、数形结合思想。‎ ‎（？？？？）19、某港口要将一件重要物品用小艇送到一艘正在航行的轮船上，在小艇出发时，轮船位于港口北偏西30°且与该港口相距20海里的A处，并正以30海里/小时的航行速度沿正东方向匀速行驶，经过小时与轮船相遇。‎ ‎（Ⅰ）若希望相遇时小艇的航行距离最小，则小艇航行速度的大小应为多少？‎ ‎（Ⅱ ‎）假设小艇的最高航行速度只能达到30海里/小时，试设计航行方案（即确定航行方向和航行速度的大小），使得小艇能以最短时间与轮船相遇，并说明理由。‎ 解析 ‎ 解法一：‎ ‎（I）设相遇时小艇航行的距离为S海里，则 ‎ ‎ ‎ =‎ ‎ =‎ ‎ 故当时，，此时 ‎ 即，小艇以海里/小时的速度航行，相遇时小艇的航行距离最小。‎ ‎ （II）设小艇与轮船在B出相遇，则K^S*5U.C#O ‎ ‎ ‎ 故 ‎ ，‎ ‎ 即，解得 ‎ 又时，‎ ‎ 故时，t取最小值，且最小值等于 ‎ 此时，在中，有，故可设计寒星方案如下：‎ ‎ 航行方向为北偏东，航行速度为30海里/小时，小艇能以最短时间与轮船相遇 解法二：‎ ‎（I）若相遇时小艇的航行距离最小，又轮船沿正东方向匀速行驶，则小艇航行方向为正北方向。‎ ‎ 设小艇与轮船在C处相遇。‎ ‎ 在中，，‎ ‎ 又， ‎ ‎ 此时，轮船航行时间，‎ ‎ 即，小艇以海里/小时的速度航行，相遇时小艇的航行距离最小。‎ ‎（II）猜想时，小艇能以最短时间与轮船在D出相遇，此时 ‎ 又，所以，解得 ‎ 据此可设计航行方案如下：‎ ‎ 航行方向为北偏东，航行速度为30海里/小时，小艇能以最短时间与轮船相遇 ‎ 证明如下：K^S*5U.C#O ‎ 如图，由（I）得，，‎ ‎ 故，且对于线段上任意点P，‎ ‎ 有 而小艇的最高航行速度只能达到30海里/小时，‎ ‎ 故小艇与轮船不可能在A，C之间（包含C）的任意位置相遇。‎ ‎ 设，则在中，，‎ ‎ 由于从出发到相遇，轮船与小艇所需要的时间分别为 ‎ 和 ‎ 所以，‎ ‎ 由此可得，‎ ‎ 又，故 ‎ 从而，‎ ‎ 由于时，取得最小值，且最小值为 ‎ 于是，当时，取得最小值，且最小值为 解法三：‎ ‎（I）同解法一或解法二 ‎（II）设小艇与轮船在B处相遇。依据题意得：K^S*5U.C#O ‎ ，‎ ‎ （‎ （1） 若，则由 ‎ =‎ 得 从而，，‎ ① 当时，‎ 令，则，，当且仅当即时等号成立。K^S*5U.C#O ②当时，同理可得 由①、②得，当时，‎ （2） 若，则 综合（1）、（2）可知，当时，t取最小值，且最小值等于 此时，在中，，故可设计航行方案如下：‎ 航行方向为北偏东，航行速度为30海里/小时，小艇能以最短时间与轮船相遇。‎ 点评 本小题主要考查解三角形、二次函数等基础知识，考查函数与方程思想、数形结合思想、化归与转化思想、分类与整合思想。‎ 推导型探究题 此类题型考查的内容一般是将公式由特殊向一般情况的推导，也可能是公式或者是定理应用范围的推广等 ‎（10江苏理）23、已知△ABC的三边长为有理数 （1） 求证cosA是有理数 （2） 对任意正整数n，求证cosnA也是有理数 解析 点评 本题题目构思巧妙，立足知识交汇，巧妙地考查了有理数的性质、余弦定理、两角和与差的三角函数、数学归纳法等数学基础知识。对考生知识综合运用能力、数学思维能力要求较高。‎