- 915.50 KB
- 2021-05-13 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
第一章立体几何
第二章点线面位置关系
一、考点分析
基本图形
1.棱柱——有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体叫做棱柱。
①★
②四棱柱 底面为平行四边形 平行六面体 侧棱垂直于底面 直平行六面体 底面为矩形
长方体 底面为正方形 正四棱柱 侧棱与底面边长相等 正方体
2. 棱锥
棱锥——有一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥。
★正棱锥——如果有一个棱锥的底面是正多边形,并且顶点在底面的射影是底面的中心,这样的棱锥叫做正棱锥。
3.球
球的性质:
①球心与截面圆心的连线垂直于截面;
★②(其中,球心到截面的距离为d、球的半径为R、截面的半径为r)
★球与多面体的组合体:球与正四面体,球与长方体,球与正方体等的内接与外切.
注:球的有关问题转化为圆的问题解决.
球面积、体积公式:(其中R为球的半径)
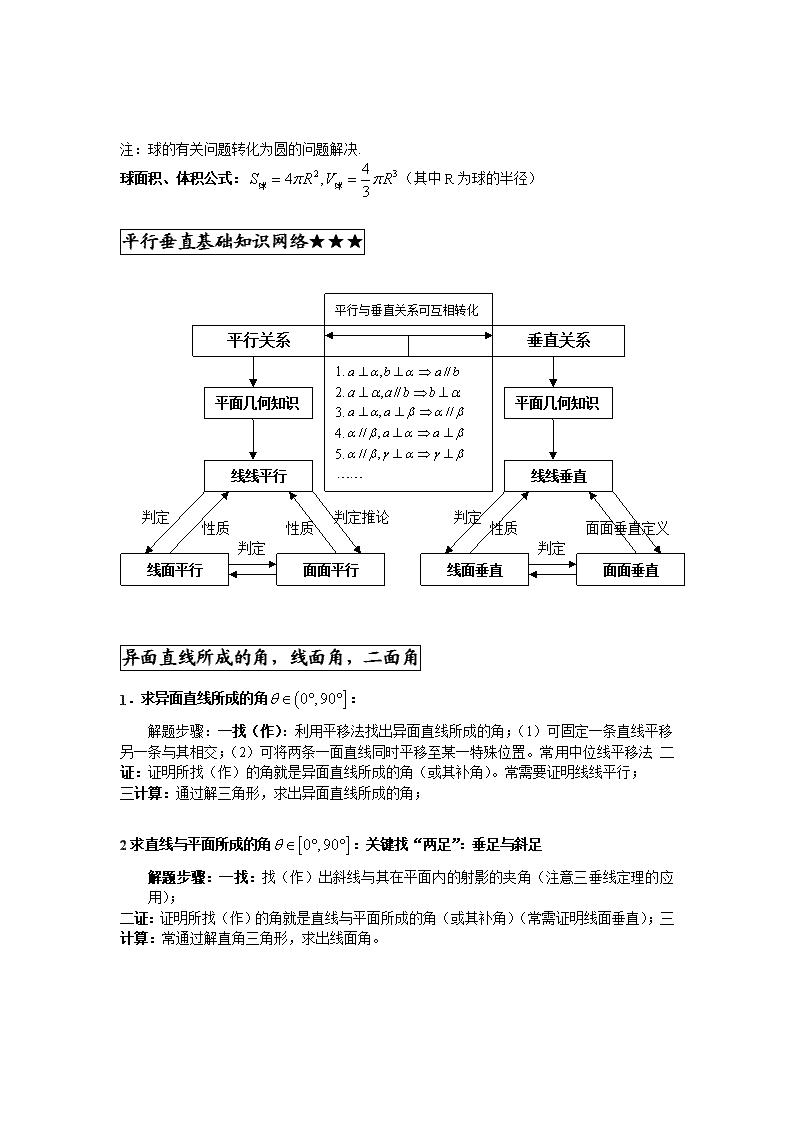
平行垂直基础知识网络★★★
平行关系
平面几何知识
线线平行
线面平行
面面平行
垂直关系
平面几何知识
线线垂直
线面垂直
面面垂直
判定
性质
判定推论
性质
判定
判定
性质
判定
面面垂直定义
1.
2.
3.
4.
5.
平行与垂直关系可互相转化
异面直线所成的角,线面角,二面角
1.求异面直线所成的角:
解题步骤:一找(作):利用平移法找出异面直线所成的角;(1)可固定一条直线平移
另一条与其相交;(2)可将两条一面直线同时平移至某一特殊位置。常用中位线平移法 二证:证明所找(作)的角就是异面直线所成的角(或其补角)。常需要证明线线平行;
三计算:通过解三角形,求出异面直线所成的角;
2求直线与平面所成的角:关键找“两足”:垂足与斜足
解题步骤:一找:找(作)出斜线与其在平面内的射影的夹角(注意三垂线定理的应用);
二证:证明所找(作)的角就是直线与平面所成的角(或其补角)(常需证明线面垂直);三计算:常通过解直角三角形,求出线面角。
注:1体积表面积 异面直线所成角 线面角
1 在正方体的八个顶点中,有四个恰好是正四面体的顶点,则正方体的表面积与此正四面体的表面积的比值为___________.
2.设正六棱锥的底面边长为1,侧棱长为,那么它的体积为_______________.
3.如图7,在正方体中,分别是,中点,求异面直线与所成角的角______________.
4 如图8所示,已知正四棱锥S—ABCD侧棱长为,底面边长为,E是SA的中点,则异面直线BE与SC所成角的大小为_____________.
第8题 第7题
图13
5. 如图9-1-4,在空间四边形中, ,分别是AB、CD的中点,则 与所成角的大小为_____________.
6.如图13在正三棱柱中,,则直线与平面所成角的正弦值为_______________.
7. 一个四面体的所有棱长都为,四个顶点在同一球面上,则此球的表面积为_________.
考点 平行与垂直的证明
1. 正方体,,E为棱的中点.
(Ⅰ) 求证:;
(Ⅱ) 求证:平面;
(Ⅲ)求三棱锥的体积.
2.已知正方体,是底对角线的交点.求证:(1) C1O∥面;(2)面.
3.如图,矩形所在平面,、分别是和的中点.
(Ⅰ)求证:∥平面;
(Ⅱ)求证:;
(Ⅲ)若,求证:平面.
4. 如图(1),ABCD为非直角梯形,点E,F分别为上下底AB,CD上的动点,且。现将梯形AEFD沿EF折起,得到图(2)
(1)若折起后形成的空间图形满足,求证:;
E
B
C
F
D
A
图(2)
(2)若折起后形成的空间图形满足四点共面,求证:平面;
A
B
C
D
E
F
图(1)
A
F
E
B
C
D
M
N
5.如图,在五面体ABCDEF中,FA 平面ABCD,
AD//BC//FE,ABAD,M为EC的中点,
N为AE的中点,AF=AB=BC=FE=AD
(I) 证明平面AMD平面CDE;
(II) 证明平面CDE;
6.在四棱锥P-ABCD中,侧面PCD是正三角形,
且与底面ABCD垂直,已知菱形ABCD中∠ADC=60°,
P
D
A
B
C
O
M
M是PA的中点,O是DC中点.
(1)求证:OM // 平面PCB;
(2)求证:PA⊥CD;
(3)求证:平面PAB⊥平面COM.
7.如图,在四棱锥P—ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
(1)证明PA//平面EDB;(2)证明PB⊥平面EFD
考点异面直线所成的角,线面角 二面角
1.【2008年江苏】16.如图,在四面体中,,点分别是的中点.求证:
(1)直线平面;
(2)平面平面.
2.【2011年】 (18)(本小题满分12分)
如图,已知点P在正方体ABCD-的对角线上,.
(Ⅰ)求DP与所成角的大小;
(Ⅱ)求DP与平面所成角的大小.
3.【2009年山东】 20.(本小题满分12分)
如图,已知四棱锥,底面为菱形,平面,,分别是的中点。
(I)证明:;
(II)若为上的动点,与平面所成最大角的正切值为,求二面角的余弦值。
4.(本小题满分12分)
如图,在三棱锥中,侧面与侧面均为等边三角形,,为中点.
(Ⅰ)证明:平面;
(Ⅱ)求二面角的余弦值.
5【2011年安徽】如图,在四棱锥中,底面是边长为1的菱形,, , ,为的中点,为的中点.
(Ⅰ)证明:直线;
(Ⅱ)求异面直线AB与MD所成角的大小;
(Ⅲ)求点B到平面OCD的距离.
6.【2011年北京】如图,在三棱锥中,,,,.
(Ⅰ)求证:;
(Ⅱ)求二面角的大小;
(Ⅲ)求点到平面的距离.
考点线面、面面关系判断题
1.已知直线l、m、平面α、β,且l⊥α,mβ,给出下列四个命题:
(1)α∥β,则l⊥m (2)若l⊥m,则α∥β
(3)若α⊥β,则l∥m (4)若l∥m,则α⊥β
其中正确的是__________________.
2. 是空间两条不同直线,是空间两条不同平面,下面有四个命题:
① ②
③ ④
其中真命题的编号是________(写出所有真命题的编号)。
3. 为一条直线,为三个互不重合的平面,给出下面三个命题:
①;②;③.
其中正确的命题有_________________.