高考数学按章节分类汇编人教A必修二点直线平面之间的位置关系 40页

‎2012年高考数学按章节分类汇编（人教A必修二）‎ 第二章点直线平面之间的位置关系 一、选择题 ．（2012年高考（浙江文））设是直线,a,β是两个不同的平面 （　　）‎ A．若∥a,∥β,则a∥β B．若∥a,⊥β,则a⊥β ‎ C．若a⊥β,⊥a,则⊥β D．若a⊥β, ∥a,则⊥β ．（2012年高考（四川文））下列命题正确的是 （　　）‎ A．若两条直线和同一个平面所成的角相等,则这两条直线平行 B．若一个平面内有三个点到另一个平面的距离相等,则这两个平面平行 C．若一条直线平行于两个相交平面,则这条直线与这两个平面的交线平行 D．若两个平面都垂直于第三个平面,则这两个平面平行 ．（2012年高考（浙江理））已知矩形ABCD,AB=1,BC=.将ABD沿矩形的对角线BD所在的直线进行翻着,在翻着过程中, （　　）‎ A．存在某个位置,使得直线AC与直线BD垂直 ‎ B．存在某个位置,使得直线AB与直线CD垂直 ‎ C．存在某个位置,使得直线AD与直线BC垂直 ‎ D．对任意位置,三直线“AC与BD”,“AB与CD”,“AD与BC”均不垂直 ．（2012年高考（四川理））下列命题正确的是 （　　）‎ A．若两条直线和同一个平面所成的角相等,则这两条直线平行 B．若一个平面内有三个点到另一个平面的距离相等,则这两个平面平行 C．若一条直线平行于两个相交平面,则这条直线与这两个平面的交线平行 D．若两个平面都垂直于第三个平面,则这两个平面平行 ．（2012年高考（上海春））已知空间三条直线若与异面,且与异面,则 [答] （　　）‎ A．与异面. B．与相交.‎ C．与平行. D．与异面、相交、平行均有可能.‎ 二、填空题 ．（2012年高考（四川文））如图,在正方体中,、分别是、的中点,则异面直线与所成的角的大小是____________.‎ ．（2012年高考（大纲文））已知正方形中,分别为,的中点,那么异面直线与所成角的余弦值为____.‎ ．（ 2012年高考（四川理））如图,在正方体中,、分别是、的中点,则异面直线与所成角的大小是____________.‎ ．（2012年高考（大纲理））三棱柱中,底面边长和侧棱长都相等,,则异面直线与所成角的余弦值为_____________.‎ 三、解答题 ．（2012年高考（重庆文））(本小题满分12分,(Ⅰ)小问4分,(Ⅱ)小问8分)已知直三棱柱中,,,为的中点.(Ⅰ)求异面直线和的距离;(Ⅱ)若,求二面角的平面角的余弦值.‎ ．（2012年高考（浙江文））如图,在侧棱锥垂直底面的四棱锥ABCD-A1B‎1C1D1中,AD∥BC,AD⊥AB,AB=.AD=2,BC=4,AA1=2,E是DD1的中点,F是平面B‎1C1E与直线AA1的交点.‎ (1)证明:(i)EF∥A1D1;‎ ‎(ii)BA1⊥平面B‎1C1EF;‎ ‎(2)求BC1与平面B‎1C1EF所成的角的正弦值.‎ ．（2012年高考（天津文））如图,在四棱锥中,底面是矩形,,.‎ ‎(I)求异面直线与所成角的正切值;‎ ‎(II)证明平面平面;‎ ‎(III)求直线与平面所成角的正弦值.‎ ．（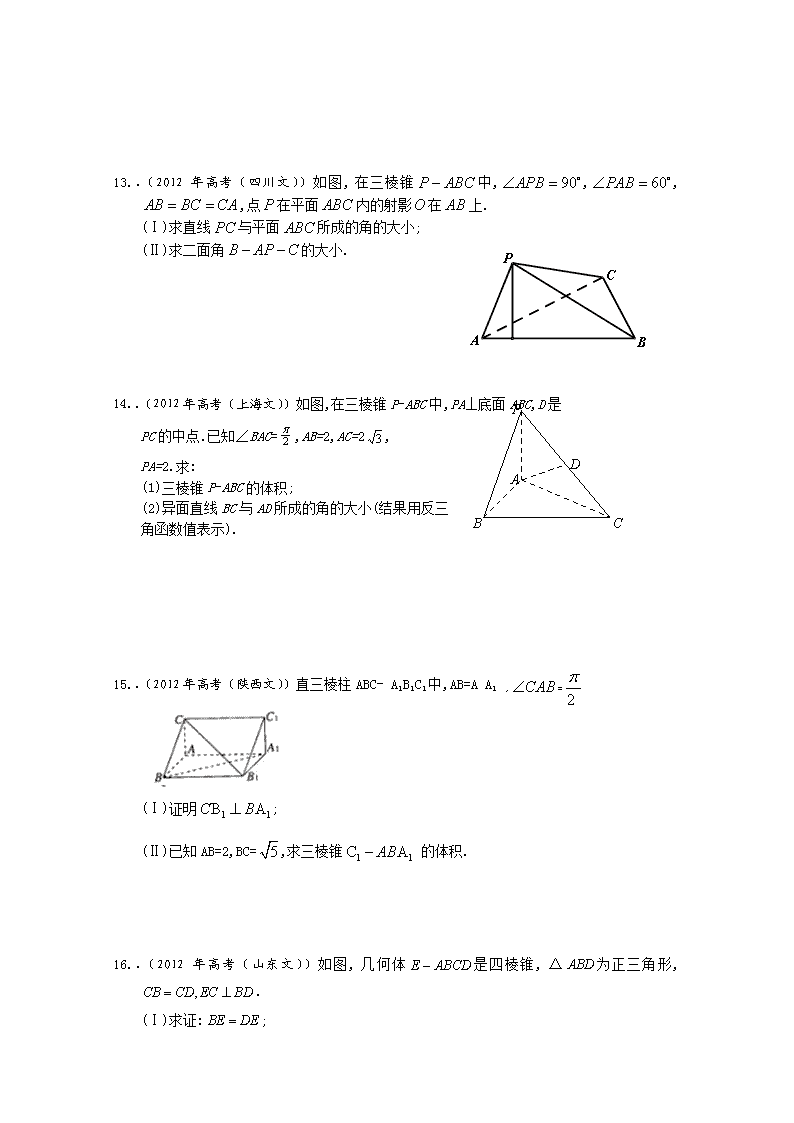2012年高考（四川文））如图,在三棱锥中,,,,点在平面内的射影在上.‎ ‎(Ⅰ)求直线与平面所成的角的大小;‎ ‎(Ⅱ)求二面角的大小.‎ ．（2012年高考（上海文））P A B C D 如图,在三棱锥P-ABC中,PA⊥底面ABC,D是 PC的中点.已知∠BAC=,AB=2,AC=2,‎ PA=2.求:‎ ‎(1)三棱锥P-ABC的体积;‎ ‎(2)异面直线BC与AD所成的角的大小(结果用反三 角函数值表示).‎ ．（2012年高考（陕西文））直三棱柱ABC- A1B‎1C1中,AB=A A1 ,=‎ ‎(Ⅰ)证明;[‎ ‎(Ⅱ)已知AB=2,BC=,求三棱锥 的体积.‎ ．（2012年高考（山东文））如图,几何体是四棱锥,△为正三角形,.‎ ‎(Ⅰ)求证:;‎ ‎(Ⅱ)若∠,M为线段AE的中点,‎ 求证:∥平面.‎ ．（2012年高考（辽宁文））如图,直三棱柱,,‎ AA′=1,点M,N分别为和的中点.‎ ‎(Ⅰ)证明:∥平面;‎ ‎(Ⅱ)求三棱锥的体积.‎ ‎(椎体体积公式V=Sh,其中S为地面面积,h为高)‎ ．（2012年高考（课标文））如图,三棱柱中,侧棱垂直底面,∠ACB=90°,AC=BC=AA1,D是棱AA1的中点.‎ ‎(I) 证明:平面⊥平面 ‎(Ⅱ)平面分此棱柱为两部分,求这两部分体积的比.‎ ．（2012年高考（江西文））如图,在梯形ABCD中,AB∥CD,E,F是线段AB上的两点,且DE⊥AB,CF⊥AB,AB=12,AD=5,BC=4,DE=4.现将△ADE,△‎ CFB分别沿DE,CF折起,使A,B两点重合与点G,得到多面体CDEFG.‎ ‎(1) 求证:平面DEG⊥平面CFG;‎ ‎(2) 求多面体CDEFG的体积.‎ ．（2012年高考（湖南文））如图6,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是等腰梯形,AD∥BC,AC⊥BD.‎ ‎(Ⅰ)证明:BD⊥PC;‎ ‎(Ⅱ)若AD=4,BC=2,直线PD与平面PAC所成的角为30°,求四棱锥P-ABCD的体积.‎ ．（2012年高考（湖北文））某个实心零部件的形状是如图所示的几何体,其下部是底面均是正方形,侧面是全等的等腰梯形的四棱台,上不是一个底面与四棱台的上底面重合,侧面是全等的矩形的四棱柱.‎ ‎(1) 证明:直线平面;‎ ‎(2) 现需要对该零部件表面进行防腐处理,已知(单位:厘米),每平方厘米的加工处理费为元,需加工处理费多少元?‎ ．（2012年高考（广东文））(立体几何)如图5所示,在四棱锥中,‎ 平面,∥,,是的中点,是上的点且,为中边上的高.‎ ‎(Ⅰ)证明:平面;‎ ‎(Ⅱ)若,,,求三棱锥的体积;‎ ‎(Ⅲ)证明:平面.‎ ．（2012年高考（福建文））如图,在长方体中,为棱上的一点.‎ ‎(1)求三棱锥的体积;‎ ‎(2)当取得最小值时,求证:平面.‎ ．（2012年高考（大纲文））如图,四棱锥中,底面为菱形,底面,,,是上的一点,.‎ ‎(Ⅰ)证明:平面;‎ D A B P C E ‎(Ⅱ)设二面角为90°,求与平面所成角的大小.‎ ．（2012年高考（北京文））如图1,在Rt△ABC中,∠C=90°,D,E分别是AC,AB上的中点,‎ 点F为线段CD上的一点.将△ADE沿DE折起到△A1DE的位置,使A‎1F⊥CD,如图2. ‎ ‎(1)求证:DE∥平面A1CB;‎ ‎(2)求证:A‎1F⊥BE;‎ ‎(3)线段A1B上是否存在点Q,使A‎1C⊥平面DEQ?说明理由. ‎ ．（2012年高考（安徽文））如图,长方体中,底面是正方形,‎ 是的中点,是棱上任意一点.‎ ‎(Ⅰ)证明: ;‎ ‎(Ⅱ)如果=2,=, , 求 的长.‎ ．（2012年高考（天津理））如图,在四棱锥中,丄平面,丄,丄,,,.‎ ‎(Ⅰ)证明丄;‎ ‎(Ⅱ)求二面角的正弦值;‎ ‎(Ⅲ)设E为棱上的点,满足异面直线BE与CD所成的角为,求AE的长.‎ ．（2012年高考（新课标理））如图,直三棱柱中,,是棱的中点,‎ ‎(1)证明:‎ ‎(2)求二面角的大小.‎ ．（2012年高考（浙江理））如图,在四棱锥P—ABCD中,底面是边长为的菱形,且∠BAD=120°,且PA⊥平面ABCD,PA=,M,N分别为PB,PD的中点.‎ ‎(Ⅰ)证明:MN∥平面ABCD;‎ ‎(Ⅱ) 过点A作AQ⊥PC,垂足为点Q,求二面角A—MN—Q的平面角的余弦值.‎ ．（2012年高考（重庆理））(本小题满分12分(Ⅰ)小问4分(Ⅱ)小问8分)‎ 如图,在直三棱柱 中,AB=4,AC=BC=3,D为AB的中点 ‎(Ⅰ)求点C到平面 的距离;‎ ‎(Ⅱ)若,求二面角 的平面角的余弦值.‎ ．（2012年高考（四川理））如图,在三棱锥中,,,,平面平面.‎ ‎(Ⅰ)求直线与平面所成角的大小;‎ ‎(Ⅱ)求二面角的大小.‎ ．（2012年高考（上海理））如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点.已知AB=2,‎ A B C D P E AD=2,PA=2.求:‎ ‎(1)三角形PCD的面积;‎ ‎(2)异面直线BC与AE所成的角的大小.‎ ．（2012年高考（上海春））如图,正四棱柱的底面边长为,高为,为线段的中点.求:‎ ‎(1)三棱锥的体积;‎ ‎(2)异面直线与所成角的大小(结果用反三角函数值 表示)‎ ．（2012年高考（陕西理））(1)如图,证明命题“是平面内的一条直线,是外的一条直线(不垂直于),是直线在上的投影,若,则”为真.‎ ‎(2)写出上述命题的逆命题,并判断其真假 (不需要证明)‎ ．（2012年高考（山东理））在如图所示的几何体中,四边形是等腰梯形,∥,平面.‎ ‎(Ⅰ)求证:平面;‎ ‎(Ⅱ)求二面角的余弦值.‎ ．（2012年高考（辽宁理）） 如图,直三棱柱,,‎ 点M,N分别为和的中点.‎ ‎(Ⅰ)证明:∥平面;‎ ‎(Ⅱ)若二面角为直二面角,求的值.‎ ．（2012年高考（江西理））在三棱柱中,已知,在在底面的投影是线段的中点。‎ ‎(1)证明在侧棱上存在一点,使得平面,并求出的长;‎ ‎(2)求平面与平面夹角的余弦值。‎ ．（2012年高考（江苏））如图,在直三棱柱中,,分别是棱上的点(点 不同于点),且为的中点.‎ 求证:(1)平面平面;‎ ‎(2)直线平面.‎ ．（2012年高考（湖南理）） 如图5,在四棱锥P-ABCD中,PA⊥平面ABCD,AB=4,BC=3,AD=5,∠DAB=∠ABC=90°,E是CD的中点.‎ ‎(Ⅰ)证明:CD⊥平面PAE;‎ ‎(Ⅱ)若直线PB与平面PAE所成的角和PB与平面ABCD所成的角相等,求四棱锥P-ABCD的体积.‎ A B C D P E 图5‎ ．（2012年高考（湖北理））如图1,,,过动点A作,垂足D在线段BC上且异于点B,连接AB,沿将△折起,使(如图2所示). ‎ ‎(Ⅰ)当的长为多少时,三棱锥的体积最大;‎ ‎(Ⅱ)当三棱锥的体积最大时,设点,分别为棱,的中点,试在 棱上确定一点,使得,并求与平面所成角的大小.‎ D A B C A C D B 图2‎ 图1‎ M E ‎.‎ ‎·‎ ．（2012年高考（广东理））如图5所示,在四棱锥中,底面为矩形,平面,点在线段上,平面.‎ ‎(Ⅰ)证明:平面;‎ ‎(Ⅱ)若,,求二面角的正切值.‎ ．（2012年高考（福建理））如图,在长方体中为中点.‎ ‎(Ⅰ)求证:‎ ‎(Ⅱ)在棱上是否存在一点,使得平面?若存在,求的长;若不存在,说明理由.[ ‎ ‎(Ⅲ)若二面角的大小为,求的长.‎ ．（2012年高考（大纲理））(注意:在试题卷上作答无效)如图,四棱锥中,底面为菱形,底面,,是上的一点,.‎ ‎(1)证明:平面;‎ ‎(2)设二面角为,求与平面所成角的大小.‎ ．（2012年高考（北京理））如图1,在Rt△ABC中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,‎ 且DE∥BC,DE=2,将△ADE沿DE折起到△A1DE的位置,使A‎1C⊥CD,如图2. ‎ ‎(1)求证:A‎1C⊥平面BCDE;‎ ‎(2)若M是A1D的中点,求CM与平面A1BE所成角的大小;‎ ‎(3)线段BC上是否存在点P,使平面A1DP与平面A1BE垂直?说明理由. ‎ ．（2012年高考（安徽理））平面图形如图4所示,其中是矩形,,,‎ ‎.现将该平面图形分别沿和折叠,使与所在平面都 与平面垂直,再分别连接,得到如图2所示的空间图形,对此空间图形解答 下列问题..‎ ‎(Ⅰ)证明:; (Ⅱ)求的长;‎ ‎(Ⅲ)求二面角的余弦值.‎ 参考答案 一、选择题 【答案】B ‎ ‎【命题意图】本题考查的是平面几何的基本知识,具体为线面平行、线面垂直、面面平行、面面垂直的判定和性质. ‎ ‎【解析】利用排除法可得选项B是正确的,∵∥a,⊥β,则a⊥β.如选项A:∥a,∥β时, a⊥β或a∥β;选项C:若a⊥β,⊥a,∥β或;选项D:若若a⊥β, ⊥a,∥β或⊥β. ‎ [答案]C ‎ ‎[解析]若两条直线和同一平面所成角相等,这两条直线可能平行,也可能为异面直线,也可能相交,所以A错;一个平面不在同一条直线的三点到另一个平面的距离相等,则这两个平面平行,故B错;若两个平面垂直同一个平面两平面可以平行,也可以垂直;故D错;故选项C正确. ‎ ‎[点评]本题旨在考查立体几何的线、面位置关系及线面的判定和性质,需要熟练掌握课本基础知识的定义、定理及公式. ‎ 【答案】B ‎ ‎【解析】最简单的方法是取一长方形动手按照其要求进行翻着,观察在翻着过程,即可知选项B是正确的. ‎ [答案]C ‎ ‎[解析]若两条直线和同一平面所成角相等,这两条直线可能平行,也可能为异面直线,也可能相交,所以A错;一个平面不在同一条直线的三点到另一个平面的距离相等,则这两个平面平行,故B错;若两个平面垂直同一个平面两平面可以平行,也可以垂直;故D错;故选项C正确. ‎ ‎[点评]本题旨在考查立体几何的线、面位置关系及线面的判定和性质,需要熟练掌握课本基础知识的定义、定理及公式. ‎ D ‎ 二、填空题 [答案]90º ‎ ‎[解析]方法一:连接D‎1M,易得DN⊥A1D1 ,DN⊥D‎1M, ‎ 所以,DN⊥平面A1MD1, ‎ 又A‎1M平面A1MD1,所以,DN⊥A1D1,故夹角为90º ‎ 方法二:以D为原点,分别以DA, DC, DD1为x, y, z轴,建立空间直角坐标系D—xyz.设正方体边长为2,则D(0,0,0),N(0,2,1),M(0,1,0)A1(2,0,2) ‎ 故, ‎ 所以,cos< = 0,故DN⊥D‎1M,所以夹角为90º ‎ ‎[点评]异面直线夹角问题通常可以采用两种途径: 第一,把两条异面直线平移到同一平面中借助三角形处理; 第二,建立空间直角坐标系,利用向量夹角公式解决. ‎ 【解析】正确的是②④⑤ ‎ ②四面体每个面是全等三角形,面积相等 ‎ ③从四面体每个顶点出发的三条棱两两夹角之和等于 ‎ ④连接四面体每组对棱中点构成菱形,线段互垂直平分 ‎ ⑤从四面体每个顶点出发的三条棱的长可作为一个三角形的三边长 ‎ [解析]方法一:连接D‎1M,易得DN⊥A1D1 ,DN⊥D‎1M, ‎ 所以,DN⊥平面A1MD1, ‎ 又A‎1M平面A1MD1,所以,DN⊥A1D1,故夹角为90º ‎ 方法二:以D为原点,分别以DA, DC, DD1为x, y, z轴,建立空间直角坐标系D—xyz.设正方体边长为2,则D(0,0,0),N(0,2,1),M(0,1,0)A1(2,0,2) ‎ 故, ‎ 所以,cos< = 0,故DN⊥D‎1M,所以夹角为90º ‎ 答案 ‎ ‎【命题意图】本试题考查了斜棱柱中异面直线的角的求解.用空间向量进行求解即可. ‎ ‎【解析】设该三棱柱的边长为1,依题意有,则 ‎ 而 ‎ ‎ ‎ ‎ ‎ 三、解答题 【答案】:(Ⅰ)(Ⅱ) ‎ ‎【解析】:(Ⅰ)如答(20)图1,因AC=BC, D为AB的中点,故CD AB.又直三棱柱中, 面 ,故 ,所以异面直线 和AB的距离为 ‎ ‎(Ⅱ):由故 面 ,从而 ,故 为所求的二面角的平面角. ‎ 因是在面上的射影,又已知 由三垂线定理的逆定理得从而,都与互余,因此,所以≌,因此得 ‎ 从而 ‎ 所以在中,由余弦定理得 ‎ 【命题意图】本题主要以四棱锥为载体考查线线平行,线面垂直和线面角的计算,注重与平面几何的综合, 同时考查空间想象能力和推理论证能力. ‎ ‎(1)(i)因为, 平面ADD‎1 A1,所以平面ADD‎1 A1. ‎ 又因为平面平面ADD‎1 A1=,所以.所以. ‎ ‎(ii) 因为,所以, ‎ 又因为,所以, ‎ 在矩形中,F是AA的中点,即.即 ‎ ‎,故. ‎ 所以平面. ‎ ‎(2) 设与交点为H,连结. ‎ 由(1)知,所以是与平面所成的角. 在矩形中,,,得,在直角中,,,得 ‎ ‎,所以BC与平面所成角的正弦值是. ‎ 解:(1)如图,在四棱锥中,因为底面是矩形,所以,且,又因为,故或其补角是异面直线与所成的角. ‎ 在中,,所以异面直线与所成角的正切值为2. ‎ ‎(2)证明:由于底面是矩形,故,又由于,,因此平面,而平面,所以平面平面. ‎ ‎(3)在平面内,过点作交直线于点,连接.由于平面平面,由此得为直线与平面所成的角. ‎ 在中,,可得 ‎ 在中, ‎ 由平面,得平面,因此 ‎ 在中,,在中, ‎ 所以直线与平面所成角的正弦值为. ‎ [解析](1)连接OC. 由已知,所成的角 ‎ 设AB的中点为D,连接PD、CD. ‎ 因为AB=BC=CA,所以CDAB. ‎ 因为等边三角形, ‎ 不妨设PA=2,则OD=1,OP=, AB=4. ‎ 所以CD=2,OC=. ‎ 在Rttan ‎ ‎(2)过D作DE于E,连接CE.‎ 由已知可得,CD平面PAB. ‎ 据三垂线定理可知,CE⊥PA, ‎ 所以,. ‎ 由(1)知,DE= ‎ 在Rt△CDE中,tan ‎ 故 ‎ ‎[点评]本题旨在考查线面位置关系和二面角的基础概念,重点考查思维能力和空间想象能力,进一步深化对二面角的平面角的求解.求解二面角平面角的常规步骤:一找(寻找现成的二面角的平面角)、二作(若没有找到现成的,需要引出辅助线作出二面角的平面角)、三求(有了二面角的平面角后,在三角形中求出该角相应的三角函数值). ‎ P A B C D E [解](1), ‎ 三棱锥P-ABC的体积为 ‎ ‎ ‎ ‎(2)取PB的中点E,连接DE、AE,则 ‎ ED∥BC,所以∠ADE(或其补角)是异面直线 ‎ BC与AD所成的角 ‎ 在三角形ADE中,DE=2,AE=,AD=2, ‎ ‎,所以∠ADE=. ‎ 因此,异面直线BC与AD所成的角的大小是 ‎ ‎ 证明:(I)设中点为O,连接OC,OE,则由知, ‎ 又已知,所以平面OCE. ‎ 所以,即OE是BD的垂直平分线,所以. ‎ ‎(II)取AB中点N,连接,∵M是AE的中点,∴∥, ‎ ‎∵△是等边三角形,∴.由∠BCD=120°知,∠CBD=30°, ‎ 所以∠ABC=60°+30°=90°,即,所以ND∥BC, ‎ 所以平面MND∥平面BEC,又DM平面MND,故DM∥平面BEC. ‎ 另证:延长相交于点,连接EF.因为CB=CD,. ‎ 因为△为正三角形,所以,则, ‎ 所以,又, ‎ 所以D是线段AF的中点,连接DM, ‎ 又由点M是线段AE的中点知, ‎ 而平面BEC, 平面BEC,故DM∥平面BEC. ‎ 【答案与解析】 ‎ ‎(1) 证明:取中点P,连结MP,NP,而M,N分别是A与的中点,所以, ‎ MP∥A,PN∥,所以,MP∥平面AC,PN∥平面AC,又,因此平面MPN∥平面AC,而MN平面MPN,所以,MN∥平面AC, ‎ ‎(Ⅱ)（解法一）连结BN，由题意⊥,面∩面=,‎ ‎∴⊥⊥面NBC， ∵==1, ‎ ‎ ∴.‎ ‎(解法2) ‎ ‎【点评】本题以三棱柱为载体主要考查空间中的线面平行的判定、棱锥体积的计算,考查空间想象能力、推理论证能力、运算求解能力,难度适中.第一小题可以通过线线平行来证明线面平行,也可通过面面平行来证明;第二小题求体积根据条件选择合适的底面是关键,也可以采用割补发来球体积. ‎ 【命题意图】本题主要考查空间线线、线面、面面垂直的判定与性质及几何体的体积计算,考查空间想象能力、逻辑推理能力,是简单题. ‎ ‎【解析】(Ⅰ)由题设知BC⊥,BC⊥AC,,∴面, 又∵面,∴, ‎ 由题设知,∴=,即, ‎ 又∵, ∴⊥面, ∵面, ‎ ‎∴面⊥面; ‎ ‎(Ⅱ)设棱锥的体积为,=1,由题意得,==, ‎ 由三棱柱的体积=1, ‎ ‎∴=1:1, ∴平面分此棱柱为两部分体积之比为1:1. ‎ 法二:(I)证明:设,则, ‎ 因侧棱垂直底面,即,所以, ‎ 又D是棱AA1的中点,所以 ‎ 在中,由勾股定理得: ; ‎ 同理,又, ‎ 所以:, ‎ 即有 ‎ 因平面,所以, ‎ 又,所以 ,所以侧面,而平面, ‎ 所以:;由(1)和(2)得:平面, ‎ 又平面 ,所以平面平面 ‎ ‎(II) 平面BDC1分此棱柱的下半部分可看作底面为直角梯形,高为的一个四棱锥,其体积为:, ‎ 该四棱柱的总体积为, ‎ 所以,平面BDC1分此棱柱的上半部的体积为 ‎ 所以 ,所求两部分体积之比为 ‎ 【解析】(1)由已知可得AE=3,BF=4,则折叠完后EG=3,GF=4,又因为EF=5,所以可得 ‎ 又因为,可得,即所以平面DEG⊥平面CFG. ‎ ‎(2)过G作GO垂直于EF,GO 即为四棱锥G-EFCD的高,所以所求体积为 ‎ 【解析】(Ⅰ)因为 ‎ 又是平面PAC内的两条相较直线,所以BD平面PAC, ‎ 而平面PAC,所以. ‎ ‎(Ⅱ)设AC和BD相交于点O,连接PO,由(Ⅰ)知,BD平面PAC, ‎ 所以是直线PD和平面PAC所成的角,从而. ‎ 由BD平面PAC,平面PAC,知. ‎ 在中,由,得PD=2OD. ‎ 因为四边形ABCD为等腰梯形,,所以均为等腰直角三角形, ‎ 从而梯形ABCD的高为于是梯形ABCD面积 ‎ ‎ ‎ 在等腰三角形AOD中, ‎ 所以 ‎ 故四棱锥的体积为. ‎ ‎ ‎ ‎【点评】本题考查空间直线垂直关系的证明,考查空间角的应用,及几何体体积计算.第一问只要证明BD平面PAC即可,第二问由(Ⅰ)知,BD平面PAC,所以是直线PD和平面PAC所成的角,然后算出梯形的面积和棱锥的高,由算得体积. ‎ 【解析】(1)因为四棱柱的侧面是全等的矩形,所以 ‎ 又因为,所以平面 ‎ 连接,因为平面,所以 ‎ 因为底面是正方形,所以.根据棱台的定义可知,与共面. ‎ 又已知平面平面,且平面平面 ‎ 平面,所以,于是 ‎ 由,可得, ‎ 又因为,所以平面. ‎ ‎(2)因为四棱柱的底面是正方形,侧面是全等的矩形,所以 ‎ ‎ ‎ 又因为四棱台的上、下底面均是正方形,侧面是全等的等腰梯形,所以 ‎ ‎ ‎ 于是该实心零部件的表面积为,故所需加工处理费为(元) ‎ ‎【点评】本题考查线面垂直,空间几何体的表面积;考查空间想象,运算求解以及转化与划归的能力.线线垂直线面垂直面面垂直是有关垂直的几何问题的常用转化方法;四棱柱与四棱台的表面积都是由简单的四边形的面积而构成,只需求解四边形的各边长即可.来年需注意线线平行,面面平行特别是线面平行,以及体积等的考查. ‎ 解析:(Ⅰ)因为平面,平面,所以.又因为为中边上的高,所以.,平面,平面,所以平面. ‎ ‎(Ⅱ),因为是的中点,平面,所以点到平面的距离等于,即三棱锥的高,于是. ‎ ‎(Ⅲ)取中点,连接、.因为是的中点,所以且∥.而是上的点且,∥,所以且∥.所以四边形是平行四边形,所以∥.而 ‎,所以.又因为平面,平面,所以.而,平面,平面,所以平面,即平面. ‎ 【考点定位】本题主要考察直线与直线、直线与平面的位置关系以及体积等基本知识,考查空间想象能力、推理论证能力、运算求解能力、数形结合思想、化归与转化思想. ‎ ‎【解析】(1)又长方体AD平面.点A到平面的距离AD=1, ‎ ‎∴==×2×1=1 ,∴ ‎ ‎(2)将侧面绕逆时针转动90°展开,与侧面共面.当,M,C共线时, ‎ ‎+MC取得最小值AD=CD=1 ,=2得M为的中点连接M在中,=MC=,=2, ‎ ‎∴=+ , ∴∠=90°,CM⊥, ‎ ‎∵⊥平面,∴⊥CM ∵AM∩MC=C ‎ ‎∴CM⊥平面,同理可证⊥AM ∴⊥平面MAC ‎ 【命题意图】本试题主要是考查了四棱锥中关于线面垂直的证明以及线面角的求解的运用.从题中的线面垂直以及边长和特殊的菱形入手得到相应的垂直关系和长度,并加以证明和求解. ‎ 解:设,以为原点,为轴,为轴建立空间直角坐标系,则设. ‎ ‎(Ⅰ)证明:由得, 所以,,,所以, ‎ ‎.所以,,所以平面; ‎ ‎(Ⅱ) 设平面的法向量为,又,由得,设平面的法向量为,又,由,得 ‎,由于二面角为,所以,解得. ‎ 所以,平面的法向量为,所以与平面所成角的正弦值为,所以与平面所成角为. ‎ ‎【点评】试题从命题的角度来看,整体上题目与我们平时练习的试题和相似,底面也是特殊的菱形,一个侧面垂直于底面的四棱锥问题,那么创新的地方就是点的位置的选择是一般的三等分点,这样的解决对于学生来说就是比较有点难度的,因此最好使用空间直角坐标系解决该问题为好. ‎ 【考点定位】本题第二问是对基本功的考查,对于知识掌握不牢靠的学生可能不能顺利解决.第三问的创新式问法,难度比较大. ‎ 解:(1)因为D,E分别为AC,AB的中点,所以DE∥BC.又因为DE平面A1CB,所以DE∥平面A1CB. ‎ ‎(2)由已知得AC⊥BC且DE∥BC,所以DE⊥AC.所以DE⊥A1D,DE⊥CD.所以DE⊥平面A1DC.而A‎1F 平面A1DC, ‎ 所以DE⊥A‎1F.又因为A‎1F⊥CD,所以A‎1F⊥平面BCDE.所以A‎1F⊥BE ‎ ‎(3)线段A1B上存在点Q,使A‎1C⊥平面DEQ.理由如下:如图, ‎ 分别取A‎1C,A1B的中点P,Q,则PQ∥BC. ‎ 又因为DE∥BC,所以DE∥PQ.所以平面DEQ即为平面DEP. ‎ 由(2)知DE⊥平面A1DC,所以DE⊥A‎1C. ‎ 又因为P是等腰三角形DA‎1C底边A‎1C 的中点, ‎ 所以A‎1C⊥DP,所以A‎1C⊥平面DEP,从而A‎1C⊥平面DEQ. ‎ 故线段A1B上存在点Q,使得A‎1C⊥平面DEQ. ‎ 【解析】(I)连接,共面 ‎ 长方体中,底面是正方形 ‎ 面 ‎ ‎(Ⅱ)在矩形中, ‎ 得: ‎ 【命题意图】本小题主要考查空间两条直线的位置关系,二面角、异面直线所成的角,直线与平面垂直等基础知识,考查用空间向量解决立体几何问题的方法,考查空间想象能力、运算能力和推理论证能力. ‎ 方法一:（1）以为正半轴方向，建立空间直角左边系 则 ‎（2），设平面的法向量 则 取 是平面的法向量 得：二面角的正弦值为 ‎（3）设；则，‎ ‎ 即 方法二: ‎ ‎（1）以为正半轴方向，建立空间直角左边系 ‎ 则 ‎ ‎ ‎（2），设平面的法向量 ‎ 则 取 ‎ 是平面的法向量 ‎ ‎ ‎ 得：二面角的正弦值为 ‎（3）设；则，‎ ‎ 即 ‎【点评】试题从命题的角度来看,整体上题目与我们平时练习的试题相似,但底面是非特殊 ‎ 的四边形,一直线垂直于底面的四棱锥问题,那么创新的地方就是第三问中点E的位置是不确定的,需要学生根据已知条件进行确定,如此说来就有难度,因此最好使用空间直角坐标系解决该问题为好. ‎ 【解析】(1)在中, ‎ 得: ‎ 同理: ‎ 得:面 ‎ ‎(2)面 ‎ 取的中点,过点作于点,连接 ‎ ‎,面面面 ‎ ‎ 得:点与点重合 ‎ 且是二面角的平面角 ‎ 设,则, ‎ 既二面角的大小为 ‎ 【解析】本题主要考察线面平行的证明方法,建系求二面角等知识点. ‎ ‎(Ⅰ)如图连接BD. ‎ ‎∵M,N分别为PB,PD的中点, ‎ ‎∴在PBD中,MN∥BD. ‎ 又MN平面ABCD, ‎ ‎∴MN∥平面ABCD; ‎ ‎(Ⅱ)如图建系: ‎ A(0,0,0),P(0,0,),M(,,0), ‎ N(,0, 0),C(,3,0). ‎ 设Q(x,y,z),则. ‎ ‎∵,∴. ‎ 由,得:. 即:. ‎ 对于平面AMN:设其法向量为. ‎ ‎∵. ‎ 则. ∴. ‎ 同理对于平面AMN得其法向量为. ‎ 记所求二面角A—MN—Q的平面角大小为, ‎ 则. ‎ ‎∴所求二面角A—MN—Q的平面角的余弦值为. ‎ ‎【答案】(Ⅰ)见解析;(Ⅱ) . ‎ 【考点定位】本小题主要考查立体几何的相关知识,具体涉及到线面垂直的关系,二面角的求法及空间向量在立体几何中的应用,解决此类问题的关键是熟悉几何体的结构特征,熟练进行线线垂直与线面垂直的转化,主要考查学生的空间想象能力与推理论证能力.本题可以利用空间向量来解题,从而降低了题目的难度. ‎ 解:(1)由,为的中点,得,又,故,所以点到平面的距离为 ‎ ‎(2)如图,取为的中点,连结,则,又由(1)知,故,所以为所求的二面角的平面角. ‎ 因为在面上的射影,又已知,由三垂线定理的逆定理得,从而都与互余,因此,所以,因此,,即,得. ‎ 从而,所以,在中,‎ ‎ ‎ [解析](1)连接OC.由已知,所成的角 ‎ 设AB的中点为D,连接PD、CD. ‎ 因为AB=BC=CA,所以CDAB. ‎ 因为等边三角形, ‎ 不妨设PA=2,则OD=1,OP=,AB=4. ‎ 所以CD=2,OC=. ‎ 在Rttan. ‎ 故直线PC与平面ABC所成的角的大小为arctan ‎ ‎(2)过D作DE于E,连接CE. ‎ 由已知可得,CD平面PAB ‎ 根据三垂线定理可知,CE⊥PA, ‎ 所以,. ‎ 由(1)知,DE= ‎ 在Rt△CDE中,tan ‎ 故 ‎ ‎[点评]本小题主要考查线面关系、直线与平面所成的角、二面角等基础知识,考查思维能力、空间想象能力,并考查应用向量知识解决数学问题的能力. ‎ A B C D P E x y z [解](1)因为PA⊥底面ABCD,所以PA⊥CD,又AD⊥CD,所以CD⊥平面PAD, ‎ 从而CD⊥PD ‎ 因为PD=,CD=2, ‎ 所以三角形PCD的面积为 ‎ ‎(2)[解法一]如图所示,建立空间直角坐标系, ‎ 则B(2, 0, 0),C(2, 2,0),E(1, , 1), ‎ ‎, ‎ 设与的夹角为q,则 ‎ ‎,q=. ‎ A B C D P E F 由此可知,异面直线BC与AE所成的角的大小是 ‎ ‎[解法二]取PB中点F,连接EF、AF,则 ‎ EF∥BC,从而∠AEF(或其补角)是异面直线 ‎ BC与AE所成的角 ‎ 在中,由EF=、AF=、AE=2 ‎ 知是等腰直角三角形, ‎ 所以∠AEF=. ‎ 因此异面直线BC与AE所成的角的大小是 ‎ 解(1),又为三棱锥的高, ‎ ‎(2),所以或其补角为导面直线与所成的角. ‎ 连接平面,在中, ‎ ‎,故,即异面直线与所成的角为 ‎ 解析:(1)证法一 如图,过直线上任一点作平面的垂线,设直线的方向向量分别是,则共面,根据平面向量基本定理,存在实数使得 ‎ 则 ‎ 因为,所以 ‎ 又因为,,所以 ‎ 故,从而 ‎ 证法二 如图,记,为直线上异于点A的任意一点,过P作 ‎,垂足为O,则 ‎ ‎∵,,∴直线 ‎ 又,平面, ‎ ‎∴平面,又平面,∴ ‎ ‎(2)逆命题:a是平面内一条直线,是外的一条直线(不垂直于),是直线在上的投影,若,则. 逆命题为真命题. ‎ 解析:(Ⅰ)在等腰梯形ABCD中,AB∥CD,∠DAB=60°,CB=CD, ‎ 由余弦定理可知, ‎ 即,在中,∠DAB=60°,,则为直角三角形,且.又AE⊥BD,平面AED,平面AED,且,故BD⊥平面AED; ‎ ‎(Ⅱ)由(Ⅰ)可知,设,则,建立如图所示的空间直角坐标系,,向量为平面的一个法向量. ‎ 设向量为平面的法向量,则,即, ‎ 取,则,则为平面的一个法向量. ‎ ‎,而二面角F-BD-C的平面角为锐角,则 ‎ 二面角F-BD-C的余弦值为. ‎ 解法二:取的中点,连接,由于,因此, ‎ 又平面,平面,所以 ‎ 由于平面,所以平面 ‎ 故,所以为二面角的平面角.在等腰三角形中,由于,因为,又,所以, ‎ 故,因此二面角的余弦值为. ‎ 【答案及解析】 ‎ ‎【命题意图】本题主要考查线面平行的判定、二面角的计算，考查空间想象能力、运算求解能力，是容易题.‎ ‎【解析】（1）连结，由已知 三棱柱为直三棱柱，‎ 所以为中点.又因为为中点 所以，又平面 ‎ 平面，因此 ……6分 ‎（2）以为坐标原点，分别以直线为轴，轴，轴建立直角坐标系，如图所示 设则，‎ 于是，‎ 所以，设是平面的法向量，‎ 由得，可取 设是平面的法向量，‎ 由得，可取 因为为直二面角，所以，解得……12分 ‎【点评】本题以三棱柱为载体主要考查空间中的线面平行的判定,借助空间直角坐标系求平面的法向量的方法,并利用法向量判定平面的垂直关系,考查空间想象能力、推理论证能力、运算求解能力,难度适中.第一小题可以通过线线平行来证明线面平行,也可通过面面平行来证明. ‎ 【解析】 ‎ 解:(1)证明:连接AO,在中,作于点E,因为,得, ‎ B y O C A E z A11‎ B1‎ C1‎ x 因为平面ABC,所以,因为, ‎ 得,所以平面,所以, ‎ 所以平面, ‎ 又, ‎ 得 ‎ ‎(2)如图所示,分别以所在的直线 ‎ 为x,y,z轴建立空间直角坐标系,则A(1,0,0), C(0,-2,0), A1(0.0,2),B(0,2,0) ‎ 由(1)可知得点E的坐标为,由(1)可知平面的法向量是,设平面的法向量, ‎ 由,得,令,得,即 ‎ 所以 ‎ 即平面平面与平面BB‎1C1C夹角的余弦值是. ‎ ‎【点评】本题考查线面垂直,二面角、向量法在解决立体几何问题中的应用以及空间想象的能力. 高考中,立体几何解答题一般有以下三大方向的考查.一、考查与垂直,平行有关的线面关系的证明;二、考查空间几何体的体积与表面积;三、考查异面角,线面角,二面角等角度问题.前两种考查多出现在第1问,第3种考查多出现在第2问;对于角度问题,一般有直接法与空间向量法两种求解方法. ‎ 【答案】证明:(1)∵是直三棱柱,∴平面. ‎ 又∵平面,∴. ‎ 又∵平面,∴平面. ‎ 又∵平面,∴平面平面. ‎ ‎(2)∵,为的中点,∴. ‎ 又∵平面,且平面,∴. ‎ 又∵平面,,∴平面. ‎ 由(1)知,平面,∴∥. ‎ 又∵平面平面,∴直线平面 ‎ ‎【考点】直线与平面、平面与平面的位置关系. ‎ ‎【解析】(1)要证平面平面,只要证平面上的平面即可.它可由已知是直三棱柱和证得. ‎ ‎(2)要证直线平面,只要证∥平面上的即可. ‎ 【解析】 ‎ 解法1(Ⅰ如图(1)),连接AC,由AB=4,, ‎ E是CD的中点,所以 ‎ 所以 ‎ 而内的两条相交直线,所以CD⊥平面PAE. ‎ ‎(Ⅱ)过点B作 ‎ 由(Ⅰ)CD⊥平面PAE知,BG⊥平面PAE.于是为直线PB与平面PAE ‎ 所成的角,且. ‎ 由知,为直线与平面所成的角. ‎ 由题意,知 ‎ 因为所以 ‎ 由所以四边形是平行四边形,故于是 ‎ 在中,所以 ‎ ‎ ‎ 于是 ‎ 又梯形的面积为所以四棱锥的体积为 ‎ ‎ ‎ A B C D P E 图 ②‎ x y z ‎3‎ ‎4‎ ‎5‎ h 解法2:如图(2),以A为坐标原点,所在直线分别为建立空间直角坐标系.设 则相关的各点坐标为: ‎ ‎ ‎ ‎(Ⅰ)易知因为 ‎ 所以而是平面内的两条相交直线,所以 ‎ ‎(Ⅱ)由题设和(Ⅰ)知,分别是,的法向量,而PB与 ‎ 所成的角和PB与所成的角相等,所以 ‎ ‎ ‎ 由(Ⅰ)知,由故 ‎ ‎ ‎ 解得. ‎ 又梯形ABCD的面积为,所以四棱锥的体积为 ‎ ‎. ‎ ‎【点评】本题考查空间线面垂直关系的证明,考查空间角的应用,及几何体体积计算.第一问只要证明即可,第二问算出梯形的面积和棱锥的高,由算得体积,或者建立空间直角坐标系,求得高几体积. ‎ 考点分析:本题考察立体几何线面的基本关系,考察如何取到最值,用均值不等式和导数均可求最值.同时考察直线与平面所成角.本题可用综合法和空间向量法都可以.运用空间向量法对计算的要求要高些. ‎ 解析: ‎ ‎(Ⅰ)解法1:在如图1所示的△中,设,则. ‎ 由,知,△为等腰直角三角形,所以. ‎ 由折起前知,折起后(如图2),,,且, ‎ 所以平面.又,所以.于是 ‎ ‎ ‎ ‎, ‎ 当且仅当,即时,等号成立, ‎ 故当,即时, 三棱锥的体积最大. ‎ 解法2: ‎ 同解法1,得. ‎ 令,由,且,解得. ‎ 当时,;当时,. ‎ 所以当时,取得最大值. ‎ 故当时, 三棱锥的体积最大. ‎ ‎(Ⅱ)解法1:以为原点,建立如图a所示的空间直角坐标系. ‎ 由(Ⅰ)知,当三棱锥的体积最大时,,. ‎ 于是可得,,,,,, ‎ 且. ‎ 设,则. 因为等价于,即 ‎ ‎,故,. ‎ 所以当(即是的靠近点的一个四等分点)时,. ‎ 设平面的一个法向量为,由 及, ‎ 得 可取. ‎ 设与平面所成角的大小为,则由,,可得 ‎ C A D B 图a E M x y z 图b C A D B E F M N ‎ 图c B D P C F N E B G M N E H 图d N ‎ ‎,即. ‎ 故与平面所成角的大小为 ‎ 解法2:由(Ⅰ)知,当三棱锥的体积最大时,,. ‎ 如图b,取的中点,连结,,,则∥. ‎ 由(Ⅰ)知平面,所以平面. ‎ 如图c,延长至P点使得,连,,则四边形为正方形, ‎ 所以. 取的中点,连结,又为的中点,则∥, ‎ 所以. 因为平面,又面,所以. ‎ 又,所以面. 又面,所以. ‎ 因为当且仅当,而点F是唯一的,所以点是唯一的. ‎ 即当(即是的靠近点的一个四等分点),. ‎ 连接,,由计算得, ‎ 所以△与△是两个共底边的全等的等腰三角形, ‎ 如图d所示,取的中点,连接,, ‎ 则平面.在平面中,过点作于, ‎ 则平面.故是与平面所成的角. ‎ 在△中,易得,所以△是正三角形, ‎ 故,即与平面所成角的大小为 ‎ 解析:(Ⅰ)因为平面,平面,所以.又因为平面,平面,所以.而,平面,平面,所以平面. ‎ ‎(Ⅱ)由(Ⅰ)可知平面,而平面,所以,而为矩形,所以为正方形,于是. ‎ 法1:以点为原点,、、为轴、轴、轴,建立空间直角坐标系.则、、、,于是,.设平面的一个法向量为,则,从而,令,得.而平面的一个法向量为.所以二面角的余弦值为,于是二面角的正切值为3. ‎ 法2:设与交于点,连接.因为平面,平面,平面,所以,,于是就是二面角的平面角.又因为平面,平面,所以是直角三角形.由∽可得 ‎,而,所以,,而,所以,于是,而,于是二面角的正切值为. ‎ 【考点定位】本题考查直线与直线、直线与平面以及二面角等基础知识、考查空间想象能力、推理论证能力、运算求解能力,考查函数与方程思想、数形结合思想、转化与化归的思想. ‎ 解:(1)以点A为原点建立空间直角坐标系,设,则 ‎ ‎ ‎ ‎ ‎ ‎,故 ‎ ‎(2)假设在棱上存在一点,使得平面,则 ‎ 设平面的法向量为,则有,取,可得,要使平面,只要 ‎ ‎,又平面,存在点使平面,此时. ‎ ‎(3)连接,由长方体,得 ‎ ‎,,由(1)知,故平面. ‎ 是平面的法向量,而,则 ‎ ‎ ‎ 二面角是,所以,即 ‎ 【命题意图】本试题主要是考查了四棱锥中关于线面垂直的证明以及线面角的求解的运用. ‎ 从题中的线面垂直以及边长和特殊的菱形入手得到相应的垂直关系和长度,并加以证明和求解. ‎ 解:设,以为原点,为轴,为轴建立空间直角坐标系,则设. ‎ ‎(Ⅰ)证明:由得, 所以,,,所以, ‎ ‎.所以,,所以平面; ‎ ‎(Ⅱ) 设平面的法向量为,又,由得,设平面的法向量为,又,由,得,由于二面角为,所以,解得. ‎ 所以,平面的法向量为,所以与平面所成角的正弦值为,所以与平面所成角为. ‎ ‎【点评】试题从命题的角度来看,整体上题目与我们平时练习的试题和相似,底面也是特殊的菱形,一个侧面垂直于底面的四棱锥问题,那么创新的地方就是点的位置的选择是一般的三等分点,这样的解决对于学生来说就是比较有点难度的,因此最好使用空间直角坐标系解决该问题为好. ‎ 【考点定位】此题第二问是对基本功的考查,对于知识掌握不牢靠的学生可能不能顺利解答.第三问的创新式问法,难度非常大. ‎ 解:(1), ‎ 平面, ‎ 又平面, ‎ ‎ ‎ 又, ‎ 平面 ‎ ‎(2)如图建系,则,,, ‎ ‎∴, ‎ 设平面法向量为,则∴∴ ‎ ‎∴又∵∴ ‎ ‎∴∴与平面所成角的大小 ‎ ‎(3)设线段上存在点,设点坐标为,则则, ‎ 设平面法向量为,则∴∴ ‎ 假设平面与平面垂直,则,∴,, ‎ ‎∵ ∴不存在线段上存在点,使平面与平面垂直 ‎ 【解析】(I)取的中点为点,连接 ‎ 则,面面面 ‎ 同理:面 得:共面 ‎ 又面 ‎ ‎(Ⅱ)延长到,使 得: ‎ ‎,面面面面 ‎ ‎ ‎ ‎(Ⅲ)是二面角的平面角 ‎ 在中, ‎ 在中, ‎ 得:二面角的余弦值为. ‎