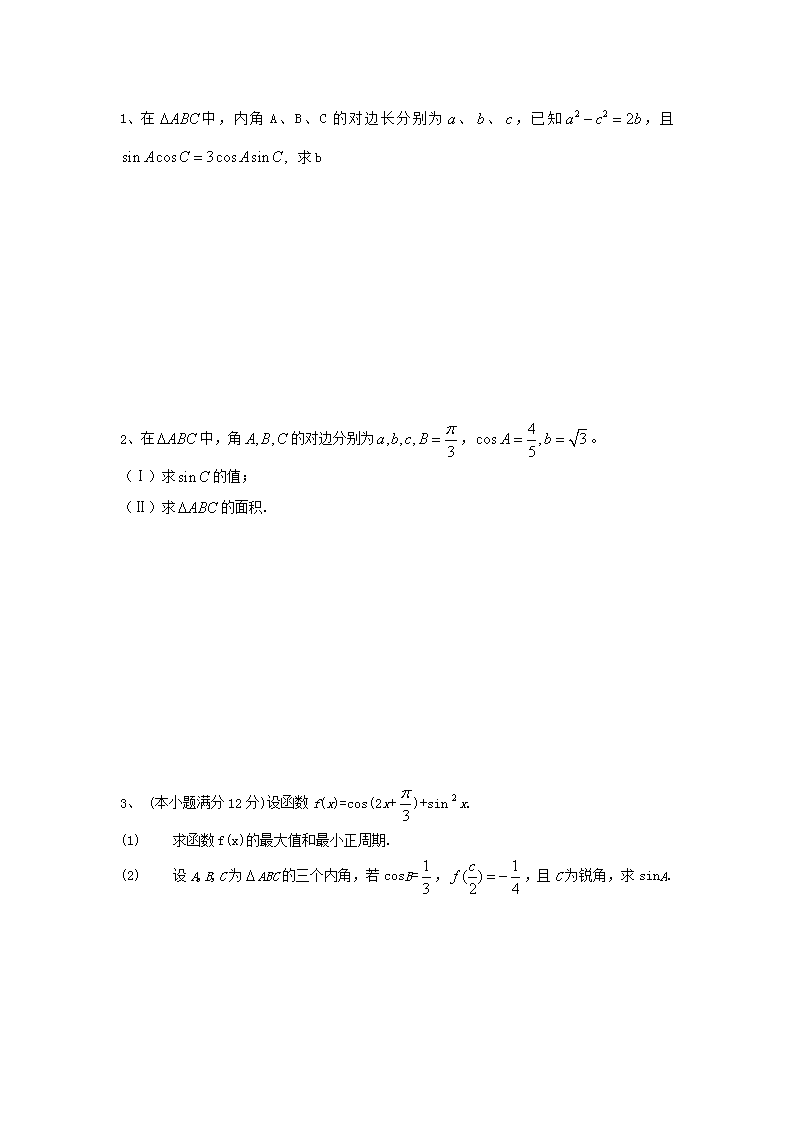三角函数高考题 25页

1、 在中，内角A、B、C的对边长分别为、、，已知，且 求b ‎2、在中，角的对边分别为，。‎ ‎（Ⅰ）求的值；‎ ‎（Ⅱ）求的面积.‎ ‎3、 (本小题满分12分)设函数f(x)=cos(2x+)+sinx.‎ (1) 求函数f(x)的最大值和最小正周期.‎ (2) 设A,B,C为ABC的三个内角，若cosB=，，且C为锐角，求sinA.‎ ‎4、设向量 ‎ ‎（1）若与垂直，求的值； ‎ ‎（2）求的最大值; ‎ ‎（3）若，求证：∥‎ ‎5、在中，角所对应的边分别为，，‎ ‎，求及 ‎6、（本小题满分12分）设△ABC的内角A、B、C的对边长分别为a、b、c，,，求B.‎ ‎7、在△中，所对的边分别为，，．‎ ‎（1）求；‎ ‎（2）若，求,，．‎ ‎8、△中，所对的边分别为，,.‎ ‎（1）求；‎ ‎（2）若,求. ‎ ‎9、在锐角△ABC中，a、b、c分别为角A、B、C所对的边，且 ‎(Ⅰ)确定角C的大小： ‎ ‎（Ⅱ）若c＝,且△ABC的面积为,求a＋b的值。‎ ‎10.在，已知，求角A，B，C的大小.‎ ‎11、已知函数（其中）的图象与x轴的交点中，相邻两个交点之间的距离为，且图象上一个最低点为.‎ ‎(Ⅰ)求的解析式；（Ⅱ）当，求的值域.‎ ‎12、已知函数f(x)＝为偶函数，且函数y＝f(x)图象的两相邻对称轴间的距离为 ‎（Ⅰ）求f（）的值；‎ ‎（Ⅱ）将函数y＝f(x)的图象向右平移个单位后，再将得到的图象上各点的横坐标伸长到原来的4倍，纵坐标不变，得到函数y＝g(x)的图象，求g(x)的单调递减区间.‎ ‎13、已知函数，的最大值是1，其图像经过点．‎ ‎（1）求的解析式；‎ ‎（2）已知，且，，求的值．‎ ‎14、已知函数，．‎ ‎（I）设是函数图象的一条对称轴，求的值．‎ ‎（II）求函数的单调递增区间．‎ ‎15、如图，函数的图象与轴交于点，且在该点处切线的斜率为．‎ ‎（1）求和的值；（2）已知点，点是该函数图象上一点，点是的中点，当，时，求的值．‎ ‎16、已知, f(x)=。‎ ‎(1)求函数在[0,p]上的单调增区间；‎ ‎(2)当时，f(x)的最大值为4，求实数m的值。‎ ‎17、已知函数 ‎ ‎ ‎ （1）求 ‎ （2）当的值域。‎ ‎18、已知函数为常数）．‎ ‎（1）求函数的最小正周期；（2）求函数的单调递增区间；‎ ‎(3) 若时，的最小值为，求的值．‎ ‎19、已知函数 ‎（1）将写成的形式，并求其图象对称中心的横坐标；‎ ‎（2）如果△ABC的三边a、b、c满足b2=ac，且边b所对的角为，试求角的范围及此时函数的值域.‎ ‎20、已知函数 ‎ ‎ ‎ （1）求 ‎ （2）当的值域。‎ ‎21、已知 ‎（Ⅰ）求的值；‎ ‎（Ⅱ）求的值。‎ ‎22、已知 ‎（Ⅰ）求的值；（Ⅱ）求的值。‎ ‎23、已知求的值 24、 求函数的最大值与最小值。‎ ‎25、已知<<<,‎ ‎(Ⅰ)求的值. （Ⅱ）求.‎ ‎26、为了测量两山顶M，N间的距离，飞机沿水平方向在A，B两点进行测量，A，B，M，N在同一个铅垂平面内（如示意图），飞机能够测量的数据有俯角和A，B间的距离，请设计一个方案，包括：①指出需要测量的数据（用字母表示，并在图中标出）；②用文字和公式写出计算M，N间的距离的步骤。‎ 27、 如图，A,B,C,D都在同一个与水平面垂直的平面内，B，D为两岛上的两座灯塔的塔顶。测量船于水面A处测得B点和D点的仰角分别为，，于水面C处测得B点和D点的仰角均为，AC=0.1km。试探究图中B，D间距离与另外哪两点间距离相等，然后求B，D的距离（计算结果精确到0.01km，1.414，2.449）‎ ‎29、（如图，测量河对岸的塔高时，可以选与塔底在同一水平面内的两个测点与．现测得，并在点测得塔顶的仰角为，求塔高．‎ 北 乙 甲 ‎30、（山东理20）如图，甲船以每小时海里的速度向正北方航行，乙船按固定方向匀速直线航行，当甲船位于处时，乙船位于甲船的北偏西方向的处，此时两船相距海里，当甲船航行分钟到达处时，乙船航行到甲船的北偏西方向的处，此时两船相距海里，问乙船每小时航行多少海里？‎ ‎1、解法一：在中则由正弦定理及余弦定理有:化简并整理得：.又由已知.解得. ‎ 解法二:由余弦定理得: .又,。‎ 所以…………………………………①‎ 又，‎ ‎，即 由正弦定理得，故………………………②‎ 由①，②解得。‎ ‎2、解（Ⅰ）∵A、B、C为△ABC的内角，且，‎ ‎∴，‎ ‎∴.‎ ‎（Ⅱ）由（Ⅰ）知，‎ ‎ 又∵，∴在△ABC中，由正弦定理，‎ ‎∴.‎ ‎∴△ABC的面积 ‎3、解（1）f(x)=cos(2x+)+sinx.=‎ 所以函数f(x)的最大值为,最小正周期. ‎ ‎（2）==－, 所以, 因为C为锐角, 所以,‎ 又因为在ABC 中, cosB=, 所以 , 所以 ‎ ‎.‎ ‎4、‎ ‎5解：由得 ‎∴ ∴‎ ‎∴，又 ‎∴‎ 由得 ‎ 即 ∴‎ 由正弦定理得 ‎6、解：由 cos（AC）+cosB=及B=π（A+C）‎ ‎ cos（AC）cos（A+C）=，‎ cosAcosC+sinAsinC（cosAcosCsinAsinC）=,‎ sinAsinC=.‎ 又由=ac及正弦定理得 ‎ 故，‎ ‎ 或 （舍去），‎ 于是 B= 或 B=.‎ 又由 知或 所以 B=。‎ ‎7、解：（1）由 得 ‎ ‎ 则有 =‎ ‎ 得 即.‎ ‎（2） 由 推出 ；而,‎ 即得,‎ ‎ 则有 解得 ‎ ‎8、解：(1) 因为，即，‎ 所以，‎ 即 ，‎ 得 . 所以,或(不成立).‎ 即 , 得，所以.‎ 又因为，则，或（舍去） ‎ 得 ‎(2)， ‎ 又, 即 ， ‎ 得 ‎9、解（1）由及正弦定理得， ‎ 是锐角三角形，‎ ‎（2）解法1：由面积公式得 由余弦定理得 ‎ 由②变形得 解法2：前同解法1，联立①、②得 消去b并整理得解得 所以故 ‎10、解：设 由得，所以 又因此 ‎ 由得，于是 所以，，因此 ‎，既 由A=知，所以，，从而 或，既或故 或 ‎11、解（1）由最低点为得A=2.‎ 由x轴上相邻的两个交点之间的距离为得=，即，‎ 由点在图像上的 故 ‎ 又 ‎（2）‎ 当=，即时，取得最大值2；当 即时，取得最小值-1，故的值域为[-1,2] ‎ ‎12、解（Ⅰ）f(x)＝‎ ‎＝‎ ‎＝2sin(-)‎ 因为f(x)为偶函数，‎ 所以对x∈R,f(-x)=f(x)恒成立，‎ 因此sin（--）＝sin(-).‎ 即-sincos(-)+cossin(-)=sincos(-)+cossin(-),‎ 整理得 sincos(-)=0.因为＞0，且x∈R,所以cos（-）＝0.‎ 又因为0＜＜π，故　-＝.所以f(x)＝2sin(+)=2cos.‎ 由题意得，所以 故　f(x)=2cos2x.‎ 因为 ‎ ‎（Ⅱ）将f(x)的图象向右平移个个单位后，得到的图象，再将所得图象横坐标伸长到原来的4倍，纵坐标不变，得到的图象.‎ 所以 当 (k∈Z),‎ 即4kπ＋≤≤x≤4kπ+ (k∈Z)时，g(x)单调递减.‎ 因此g(x)的单调递减区间为　　　(k∈Z)‎ ‎13、解（1）依题意有，则，将点代入得，‎ 而，，，故；‎ ‎（2）依题意有，而，‎ ‎，‎ ‎14、解：（I）由题设知．‎ 因为是函数图象的一条对称轴，所以，‎ 即（）．‎ 所以．‎ 当为偶数时，，‎ 当为奇数时，．‎ ‎（II）‎ ‎．‎ 当，即（）时，‎ 函数是增函数，‎ 故函数的单调递增区间是（）．‎ ‎15、解：（1）将，代入函数得，‎ 因为，所以．‎ 又因为，，，所以，‎ 因此．‎ ‎（2）因为点，是的中点，，‎ 所以点的坐标为．‎ 又因为点在的图象上，所以．‎ 因为，所以，‎ 从而得或．‎ 即或．‎ ‎16、解：（1）依题意得：‎ 令 得 ‎ 上的单调增区间为 ‎（2）‎ 依题意得：‎ ‎17、解：（1） ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ （2）‎ ‎ 根据正弦函数的图象可得：‎ ‎ 当时，‎ ‎ 取最大值1 ‎ ‎ 当时 ‎ ‎ ‎ ‎ ‎18、解:(1) ‎ ‎ ‎ ‎∴的最小正周期. ‎ ‎(2) 当, ‎ 即时，函数单调递增，‎ 故所求区间为 ‎ ‎(3) 当时， ‎ ‎∴当时取得最小值, ‎ 即, ∴.‎ ‎19、 ‎ ‎ = ‎ ‎= ‎ 若为其图象对称中心的横坐标，即=0， -‎ ‎， ‎ 解得： ‎ ‎ （2）， ‎ 即，而，所以。 ‎ ‎，， ‎ 所以 ‎ ‎20、解：（1） 2分 ‎ 4分 ‎ ‎ ‎ ‎ ‎ 6分 ‎ （2）‎ ‎ 根据正弦函数的图象可得：‎ ‎ 当时，‎ ‎ 取最大值1 8分 ‎ 当时 ‎ 10分 ‎ ‎ ‎ 即 ‎ ‎21、解：(Ⅰ)由得，即，又，所以为所求。‎ ‎（Ⅱ）=‎ ‎===。‎ ‎22、解：(Ⅰ)由，得，所以＝。‎ ‎（Ⅱ）∵，∴。‎ ‎23、解：‎ ‎24、【解】：‎ ‎ ‎ ‎ ‎ 由于函数在中的最大值为 ‎ 最小值为 故当时取得最大值，当时取得最小值 ‎25、解：（Ⅰ）由，得 ‎∴，于是 ‎（Ⅱ）由 0<<<，得 又∵，∴‎ 由得：‎ 所以 ‎26、 解：方案一：①需要测量的数据有：A ‎ 点到M，N点的俯角；B点到M，‎ N的俯角；A，B的距离 d （如图所示） . ……….3分 ‎ ②第一步：计算AM . 由正弦定理　；‎ ‎ 第二步：计算AN . 由正弦定理　；‎ ‎ 第三步：计算MN. 由余弦定理 .‎ 方案二：①需要测量的数据有：‎ ‎ A点到M，N点的俯角，；B点到M，N点的府角，；A，B的距离 d （如图所示）.‎ ‎ ②第一步：计算BM . 由正弦定理　；‎ ‎　　　第二步：计算BN . 由正弦定理　； ‎ ‎ 第三步：计算MN . 由余弦定理 ‎27、在△ABC中，∠DAC=30°, ∠ADC=60°－∠DAC=30,‎ 所以CD=AC=0.1 又∠BCD=180°－60°－60°=60°，‎ 故CB是△CAD底边AD的中垂线，所以BD=BA，        ……5分 在△ABC中，‎ 即AB=‎ 因此，BD=‎ 故B，D的距离约为0.33km。 ‎ ‎28、解法一（Ⅰ）依题意，有，，又，。‎ 当 是，‎ ‎ 又 ‎（Ⅱ）在△MNP中∠MNP=120°，MP=5，‎ 设∠PMN=，则0°<<60°‎ 由正弦定理得 ‎,‎ 故 ‎0°<<60°，当=30°时，折线段赛道MNP最长 亦即，将∠PMN设计为30°时，折线段道MNP最长 解法二：‎ ‎（Ⅰ）同解法一 ‎（Ⅱ）在△MNP中，∠MNP=120°，MP=5，‎ 由余弦定理得∠MNP=‎ 即 故 从而，即 当且仅当时，折线段道MNP最长 注：本题第（Ⅱ）问答案及其呈现方式均不唯一，除了解法一、解法二给出的两种设计方式，还可以设计为：①；②；③点N在线段MP的垂直平分线上等 ‎29、解：在中，．‎ 由正弦定理得．‎ 所以．‎ 北 甲 乙 在中，．‎ ‎30、解法一：如图，连结，由已知，‎ ‎，‎ ‎，‎ 又，‎ 是等边三角形，‎ ‎，‎ 由已知，，‎ ‎，‎ 在中，由余弦定理，‎ ‎．‎ ‎．‎ 因此，乙船的速度的大小为（海里/小时）．‎ 答：乙船每小时航行海里．‎ 解法二：如图，连结，由已知，，，‎ 北 乙 甲 ‎，‎ ‎．‎ 在中，由余弦定理，‎ ‎．‎ ‎．‎ 由正弦定理 ‎，‎ ‎，即，‎ ‎．‎ 在中，由已知，由余弦定理，‎ ‎．‎ ‎，‎ 乙船的速度的大小为海里/小时．‎ 答：乙船每小时航行海里．‎