高考数学平面解析几何时双曲线更多资料关注微博高中学习资料库 7页

第九章　平面解析几何第8课时　双 曲 线 ‎1. 若双曲线方程为x2－2y2＝1，则它的左焦点的坐标为________．‎ 答案： 解析：∵ 双曲线方程可化为x2－＝1，∴ a2＝1，b2＝.∴ c2＝a2＋b2＝，c＝.∴ 左焦点坐标为.‎ ‎2. 双曲线－＝1的渐近线方程为________．‎ 答案：y＝±2x 解析：∵ a＝2，b＝4，∴ 双曲线的渐近线方程为y＝±2x.‎ ‎3. 若双曲线－y2＝1的一个焦点为(2，0)，则它的离心率为________．‎ 答案： 解析：依题意得a2＋1＝4，a2＝3，故e＝＝＝.‎ ‎4. (选修11P39习题2(2)改编)双曲线的焦点在 x轴上，虚轴长为12，离心率为，则双曲线的标准方程为______________________. ‎ 答案：－＝1‎ 解析：焦点在x轴上，设所求双曲线的方程为－＝1.由题意，得解得∴ 焦点在x轴上的双曲线方程为－＝1.‎ ‎5. 设F1，F2是双曲线x2－＝1的两个焦点，P是双曲线上的一点，且3PF1＝4PF2，则△PF1F2的面积等于________．‎ 答案：24‎ 解析：由P是双曲线上的一点和3PF1＝4PF2可知，PF1－PF2＝2，解得PF1＝8，PF2＝6.又F1F2＝2c＝10，所以△PF1F2为直角三角形，所以△PF1F2的面积S＝×6×8＝24.‎ ‎1. 双曲线的定义 平面内到两个定点F1，F2的距离的差的绝对值等于常数(小于F1F2的正数)的点的轨迹叫做双曲线，这两个定点叫做双曲线的焦点，两焦点间的距离叫做双曲线的焦距．‎ ‎2. 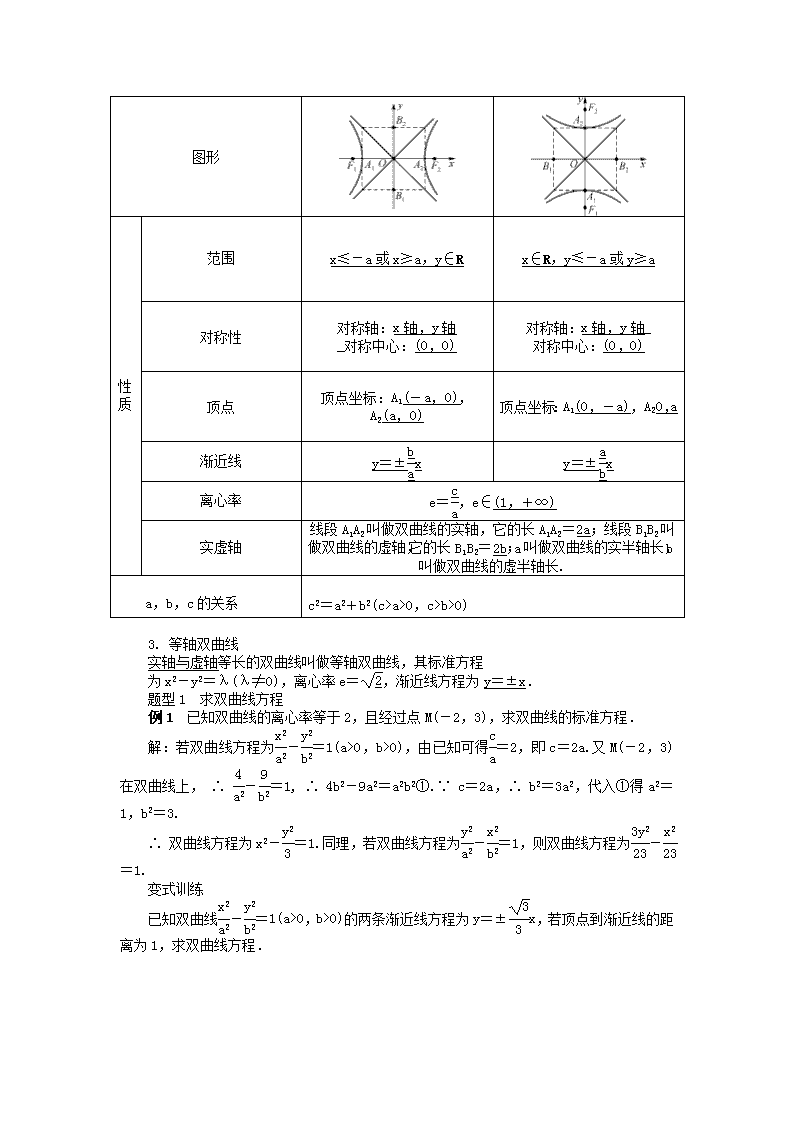双曲线的标准方程和几何性质 标准方程 －＝1(a>0，b>0)‎ －＝1(a>0，b>0)‎ 图形 性质 范围 x≤－a或x≥a，y∈R x∈R，y≤－a或y≥a 对称性 对称轴：x轴，y轴 ‎_对称中心：(0，0)‎ 对称轴：x轴，y轴_‎ 对称中心：(0，0)‎ 顶点 顶点坐标：A1(－a，0)，A2(a，0)‎ 顶点坐标：A1(0，－a)，A20，a 渐近线 y＝±x y＝±x 离心率 e＝，e∈(1，＋∞)‎ 实虚轴 线段A1A2叫做双曲线的实轴，它的长A1A2＝2a；线段B1B2叫做双曲线的虚轴，它的长B1B2＝2b；a叫做双曲线的实半轴长，b叫做双曲线的虚半轴长.‎ a，b，c的关系 c2＝a2＋b2(c>a>0，c>b>0)‎ ‎3. 等轴双曲线 实轴与虚轴等长的双曲线叫做等轴双曲线，其标准方程 为x2－y2＝λ(λ≠0)，离心率e＝，渐近线方程为y＝±x．‎ 题型1　求双曲线方程 ‎ 例1　已知双曲线的离心率等于2，且经过点M(－2，3)，求双曲线的标准方程．‎ 解：若双曲线方程为－＝1(a>0，b>0)，由已知可得＝2，即c＝2a.又M(－2，3)在双曲线上， ∴ －＝1, ∴ 4b2－9a2＝a2b2①.∵ c＝2a，∴ b2＝3a2，代入①得a2＝1，b2＝3.‎ ‎∴ 双曲线方程为x2－＝1.同理，若双曲线方程为－＝1，则双曲线方程为－＝1.‎ 已知双曲线－＝1(a>0，b>0)的两条渐近线方程为y＝±x，若顶点到渐近线的距离为1，求双曲线方程．‎ 解：由题意知：右顶点坐标为(a，0)，其到渐近线的距离为d＝＝＝1，‎ 故a＝2.又渐近线方程为y＝±x，所以b＝，所以双曲线方程为－＝1.‎ 题型2　求双曲线的基本量 例2　已知双曲线的焦点在x轴上，两个顶点间的距离为2，焦点到渐近线的距离为.‎ ‎(1) 求双曲线的标准方程；‎ ‎(2) 写出双曲线的实轴长、虚轴长、焦点坐标、离心率、渐近线方程．‎ 解：(1) 依题意可设双曲线的方程为－＝1(a>0, b>0)，则2a＝2, 所以a＝1.设双曲线的一个焦点为(c, 0), 一条渐近线的方程为bx－ ay ＝ 0，则焦点到渐近线的距离d＝＝b＝，所以双曲线的方程为x2－＝1.‎ ‎(2) 双曲线的实轴长为2，虚轴长为2，焦点坐标为(－， 0), (， 0)，离心率为，渐近线方程为y＝±x.‎ 如图，F1、F2分别是双曲线C：－＝1(a，b＞0)的左、右焦点，B是虚轴的端点，直线F1B与C的两条渐近线分别交于P、Q两点，线段PQ的垂直平分线与x轴交于点M.若MF2＝F1F2，则C的离心率是________．‎ 答案： 解析：设双曲线的焦点坐标为F1(－c，0)，F2(c，0)．‎ ‎∵ B(0，b)，∴ F1B所在的直线为－＋＝1.①‎ 双曲线渐近线为y＝±x，由得Q.‎ 由得P，∴ PQ的中点坐标为.‎ 由a2＋b2＝c2得，PQ的中点坐标可化为.‎ 直线F1B的斜率为k＝，∴ PQ的垂直平分线为y－＝－.‎ 令y＝0，得x＝＋c，∴ M，∴ F2M＝.‎ 由MF2＝F1F2得＝＝2c，即3a2＝2c2，∴ e2＝，∴ e＝.‎ 题型3　与椭圆、抛物线有关的基本量 例3　已知双曲线过点(3，－2)，且与椭圆4x2＋9y2＝36有相同的焦点．‎ ‎(1) 求双曲线的标准方程；‎ ‎(2) 求以双曲线的右准线为准线的抛物线的标准方程．‎ 解：(1) 由题意，椭圆4x2＋9y2＝36的焦点为(±，0)，即c＝，‎ ‎∴ 设所求双曲线的方程为－＝1，‎ ‎∵ 双曲线过点(3，－2)，‎ ‎∴ －＝1, ∴ a2＝3或a2＝15(舍去)．‎ 故所求双曲线的方程为－＝1.‎ ‎(2) 由(1)可知双曲线的右准线为 x＝. ‎ 设所求抛物线的标准方程为y2＝－2px(p>0)，则p＝，故所求抛物线的标准方程为y2＝－x. ‎ 双曲线C与椭圆＋＝1有相同的焦点，直线y＝x为C的一条渐近线．求双曲线C的方程．‎ 解：设双曲线的方程为－＝1(a>0，b>0)，‎ 由椭圆方程＋＝1，求得两焦点为(－2，0)、(2，0)，‎ ‎∴对于双曲线C：c＝2.‎ 又y＝x为双曲线C的一条渐近线，‎ ‎∴＝，解得 a2＝1，b2＝3.‎ ‎∴双曲线C的方程为x2－＝1.‎ ‎1. 已知双曲线C：－＝1的焦距为10，P(2，1)在C的渐近线上，则C的方程为________．‎ 答案：－＝1‎ 解析：∵ －＝1的焦距为10，∴ c＝5＝.①‎ 又双曲线渐近线方程为y＝±x，且P(2，1)在渐近线上，∴ ＝1，即a＝2b.②‎ 由①②解得a＝2，b＝.‎ ‎2. 若双曲线－＝1的离心率e＝2，则m＝________．‎ 答案：48‎ 解析：根据双曲线方程－＝1知a2＝16，b2＝m，并在双曲线中有a2＋b2＝c2，∴ 离心率e＝＝2＝4＝m＝48.‎ ‎3. 已知双曲线x2－y2＝1，点F1，F2为其两个焦点，点P为双曲线上一点，若PF1⊥PF2，则PF1＋PF2＝________．‎ 答案：2 解析：不妨设点P在双曲线的右支上，‎ 因为PF1⊥PF2，所以(2)2＝PF＋PF，‎ 又因为PF1－PF2＝2，‎ 所以(PF1－PF2)2＝4，‎ 可得2PF1·PF2＝4，‎ 则(PF1＋PF2)2＝PF＋PF＋2PF1·PF2＝12，‎ 所以PF1＋PF2＝2.‎ ‎4. 已知双曲线－＝1的右焦点为(3，0)，则该双曲线的离心率为________．‎ 答案： 解析：由题意知c＝3，故a2＋5＝9，解得a＝2，故该双曲线的离心率e＝＝.‎ ‎5. 已知双曲线－＝1(a＞0，b＞0)与抛物线y2＝8x有一个公共的焦点F，且两曲线的一个交点为P，若PF＝5，则双曲线的渐近线方程为________．‎ 答案：y＝±x 解析：设点P(m，n)，依题意得，点F(2，0)，由点P在抛物线y2＝8x上，且PF＝5得由此解得m＝3，n2＝24.于是有由此解得a2＝1，b2＝3，该双曲线的渐近线方程为y＝±x＝±x.‎ ‎6. 已知椭圆＋＝1(a＞b＞c＞0，a2＝b2＋c2)的左、右焦点分别为F1，F2，若以F2为圆心，b－c为半径作圆F2，过椭圆上一点P作此圆的切线，切点为T，且PT的最小值为(a－c)，则椭圆的离心率e的取值范围是________．‎ 答案： 解析：因为PT＝(b＞c)，而PF2的最小值为a－c，所以PT的最小值为.‎ 依题意有，≥(a－c)，‎ 所以(a－c)2≥4(b－c)2，‎ 所以a－c≥2(b－c)，‎ 所以a＋c≥2b，‎ 所以(a＋c)2≥4(a2－c2)，‎ 所以5c2＋2ac－3a2≥0，‎ 所以5e2＋2e－3≥0　①.‎ 又b＞0，所以b2＞c2，所以a2－c2＞c2，‎ 所以2e2＜1　②，‎ 联立①②，得≤e＜.‎ ‎1. 双曲线－＝1上一点P到右焦点的距离是实轴两端点到右焦点距离的等差中项，则P点到左焦点的距离为________．‎ 答案：13‎ 解析：由a＝4，b＝3，得c＝5.设左焦点为F1，右焦点为F2，‎ 则|PF2|＝(a＋c＋c－a)＝c＝5，‎ 由双曲线的定义，得|PF1|＝2a＋|PF2|＝8＋5＝13.‎ ‎2. 已知△ABC外接圆半径R＝，且∠ABC＝120°，BC＝10，边BC在x轴上且y轴垂直平分BC边，则过点A且以B、C为焦点的双曲线方程为______________．‎ 答案：－＝1‎ 解析：∵ sin∠BAC＝＝，∴ cos∠BAC＝，AC＝2Rsin∠ABC＝2××＝14，‎ sin∠ACB＝sin(60°－∠BAC)＝sin 60°cos∠BAC－cos60°·sin∠BAC＝×－×＝，‎ ‎∴ AB＝2Rsin∠ACB＝2××＝6, ‎ ‎∴ 2a＝|AC－AB|＝14－6＝8，‎ ‎∴ a＝4，又c＝5，∴ b2＝c2－a2＝25－16＝9，∴ 所求双曲线方程为－＝1.‎ ‎3. 根据下列条件，求双曲线方程．‎ ‎(1) 与双曲线－＝1有共同的渐近线，且过点(－3，2)；‎ ‎(2) 与双曲线－＝1有公共焦点，且过点(3，2)．‎ 解：解法1：(1) 设双曲线的方程为－＝1，‎ 由题意，得解得a2＝，b2＝4.‎ 所以双曲线的方程为－＝1.‎ ‎(2) 设双曲线方程为－＝1.由题意易求得c＝2.‎ 又双曲线过点(3，2)，∴－＝1.‎ 又∵a2＋b2＝(2) 2，∴a2＝12，b2＝8.‎ 故所求双曲线的方程为－＝1.‎ 解法2：(1) 设所求双曲线方程为－＝λ(λ≠0)，‎ 将点(－3，2)代入得λ＝，所以双曲线方程为－＝.‎ ‎(2) 设双曲线方程为－＝1，‎ 将点(3，2)代入得k＝4，所以双曲线方程为－＝1.‎ ‎4. 已知双曲线－＝1的离心率为2，焦点到渐近线的距离等于，过右焦点F2的直线l交双曲线于A、B两点，F1为左焦点．‎ ‎(1) 求双曲线的方程；‎ ‎(2) 若△F1AB的面积等于6，求直线l的方程．‎ 解：(1) 依题意，b＝，＝2a＝1，c＝2，∴ 双曲线的方程为：x2－＝1.‎ ‎(2) 设A(x1，y1)，B(x2，y2)，F2(2，0)，直线l：y＝k(x－2)，‎ 由消元得(k2－3)x2－4k2x＋4k2＋3＝0，‎ k≠±时，x1＋x2＝，x1x2＝，y1－y2＝k(x1－x2)，‎ ‎△F1AB的面积S＝·＝2|k|·|x1－x2|＝2|k|·＝12|k|·＝6k4＋8k2－9＝0k2＝1k＝±1，‎ 所以直线l的方程为y＝±(x－2)．‎ ‎1. 应用双曲线的定义需注意的问题 在双曲线的定义中要注意双曲线上的点(动点)具备的几何条件，即“到两定点(焦点)的距离之差的绝对值为一常数，且该常数必须小于两定点的距离”．若定义中的“绝对值”去掉，点的轨迹是双曲线的一支．‎ ‎2. 区分双曲线与椭圆中a，b，c的关系，在椭圆中a2＝b2＋c2，而在双曲线中c2＝a2＋b2.双曲线的离心率e＞1，椭圆的离心率e∈(0，1)．‎ ‎3. 双曲线方程的求法 ‎(1) 若不能明确焦点在哪条坐标轴上，设双曲线方程为mx2＋ny2＝1(mn<0)；‎ ‎(2) 与双曲线－＝1有共同渐近线的双曲线方程可设为－＝λ(λ≠0)；‎ ‎(3) 若已知渐近线方程为mx＋ny＝0，则双曲线方程可设为m2x2－n2y2＝λ(λ≠0)．‎