泄露天机金太阳高考押题精粹数学文试题 11页

泄露天机——2012年金太阳高考押题精粹 ‎(数学文课标版)‎ ‎（30道选择题+20道非选择题）‎ 温馨提示：本套试题答案将于5月18号前发至贵校联系邮箱中，请注意查收！如有疑问，请致电：0791—83829122‎ 一．选择题（30道）‎ ‎1．集合,，则等于 A． B． C． D．‎ ‎2．知全集U=R，集合，集合＜＜2，则 A． B． C． D．‎ ‎3．设是实数，且是实数，则 A.1 B. C. D.2‎ ‎4． 是虚数单位，复数，则 A． B． C． D． ‎ ‎5． “a=‎-1”‎是“直线与直线互相垂直”的 A.充分不必要条件 B.必要不充分条件 C.充要条件 C.既不充分也不必要条件 ‎6．已知命题：“，且”，命题：“”。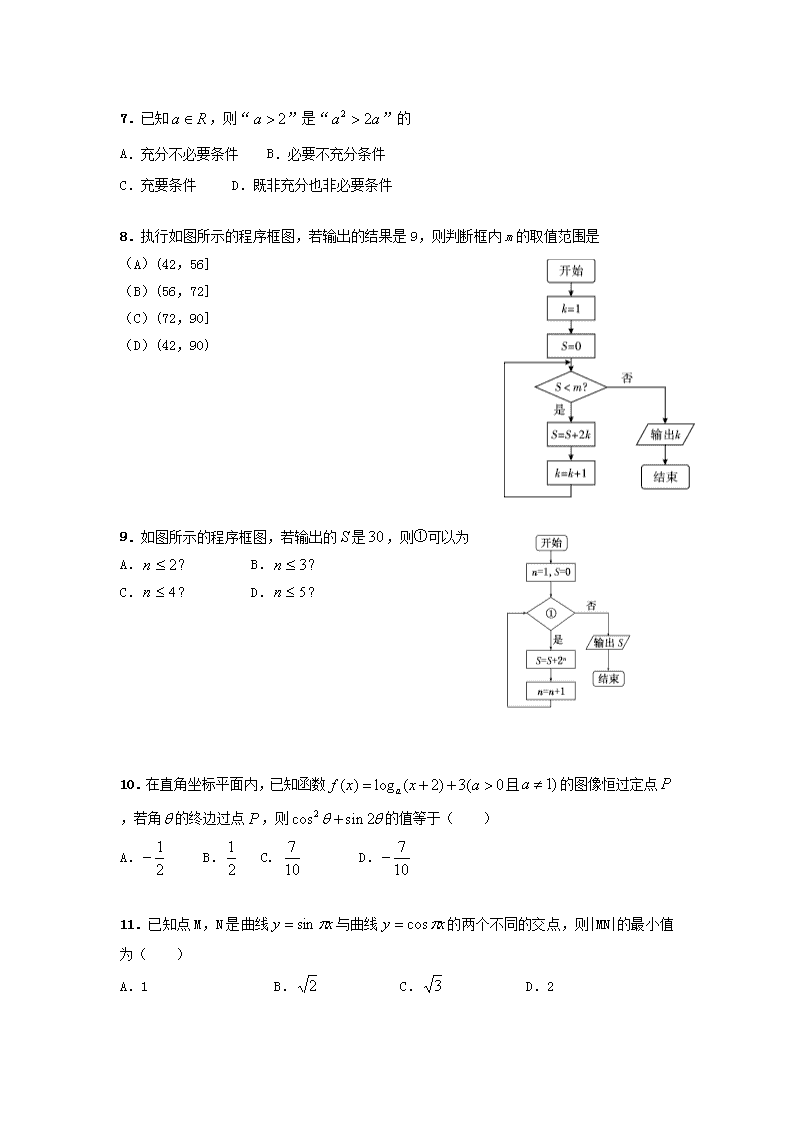则命题是命题的 A．必要不充分条件 B．充分不必要条件 C．充要条件 D．既不充分与不必要条件 ‎7．已知，则“”是“”的 ‎ A．充分不必要条件 B．必要不充分条件 ‎ C．充要条件 D．既非充分也非必要条件 ‎8．执行如图所示的程序框图，若输出的结果是9，则判断框内m的取值范围是 ‎（A）(42，56]‎ ‎（B）(56，72]‎ ‎（C）(72，90]‎ ‎（D）(42，90)‎ ‎9．如图所示的程序框图，若输出的是，则①可以为 ‎ A． B． ‎ C． D．‎ ‎10．在直角坐标平面内，已知函数且的图像恒过定点，若角的终边过点，则的值等于（　　）‎ A． 　 B． C. 　　　　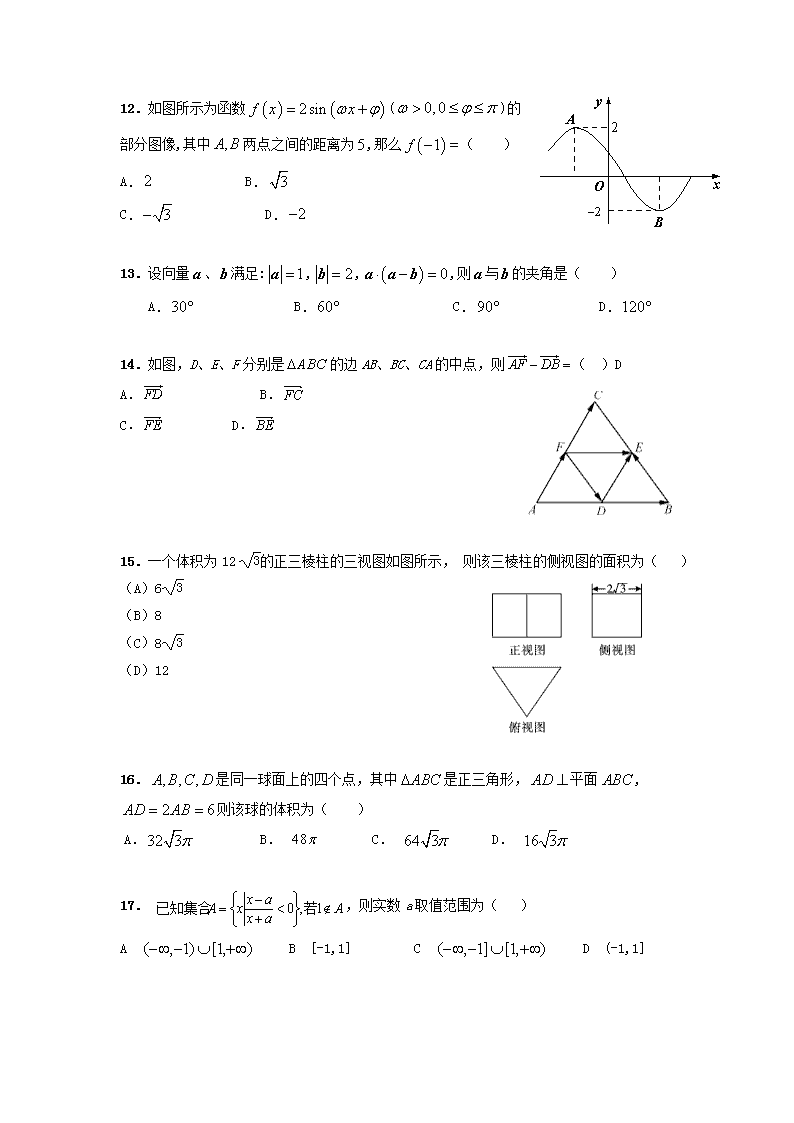D．‎ ‎11．已知点M，N是曲线与曲线的两个不同的交点，则|MN|的最小值为（ ）‎ A．1 B． C． D．2‎ x y O A B ‎12．如图所示为函数()的部分图像,其中两点之间的距离为,那么（ ）‎ A． B． ‎ C． D．‎ ‎13．设向量、满足:,,,则与的夹角是（ ）‎ A． B． C． D． ‎ ‎14．如图，D、E、F分别是的边AB、BC、CA的中点，则（ ）D A． B． ‎ C． D．‎ ‎15．一个体积为12的正三棱柱的三视图如图所示， 则该三棱柱的侧视图的面积为（ ）‎ ‎（A）6 ‎（B）8‎ ‎（C）8 ‎（D）12 ‎ ‎16．是同一球面上的四个点，其中是正三角形，平面,则该球的体积为（ ） ‎ ‎ A． B． C． D． ‎ ‎17． ，则实数a取值范围为（ ）‎ A B [-1,1] C D (-1,1] ‎ ‎18．设,（其中），则大小关系为（　）A． B． ‎ C． D．‎ ‎19．若a是从集合{0，1，2，3}中随机抽取的一个数，b是从集合{0，1，2}中随机抽取的一个数，则关于x的方程有实根的概率是 （ ）‎ A． B． C． D．‎ ‎20．右图是，两组各名同学体重（单位：）‎ 数据的茎叶图．设，两组数据的平均数依次 为和，标准差依次为和，那么（ ）‎ ‎（注：标准差，其中为的平均数）‎ ‎（A）， （B），‎ ‎（C）， （D），‎ ‎21．设Sn是等差数列的前n项和，若 ,则的取值区间为（ ）‎ A. B. [3,4] C. [4,7] D. [3,7]‎ ‎22．若等比数列的前项和，则 A.4 B‎.12 C.24 D.36‎ ‎23．抛物线y2＝2px（p＞0）的焦点为F，点A、B在此抛物线上，且∠AFB＝90°，弦AB的中点M在其准线上的射影为M′，则的最大值为（ ）‎ ‎（A） （B） （C）1 （D） ‎24．已知双曲线的焦点为，点在双曲线上，且，则点 到轴的距离为（ ）‎ A． B． 　 C． 　 D． ‎ ‎25．若直线被所截得的弦长为，则实数的值为（ ）‎ A.或 B.1或‎3 C.或6 D.0或4‎ ‎26．设函数，若f（a）＞1，则实数a的取值范围是（ ）‎ A. 　 B.∪ C.（1，+∞） 　 D.∪（0，+∞） ‎ ‎27．定义在上的函数的图像关于对称，且当时，（其中是的导函数），若，则的大小关系是（ ）‎ A. B. C. D. ‎28．曲线在点（0，1）处的切线方程为( )‎ A． B． C． D．‎ ‎29．函数,的图像可能是下列图像中的（ ）‎ x y O ‎。‎ x y O ‎。‎ x y O ‎。‎ x y O ‎。‎ ‎。‎ ‎。‎ A． B． C． D． ‎ ‎30．设在区间可导，其导数为，给出下列四组条件（ ）‎ ‎①是奇函数，是偶函数 ‎②是以T为周期的函数，是以T为周期的函数 ‎③在区间上为增函数，在恒成立 ‎④在处取得极值，‎ A．①②③ B．①②④ C．①③④ D．②③④‎ 二．填空题（8道）‎ ‎31．已知一组抛物线其中a为2、4中任取的一个数，b为1、3、5中任 取的一个数，从这些抛物线中任意抽取两条，它们在与直线x=l交点处的切线相互平行的概 率是 。‎ ‎32．已知双曲线的两条渐近线均和圆C：x2+y2-6x+5=0相切，且双曲线的右焦点为抛物线的焦点，则该双曲线的标准方程为 . ‎ 正视图 侧视图 俯视图 ‎33．一个几何体的三视图如图所示，则这个几何体的表面积与其外接球面积之比为________. ‎ ‎34．函数f（x）=x3+ax（x∈）在x=l处有极值，则曲线y= f（x）在原点处的切线方程 是_____ ‎ ‎35．△ABC中，若∠A、∠B、∠C所对的边a，b，c均成等差数列，△ABC的面积为，‎ 那么b= 。‎ ‎36．若，则的最大值是_________.‎ ‎37．为了了解“预防禽流感疫苗”的使用情况，某市卫生部门对本地区9月份至11月份注 射疫苗的所有养鸡场进行了调查，根据下图表提供的信息，可以得出这三个月本地区每月注 射了疫苗的鸡的数量平均为 万只。‎ ‎38．记当时，观察下列等式：‎ ‎， ‎ ‎，‎ ‎，‎ ‎，‎ ‎， 可以推测， . ‎ 三．解答题（12道）‎ ‎39．已知函数．]‎ ‎（1）求函数的最小值和最小正周期；‎ ‎（2）设的内角的对边分别为且，，若 ‎，求的值．‎ ‎40．已知各项均不相等的等差数列{an}的前四项和S4＝14，且a1，a3，a7成等比数列．‎ ‎(1)求数列{an}的通项公式；‎ ‎(2)设Tn为数列的前n项和，若Tn≤λan＋1对∀n∈N*恒成立，求实数λ的最小值．‎ ‎41．衡阳市第一次联考后，某校对甲、乙两个文科班的数学考试成绩进行分析，规定：大于或等于120分为优秀，120分以下为非优秀.统计成绩后，得到如下的列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为.‎ 优秀 非优秀 合计 甲班 ‎10‎ 乙班 ‎30‎ 合计 ‎110‎ ⑴请完成上面的列联表；‎ ⑵根据列联表的数据，若按99.9%的可靠性要求，能否认为“成绩与班级有关系”；‎ ⑶若按下面的方法从甲班优秀的学生中抽取一人：把甲班优秀的10名学生从2到11进行编号，先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号.试求抽到9号或10号的概率.‎ 参考公式与临界值表：.‎ ‎0.100‎ ‎0.050‎ ‎0.025‎ ‎0.010‎ ‎0.001‎ ‎2.706‎ ‎3.841‎ ‎5.024‎ ‎6.635‎ ‎10.828‎ ‎42．某校为了解学生的视力情况，随机抽查了一部分学生的视力，将调查结果分组，分组区间为（3.9，4.2]，（4.2，4.5]，…，（5.1，5.4]．经过数据处理，得到如下频率分布表：‎ 分组 频数 频率 ‎（3.9，4.2]‎ ‎3‎ ‎0.06‎ ‎（4.2，4.5]‎ ‎6‎ ‎0.12‎ ‎（4.5，4.8]‎ ‎25‎ x ‎（4.8，5.1]‎ y z ‎（5.1，5.4]‎ ‎2‎ ‎0.04‎ 合计 n ‎1.00‎ ‎（Ⅰ）求频率分布表中未知量n，x，y，z的值；‎ ‎（Ⅱ）从样本中视力在（3.9，4.2]和（5.1，5.4]的所有同学中随机抽取两人，求两人的视力差的绝对值低于0.5的概率．‎ ‎43．如图四棱锥中，底面是平行四边形，，平面，，，是的中点. ‎ ‎(Ⅰ)求证：平面；‎ ‎(Ⅱ)试在线段上确定一点，使∥平面，并求三棱锥-的体积.‎ ‎44．已知椭圆的方程为：，其焦点在轴上，离心率.‎ ‎（1）求该椭圆的标准方程；‎ ‎（2）设动点满足，其中M，N是椭圆上的点，直线OM与ON的斜率之积为，求证：为定值.‎ ‎（3）在（2）的条件下，问：是否存在两个定点，使得为定值？‎ 若存在，给出证明；若不存在，请说明理由. ‎ ‎45．本题主要考查抛物线的标准方程、简单的几何性质等基础知识，考查运算求解、推理论证的能力：‎ F B x y O A C D M N ‎（第45题）‎ 如图，在平面直角坐标系中，抛物线的顶点在原点，焦点为F（1，0）．过抛物线在轴上方的不同两点、作抛物线的切线、，与轴分别交于、两点，且与交于点，直线与直线交于点．‎ ‎（1）求抛物线的标准方程；‎ ‎（2）求证：轴；‎ ‎（3）若直线与轴的交点恰为F（1，0），‎ ‎ 求证：直线过定点．‎ ‎46．已知．‎ ‎(1) 求函数在上的最小值；‎ ‎(2) 对一切，恒成立，求实数a的取值范围；‎ ‎(3) 证明：对一切，都有成立．‎ ‎47．已知函数，‎ ‎（1）时，求的单调区间；‎ ‎（2）若时，函数的图象总在函数的图像的上方，求实数a的取值范围.‎ ‎48．如图，⊙O1与⊙O2相交于A、B两点，过点A作⊙O1的切线交⊙O2于点C，过点B作两圆的割线，分别交⊙O1、⊙O2于点D、E，DE与AC相交于点P．‎ ‎（1）求证：AD//EC；‎ ‎（2）若AD是⊙O2的切线，且PA=6，PC =2，BD =9，求AD的长。‎ ‎49．已知直线为参数), 曲线 （为参数）.‎ ‎（Ⅰ）设与相交于两点,求；‎ ‎（Ⅱ）若把曲线上各点的横坐标压缩为原来的倍,纵坐标压缩为原来的倍,得到曲线,设点是曲线上的一个动点,求它到直线的距离的最小值.‎ ‎50．已知函数 ‎（1）当时，求函数的定义域；‎ ‎（2）若关于的不等式的解集是,求的取值范围.‎