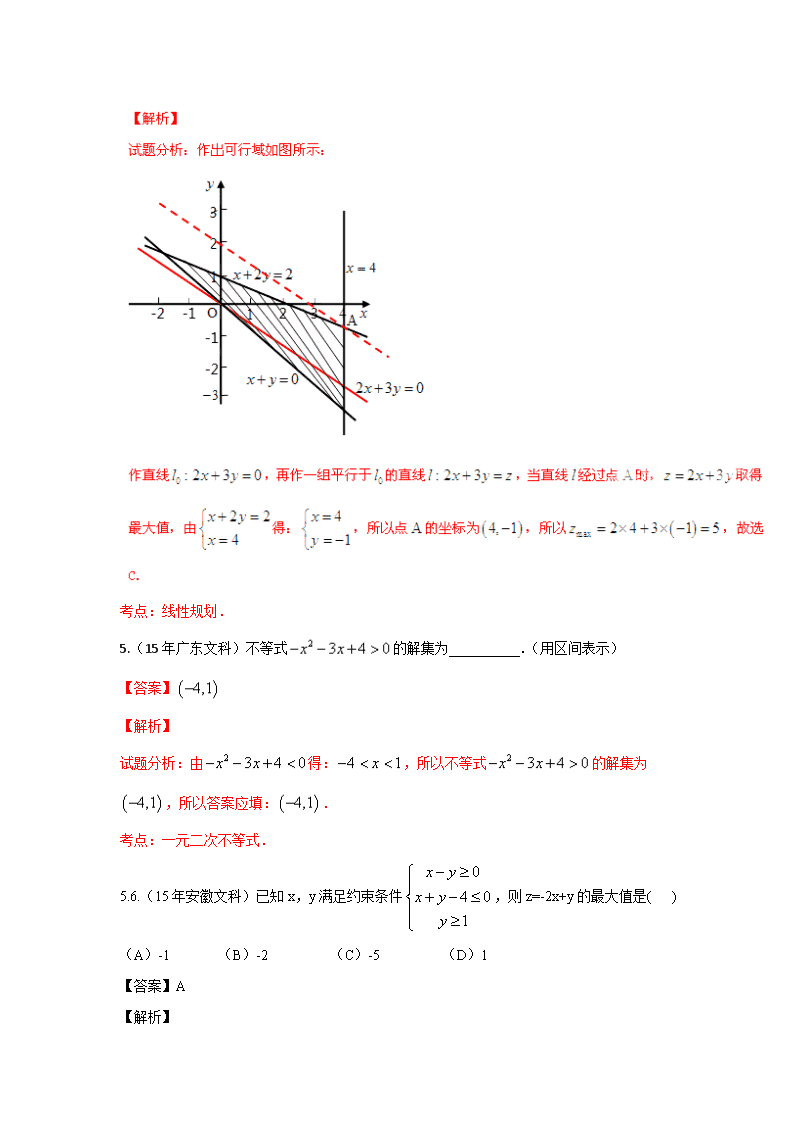- 722.00 KB
- 2021-05-13 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
专题七 不等式
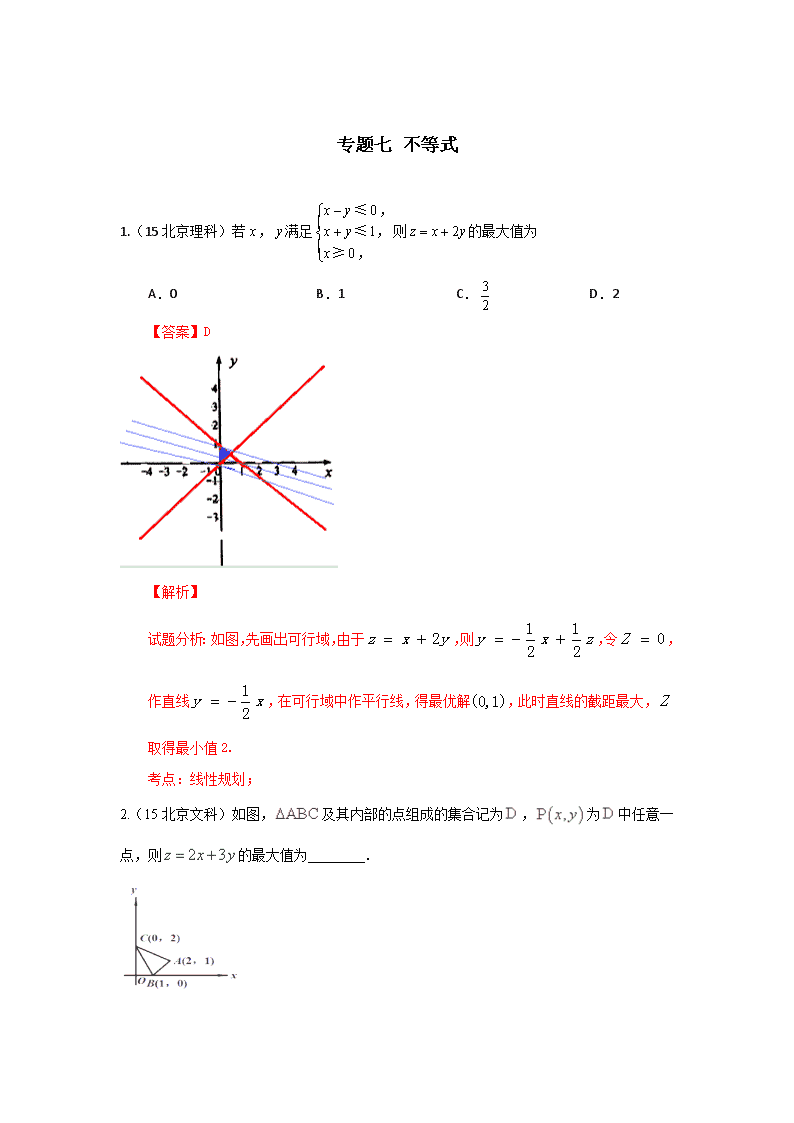
1.(15北京理科)若,满足则的最大值为
A.0 B.1 C. D.2
【答案】D
【解析】
试题分析:如图,先画出可行域,由于,则,令,作直线,在可行域中作平行线,得最优解,此时直线的截距最大,取得最小值2.
考点:线性规划;
2.(15北京文科)如图,及其内部的点组成的集合记为,为中任意一点,则的最大值为 .
【答案】7
考点:线性规划.
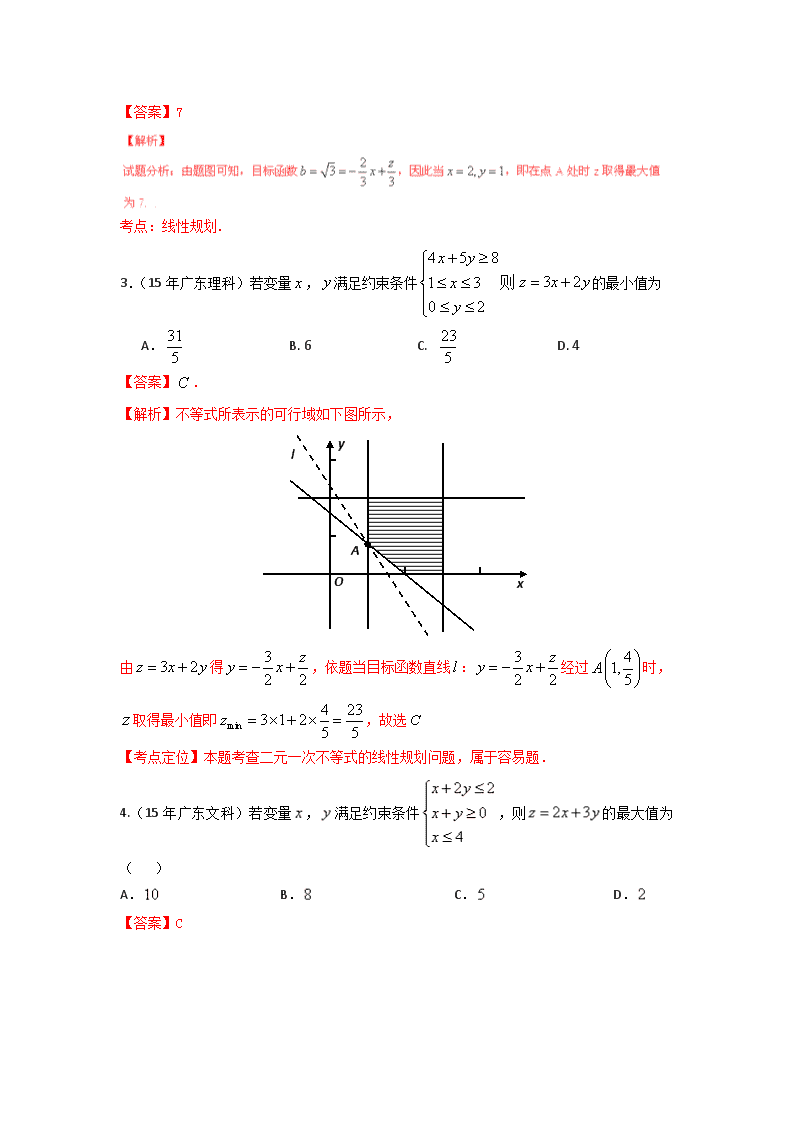
3.(15年广东理科)若变量,满足约束条件则的最小值为
A. B. 6 C. D. 4
【答案】.
【解析】不等式所表示的可行域如下图所示,
x
y
O
A
l
由得,依题当目标函数直线:经过时,取得最小值即,故选
【考点定位】本题考查二元一次不等式的线性规划问题,属于容易题.
4.(15年广东文科)若变量,满足约束条件,则的最大值为( )
A. B. C. D.
【答案】C
考点:线性规划.
5.(15年广东文科)不等式的解集为 .(用区间表示)
【答案】
【解析】
试题分析:由得:,所以不等式的解集为,所以答案应填:.
考点:一元二次不等式.
5. 6.(15年安徽文科)已知x,y满足约束条件,则z=-2x+y的最大值是( )
(A) -1 (B)-2 (C)-5 (D)1
【答案】A
【解析】
试题分析:根据题意作出约束条件确定的可行域,如下图:
令,可知在图中处,取到最大值-1,故选A.
考点:简单的线性规划.
7.(15年福建理科)若变量 满足约束条件 则 的最小值等于 ( )
A. B. C. D.2
【答案】A
【解析】
试题分析:画出可行域,如图所示,目标函数变形为,当最小时,直线的纵截距最大,故将直线经过可行域,尽可能向上移到过点时,取到最小值,最小值为
,故选A.
考点:线性规划.
8.(15年福建理科)已知 ,若 点是 所在平面内一点,且 ,则 的最大值等于( )
A.13 B.15 C.19 D.21
【答案】A
考点:1、平面向量数量积;2、基本不等式.
9.(15年福建文科)若直线过点,则的最小值等于( )
A.2 B.3 C.4 D.5
【答案】C
考点:基本不等式.
10.(15年福建文科)变量满足约束条件,若的最大值为2,则实数等于( )
A. B. C. D.
【答案】C
【解析】
试题分析:将目标函数变形为,当取最大值,则直线纵截距最小,故当时,不满足题意;当时,画出可行域,如图所示, 其中.显然不是最优解,故只能是最优解,代入目标函数得,解得,故选C.
考点:线性规划.
11.(15年新课标1理科)若x,y满足约束条件则的最大值为 .
【答案】3
【解析】作出可行域如图中阴影部分所示,由斜率的意义知,是可行域内一点与原点连线的斜率,由图可知,点A(1,3)与原点连线的斜率最大,故的最大值为3.
12.(15年新课标2理科)若x,y满足约束条件,则的最大值为____________.
【答案】
13.(15年新课标2文科)若x,y满足约束条件 ,则z=2x+y的最大值为 .
【答案】8
考点:线性规划
14.(15年陕西理科)设,若,,,则下列关系
式中正确的是( )
A. B. C. D.
【答案】C
考点:1、基本不等式;2、基本初等函数的单调性.
15.(15年陕西理科)某企业生产甲、乙两种产品均需用A,B两种原料.已知生产1吨每种产品需原料及每天原料
的可用限额如表所示,如果生产1吨甲、乙产品可获利润分别为3万元、4万元,则该企业每天可获得最
大利润为( )
A.12万元 B.16万元 C.17万元 D.18万元
【答案】D
【解析】
试题分析:设该企业每天生产甲、乙两种产品分别为、吨,则利润
由题意可列,其表示如图阴影部分区域:
当直线过点时,取得最大值,所以,故选
D.
考点:线性规划.
16.(15年陕西文科)某企业生产甲乙两种产品均需用A,B两种原料,已知生产1吨每种产品需原料及每天原料的可用限额表所示,如果生产1吨甲乙产品可获利润分别为3万元、4万元,则该企业每天可获得最大利润为( )
A.12万元 B.16万元 C.17万元 D.18万元
【答案】
当直线过点时,取得最大值
故答案选
考点:线性规划.
17.(15年天津理科)设变量 满足约束条件 ,则目标函数的最大值为
(A)3 (B)4 (C)18 (D)40
【答案】C
考点:线性规划.
18.(15年天津文科)设变量满足约束条件,则目标函数的最大值为( )
(A) 7 (B) 8 (C) 9 (D)14
【答案】C
考点:线性规划
19.(15年天津文科)设,则“”是“”的( )
(A) 充分而不必要条件 (B)必要而不充分条件
(C)充要条件 (D)既不充分也不必要条件
【答案】A
【解析】
试题分析:由,可知“”是“”的充分而不必要条件,故选A.
考点:1.不等式;2. 充分条件与必要条件.
20.(15年天津文科)已知 则当a的值为 时
取得最大值.
【答案】4
【解析】
试题分析:当时取等号,结合可得
考点:基本不等式.
21.(15年湖南理科)执行如图1所示的程序框图,如果输入,则输出的( )
A. B. C. D.
时,
的最小值是,故选A.
考点:线性规划.
22.(15年山东理科)不等式的解集是
(A) (B) (C) (D)
解析:当时,成立;当时,,解得,则;当时,不成立.综上,答案选(A)
23.(15年山东理科)已知满足约束条件若的最大值为4,则
(A) (B) (C) (D)
解析:由得,借助图形可知:当,即时在时有最大值0,不符合题意;当,即时在时有最大值,不满足;当,即时在时有最大值,不满足;当,即时在时有最大值,满足;答案选(B)
24.(15年江苏)不等式的解集为________.
【答案】
【解析】
试题分析:由题意得:,解集为
考点:解指数不等式与一元二次不等式
相关文档
- 2018版高考数学(浙江·文理通用)大一2021-05-1318页
- 安徽省芜湖市第一中学高考物理一轮2021-05-137页
- 人教版整理高考英语写作应试技巧2021-05-1310页
- 2020 年中考语文一模试卷精选汇编 2021-05-135页
- 2019高考物理一轮复习 第六章 第12021-05-132页
- (浙江选考)2020版高考化学 考前提升2021-05-137页
- 高考数学公式 皇牌大放送2021-05-1331页
- 高考地理二轮复习图表专项训练12021-05-133页
- 2020版高考历史一轮复习 专题1 君2021-05-1311页
- 高考地理一轮复习限时规范训练28地2021-05-138页