2020版高考物理总复习 第19课 动量守恒定律 碰撞练习 5页

第19课 动量守恒定律 碰撞 ‎1．系统动量是否守恒的判断 ‎(1)(多选)(经典题，6分) 如图所示，A、B 两物体的质量 mA>mB，中间用一段细绳相连并有一被压缩的弹簧，放在平板小车C上后，A、B、C 均处于静止状态。若地面光滑，则在细绳被剪断后，A、B 从C 上滑离之前，A、B 在 C 上向相反方向滑动过程中(　　)‎ A．若A、B与C之间的摩擦力大小相同，则A、B组成的系统动量守恒，A、B、C组成的系统动量也守恒 B．若A、B与C之间的摩擦力大小不相同，则A、B组成的系统动量不守恒，A、B、C组成的系统动量也不守恒 C．若A、B与C之间的摩擦力大小不相同，则A、B组成的系统动量不守恒，但A、B、C组成的系统动量守恒 D．以上说法均不对 答案：AC 解析：当A、B两物体组成一个系统时，弹簧的弹力为内力，而A、B与C之间的摩擦力为外力。当A、B与C之间的摩擦力等大、反向时，A、B组成的系统所受外力之和为零，动量守恒。当A、B与C之间的摩擦力大小不相等时，A、B组成的系统所受外力之和不为零，动量不守恒。而对于A、B、C组成的系统，由于弹簧的弹力及A、B与C之间的摩擦力均为内力，故不论A、B与C之间的摩擦力的大小是否相等，A、B、C组成的系统所受外力之和均为零，故系统的动量守恒，故A项、C项均正确，B项、D项均错误。‎ ‎2．动量守恒定律的应用 a．“人船”模型 ‎(2)(经典题，8分) 长为L、质量为m2的船停在平静水面上，一个质量为m1的人静立在船头，若不计水的阻力，当人从船头走到船尾的过程中，船和人对地面的位移各是多少？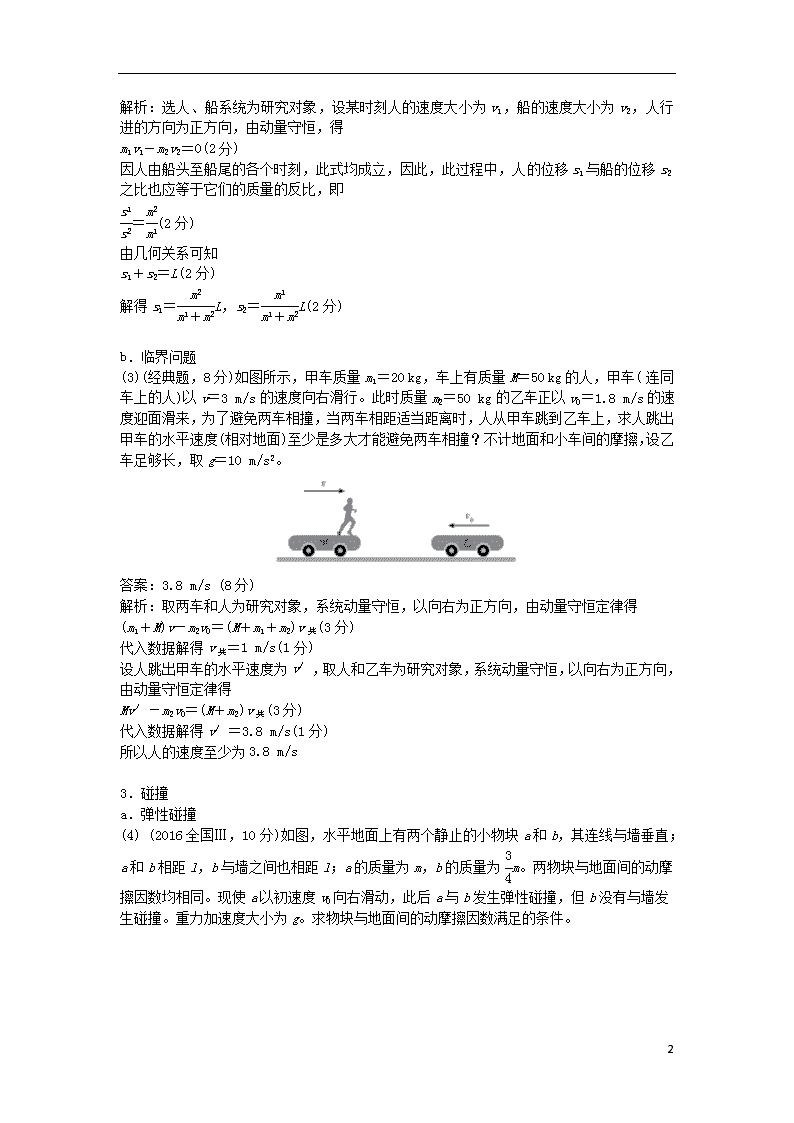‎ 答案：s1＝L，s2＝L(8分)‎ 5‎ 解析：选人、船系统为研究对象，设某时刻人的速度大小为v1，船的速度大小为v2，人行进的方向为正方向，由动量守恒，得 m1v1－m2v2＝0(2分)‎ 因人由船头至船尾的各个时刻，此式均成立，因此，此过程中，人的位移s1与船的位移s2之比也应等于它们的质量的反比，即 ＝(2分)‎ 由几何关系可知 s1＋s2＝L(2分)‎ 解得s1＝L，s2＝L(2分)‎ b．临界问题 ‎(3)(经典题，8分)如图所示，甲车质量m1＝‎20 kg，车上有质量M＝‎50 kg的人，甲车( 连同车上的人)以v＝‎3 m/s的速度向右滑行。此时质量m2＝‎50 kg的乙车正以v0＝‎1.8 m/s的速度迎面滑来，为了避免两车相撞，当两车相距适当距离时，人从甲车跳到乙车上，求人跳出甲车的水平速度(相对地面)至少是多大才能避免两车相撞？不计地面和小车间的摩擦，设乙车足够长，取g＝‎10 m/s2。‎ 答案：‎3.8 m/s (8分)‎ 解析：取两车和人为研究对象，系统动量守恒，以向右为正方向，由动量守恒定律得 ‎(m1＋M)v－m2v0＝(M＋m1＋m2)v共(3分)‎ 代入数据解得v共＝‎1 m/s(1分)‎ 设人跳出甲车的水平速度为v′，取人和乙车为研究对象，系统动量守恒，以向右为正方向，由动量守恒定律得 Mv′－m2v0＝(M＋m2)v共(3分)‎ 代入数据解得v′＝‎3.8 m/s(1分)‎ 所以人的速度至少为‎3.8 m/s ‎3．碰撞 a．弹性碰撞 ‎(4) (2016全国Ⅲ，10分)如图，水平地面上有两个静止的小物块a和b，其连线与墙垂直；a和b相距l，b与墙之间也相距l；a的质量为m，b的质量为m。两物块与地面间的动摩擦因数均相同。现使a以初速度v0向右滑动，此后a与b发生弹性碰撞，但b没有与墙发生碰撞。重力加速度大小为g。求物块与地面间的动摩擦因数满足的条件。‎ 5‎ 答案：≤μ<(10分)‎ 解析：设物块与地面间的动摩擦因数为μ。若要物块a、b能够发生碰撞，应有 mv>μmgl①(1分)‎ 即μ<②(1分)‎ 设在a、b发生弹性碰撞前的瞬间，a的速度大小为v1。由能量守恒定律得 mv＝mv＋μmgl③(2分)‎ 设在a、b碰撞后的瞬间，a、b的速度大小分别为v1′、v2′，由动量守恒和能量守恒有 mv1＝mv1′＋mv2′④(1分)‎ mv＝mv1′2＋·v2′2⑤(1分)‎ ‎④⑤联立解得 v2′＝v1⑥(1分)‎ 由题意，b没有与墙发生碰撞，由功能关系可知 ·v2′2≤μ·gl⑦(1分)‎ ‎③⑥⑦联立解得 μ≥⑧(2分)‎ 联立②⑧式，a与b发生碰撞、但b没有与墙发生碰撞的条件为 ≤μ<⑨‎ b．完全非弹性碰撞 ‎(5)(经典题，10分)如图所示，光滑的杆MN水平固定，物块A穿在杆上，可沿杆无摩擦滑动，A通过长度为L的轻质细绳与物块B相连，A、B质量均为m且可视为质点。一质量也为m的子弹水平射入物块B后未穿出，若杆足够长，此后运动过程中绳子偏离竖直方向的最大夹角为60°。求子弹刚要射入物块B时的速度大小。‎ 5‎ 答案：2(10分)‎ 解析：子弹射入物块B的过程，子弹和物块B组成的系统水平方向动量守恒 mv0＝2mv1(3分)‎ 子弹开始射入物块B到细绳偏离竖直方向夹角最大的过程，子弹和两物块组成的系统水平方向动量守恒 mv0＝3mv2(2分)‎ 据能量关系可得 ‎2mgL(1－cos 60°)＝×2mv－×3mv(3分)‎ 解得v0＝2 (2分)‎ c．“类碰撞”问题 ‎(6)(经典题，10分)如图，放置在光滑水平面上两物体A、B的质量分别为m1、m2，它们间用一轻弹簧连接，今突然给A一个冲量，使A具有速度v0，向右运动，求：‎ ‎①弹簧的压缩量最大时，A、B的速度分别为多大？弹簧弹性势能多大？‎ ‎②当弹簧第一次恢复原长时，A、B的速度为多少？‎ 答案：①，·m1v(5分)　‎ ‎②v0，v0(5分)‎ 解析：①弹簧的压缩量最大时A、B两物体的速度相等，根据动量守恒有 m1v0＝(m1＋m2)v(2分)‎ 解得v＝(1分)‎ 此时系统动能损失为 ΔEk＝m1v－(m1＋m2)v2(1分)‎ 解得Ep＝ΔEk＝·m1v(1分)‎ ‎②从弹簧为原长到弹簧第一次恢复原长，系统水平方向的动量守恒，且初末状态系统的动能无损失，所以，可将这个过程看成完全弹性碰撞，根据动量守恒和能量守恒有 m1v0＝m1v1＋m2v2(2分)‎ m1v＝m1v＋m2v(2分)‎ 解得A、B两物体的速度为 5‎ v1＝v0，v2＝v0(1分)‎ ‎4．碰撞可能性的判断 ‎(7)(经典题，3分)甲、乙两球在光滑水平面上沿同一直线、同一方向运动，甲球的动量是p1＝‎5 kg·m/s，乙球的动量是p2＝‎7 kg·m/s，当甲球追上乙球发生碰撞后，乙球的动量变为p2′＝‎10 kg·m/s，设甲球的质量为m1，乙球的质量为m2，则m1、m2的关系可能是(　　)‎ A．m1＝m2 B．‎2m1＝m2‎ C．‎4m1＝m2 D．‎6m1＝m2‎ 答案：C 解析： 碰撞过程中动量守恒，可知碰撞后甲球的动量p′1＝‎2 kg·m/s。由于是甲追碰乙，碰撞前甲的速度大于乙的速度，有>，可得m2>m1。碰撞后甲的速度不大于乙的速度，有≤，可得m2≤‎5m1。碰撞后系统的动能不大于碰撞前系统的动能，由Ek＝可知，＋≤＋，解得m2≥m1。联立解得m1≤m2≤‎5m1，故C项正确。‎ 5‎