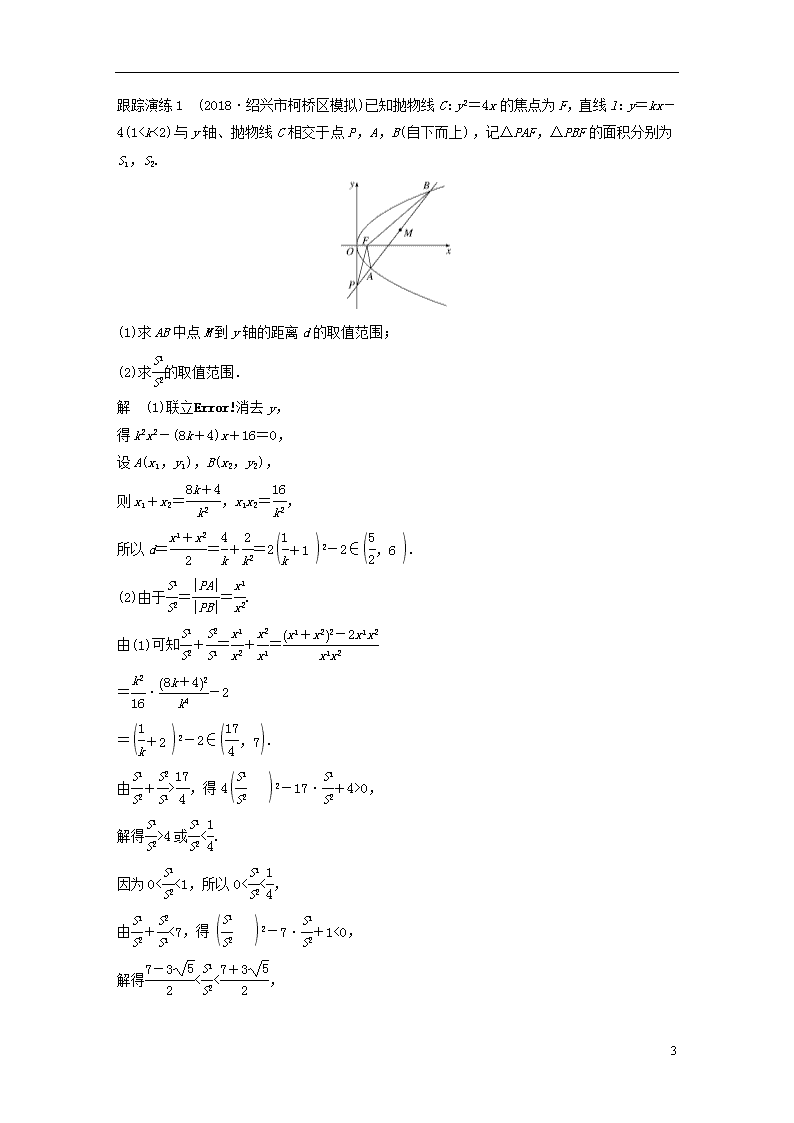2020高考数学二轮复习 专题四 解析几何 第3讲 圆锥曲线的综合问题学案 19页

第3讲　圆锥曲线的综合问题 ‎[考情考向分析]　1.圆锥曲线的综合问题一般以直线和圆锥曲线的位置关系为载体，以参数处理为核心，考查范围、最值问题，定点、定值问题，探索性问题.2.试题解答往往要综合应用函数与方程、数形结合、分类讨论等多种思想方法，对计算能力也有较高要求，难度较大．‎ 热点一　范围、最值问题 圆锥曲线中的范围、最值问题，可以转化为函数的最值问题(以所求式子或参数为函数值)，或者利用式子的几何意义求解．‎ 例1　(2018·浙江省稽阳联谊学校联考)已知离心率为的椭圆C：＋＝1(a>b>0)过点P，与坐标轴不平行的直线l与椭圆C交于A，B两点，其中M为A关于y轴的对称点，N(0，)，O为坐标原点．‎ ‎(1)求椭圆C的方程；‎ ‎(2)分别记△PAO，△PBO的面积为S1，S2，当M，N，B三点共线时，求S1·S2的最大值．‎ 解　(1)∵＝，a2＝b2＋c2，∴a＝2b.‎ 19‎ 把点P代入椭圆方程可得＋＝1，‎ 解得a＝2，b＝1，∴椭圆方程为＋y2＝1.‎ ‎(2)设点A坐标为(x1，y1)，点B坐标为(x2，y2)，‎ 则M为(－x1，y1)，‎ 设直线l的方程为y＝kx＋b，‎ 联立椭圆方程可得(4k2＋1)x2＋8kbx＋4b2－4＝0，‎ ‎∴x1＋x2＝，x1x2＝，Δ>0，‎ ‎∵M，N，B三点共线，‎ ‎∴kMN＝kBN，‎ 即＋＝0，‎ 化简得8k(1－b)＝0，‎ 解得b＝或k＝0(舍去)．‎ 设A，B两点到直线OP的距离分别为d1，d2.‎ 直线OP的方程为x－2y＝0，|OP|＝，‎ ‎∴S1·S2＝|(x1－2y1)(x2－2y2)|，‎ 化简可得 S1·S2＝|(2k－)2x1x2＋(2k－)(x1＋x2)＋2|‎ ‎＝.‎ 又∈∪，‎ ‎∴当k＝－时，S1·S2的最大值为.‎ 思维升华　解决范围问题的常用方法 ‎(1)数形结合法：利用待求量的几何意义，确定出极端位置后，利用数形结合法求解．‎ ‎(2)构建不等式法：利用已知或隐含的不等关系，构建以待求量为元的不等式求解．‎ ‎(3)构建函数法：先引入变量构建以待求量为因变量的函数，再求其值域．‎ 跟踪演练1　(2018·绍兴市柯桥区模拟)已知抛物线C：y2＝4x的焦点为F，直线l：y＝kx－4(1，得42－17·＋4>0，‎ 解得>4或<.‎ 因为0<<1，所以0<<，‎ 由＋<7，得2－7·＋1<0，‎ 解得<<，‎ 因此<<.‎ 即的取值范围为.‎ 热点二　定点、定值问题 19‎ ‎1．由直线方程确定定点，若得到了直线方程的点斜式：y－y0＝k(x－x0)，则直线必过定点(x0，y0)；若得到了直线方程的斜截式：y＝kx＋m，则直线必过定点(0，m)．‎ ‎2．解析几何中的定值问题是指某些几何量(线段的长度、图形的面积、角的度数、直线的斜率等)的大小或某些代数表达式的值等与题目中的参数无关，不依参数的变化而变化，而始终是一个确定的值．‎ 例2　(2018·北京)已知抛物线C：y2＝2px经过点P(1,2)，过点Q(0,1)的直线l与抛物线C有两个不同的交点A，B，且直线PA交y轴于M，直线PB交y轴于N.‎ ‎(1)求直线l的斜率的取值范围；‎ ‎(2)设O为原点，＝λ，＝μ，求证：＋为定值．‎ ‎(1)解　因为抛物线y2＝2px过点(1,2)，‎ 所以2p＝4，即p＝2.‎ 故抛物线C的方程为y2＝4x.‎ 由题意知，直线l的斜率存在且不为0.‎ 设直线l的方程为y＝kx＋1(k≠0)，‎ 由得k2x2＋(2k－4)x＋1＝0.‎ 依题意知Δ＝(2k－4)2－4×k2×1>0，‎ 解得k<0或00)的焦点F，与抛物线Γ相交于A，B两点，且|AB|＝8.‎ ‎(1)求抛物线Γ的方程；‎ ‎(2)过点P(12,8)的两条直线l1，l2分别交抛物线Γ于点C，D和E，F，线段CD和EF的中点分别为M，N.如果直线l1与l2的倾斜角互余，求证：直线MN经过一定点．‎ ‎(1)解　由题意可设直线AB的方程为y＝x－，‎ 由消去y整理得x2－3px＋＝0，‎ Δ＝9p2－4×＝8p2>0，‎ 令A(x1，y1)，B(x2，y2)，‎ 则x1＋x2＝3p，‎ 由抛物线的定义得|AB|＝x1＋x2＋p＝4p＝8，‎ ‎∴p＝2.‎ ‎∴抛物线的方程为y2＝4x.‎ ‎(2)证明　设直线l1，l2的倾斜角分别为α，β，‎ 由题意知，α，β≠.‎ 直线l1的斜率为k，则k＝tan α.‎ ‎∵直线l1与l2的倾斜角互余，‎ 19‎ ‎∴tan β＝tan＝ ‎＝＝＝，‎ ‎∴直线l2的斜率为.‎ ‎∴直线CD的方程为y－8＝k(x－12)，‎ 即y＝k(x－12)＋8.‎ 由 消去x整理得ky2－4y＋32－48k＝0，‎ 设C(xC，yC)，D(xD，yD)，‎ ‎∴yC＋yD＝，‎ ‎∴xC＋xD＝24＋－，‎ ‎∴点M的坐标为.‎ 以代替点M坐标中的k，‎ 可得点N的坐标为(12＋2k2－8k,2k)，‎ ‎∴kMN＝＝.‎ ‎∴直线MN的方程为 y－2k＝[x－(12＋2k2－8k)]，‎ 即y＝x－10，‎ 显然当x＝10时，y＝0，‎ 故直线MN经过定点.‎ 热点三　探索性问题 19‎ ‎1．解析几何中的探索性问题，从类型上看，主要是存在类型的相关题型，解决这类问题通常采用“肯定顺推法”，将不确定性问题明确化．其步骤为：假设满足条件的元素(点、直线、曲线或参数)存在，用待定系数法设出，列出关于待定系数的方程组，若方程组有实数解，则元素(点、直线、曲线或参数)存在；否则，元素(点、直线、曲线或参数)不存在．‎ ‎2．反证法与验证法也是求解存在性问题常用的方法．‎ 例3　已知椭圆C：＋＝1(a>b>0)的上、下焦点分别为F1，F2，上焦点F1到直线4x＋3y＋12＝0的距离为3，椭圆C的离心率e＝.‎ ‎(1)求椭圆C的方程；‎ ‎(2)椭圆E：＋＝1，设过点M(0,1)，斜率存在且不为0的直线交椭圆E于A，B两点，试问y轴上是否存在点P，使得＝λ？若存在，求出点P的坐标；若不存在，说明理由．‎ 解　(1)由已知椭圆C的方程为＋＝1(a>b>0)，‎ 设椭圆的焦点F1(0，c)，‎ 由F1到直线4x＋3y＋12＝0的距离为3，‎ 得＝3，‎ 又椭圆C的离心率e＝，所以＝，‎ 又a2＝b2＋c2，求得a2＝4，b2＝3.‎ 椭圆C的方程为＋＝1.‎ ‎(2)存在．理由如下：由(1)得椭圆E：＋＝1，‎ 设直线AB的方程为y＝kx＋1(k≠0)，‎ 联立 消去y并整理得(4k2＋1)x2＋8kx－12＝0，‎ Δ＝(8k)2＋4(4k2＋1)×12＝256k2＋48>0.‎ 设A(x1，y1)，B(x2，y2)，‎ 则x1＋x2＝－，x1x2＝－.‎ 假设存在点P(0，t)满足条件，‎ 由于＝λ，‎ 19‎ 所以PM平分∠APB.‎ 所以直线PA与直线PB的倾斜角互补，‎ 所以kPA＋kPB＝0.‎ 即＋＝0，‎ 即x2(y1－t)＋x1(y2－t)＝0.(*)‎ 将y1＝kx1＋1，y2＝kx2＋1代入(*)式，‎ 整理得2kx1x2＋(1－t)(x1＋x2)＝0，‎ 所以－2k·＋＝0，‎ 整理得3k＋k(1－t)＝0，即k(4－t)＝0，‎ 因为k≠0，所以t＝4.‎ 所以存在点P(0,4)，使得＝λ.‎ 思维升华　解决探索性问题的注意事项 存在性问题，先假设存在，推证满足条件的结论，若结论正确则存在，若结论不正确则不存在．‎ ‎(1)当条件和结论不唯一时，要分类讨论．‎ ‎(2)当给出结论而要推导出存在的条件时，先假设成立，再推出条件．‎ ‎(3)当条件和结论都不知，按常规方法解题很难时，要思维开放，采取另外的途径．‎ 跟踪演练3　已知椭圆C：＋＝1(a>b>0)经过点M(2，)，且离心率为.‎ ‎(1)求a，b的值，并写出椭圆C的方程；‎ ‎(2)设A，B分别为椭圆C的左、右顶点，在椭圆C上有异于A，B的动点P，若直线PA，PB与直线l：x＝m(m为常数)分别交于不同的两点M，N，则当点P运动时，以MN为直径的圆是否经过定点？‎ 解　(1)由题知，＋＝1，＝，a2＝b2＋c2，‎ 解得a＝2，b＝2，‎ ‎∴椭圆C的方程为＋＝1.‎ ‎(2)由(1)知，A(－2，0)，B(2，0)，‎ 设直线PA，PB的斜率分别为k1，k2，‎ 则直线PA，PB的方程分别为y＝k1(x＋2)，‎ y＝k2(x－2)，‎ 19‎ ‎∴M(m，k1(m＋2))，N(m，k2(m－2))，‎ ‎∴根据射影定理知，以MN为直径的圆的方程为(x－m)2＋[y－k1(m＋2)][y－k2(m－2)]＝0，‎ 即(x－m)2＋y2－[k1(m＋2)＋k2(m－2)]y＋k1k2·(m2－8)＝0，‎ 设点P(x0，y0)，则＋＝1，y＝4，‎ ‎∴k1k2＝·＝＝－，‎ ‎∴(x－m)2＋y2－[k1(m＋2)＋k2(m－2)]y－(m2－8)＝0，‎ 由y＝0，得(x－m)2－(m2－8)＝0，‎ ‎∴(x－m)2＝(m2－8)．‎ 当m2－8<0，即－20.‎ 设A(x1，y1)，B(x2，y2)，则x1＋x2＝，x1x2＝1，‎ 所以|AB|＝·|x1－x2|‎ ‎＝· ‎＝· ‎＝.‎ 同理可得|DE|＝4(1＋k2)．‎ 所以|AB|＋|DE|＝＋4(1＋k2)‎ ‎＝4 ‎＝8＋4≥8＋4×2＝16，‎ 当且仅当k2＝，即k＝±1时，取得等号．‎ ‎2．(2018·浙江)如图，已知点P是y轴左侧(不含y轴)一点，抛物线C：y2＝4x上存在不同的两点A，B满足PA，PB的中点均在C上．‎ ‎(1)设AB中点为M，证明：PM垂直于y轴；‎ ‎(2)若P是半椭圆x2＋＝1(x<0)上的动点，求△PAB面积的取值范围．‎ ‎(1)证明　设P(x0，y0)，A，B.‎ 因为PA，PB的中点在抛物线上，所以y1，y2为方程2＝4·，‎ 即y2－2y0y＋8x0－y＝0的两个不同的实根．‎ 所以y1＋y2＝2y0，‎ 所以PM垂直于y轴．‎ 19‎ ‎(2)解　由(1)可知 所以|PM|＝(y＋y)－x0＝y－3x0，‎ ‎|y1－y2|＝2.‎ 所以△PAB的面积S△PAB＝|PM|·|y1－y2|＝(y－4x0).‎ 因为x＋＝1(－1≤x0<0)，‎ 所以y－4x0＝－4x－4x0＋4∈[4,5]，‎ 所以△PAB面积的取值范围是.‎ 押题预测 已知椭圆C1：＋＝1(a>0)与抛物线C2：y2＝2ax相交于A，B两点，且两曲线的焦点F重合．‎ ‎(1)求C1，C2的方程；‎ ‎(2)若过焦点F的直线l与椭圆分别交于M，Q两点，与抛物线分别交于P，N两点，是否存在斜率为k(k≠0)的直线l，使得＝2？若存在，求出k的值；若不存在，请说明理由．‎ 押题依据　本题将椭圆和抛物线联合起来设置命题，体现了对直线和圆锥曲线位置关系的综合考查．关注知识交汇，突出综合应用是高考的特色．‎ 解　(1)因为C1，C2的焦点重合，‎ 所以＝，‎ 所以a2＝4.‎ 又a>0，所以a＝2.‎ 于是椭圆C1的方程为＋＝1，‎ 抛物线C2的方程为y2＝4x.‎ ‎(2)假设存在直线l使得＝2，‎ 当l⊥x轴时，|MQ|＝3，|PN|＝4，不符合题意，‎ ‎∴直线l的斜率存在，‎ ‎∴可设直线l的方程为y＝k(x－1)(k≠0)，P(x1，y1)，Q(x2，y2)，M(x3，y3)，N(x4，y4)．‎ 由可得k2x2－(2k2＋4)x＋k2＝0，‎ 则x1＋x4＝，x1x4＝1，且Δ＝16k2＋16>0，‎ 所以|PN|＝· 19‎ ‎＝.‎ 由可得(3＋4k2)x2－8k2x＋4k2－12＝0，‎ 则x2＋x3＝，x2x3＝，‎ 且Δ＝144k2＋144>0，‎ 所以|MQ|＝·＝.‎ 若＝2，则＝2×，‎ 解得k＝±.‎ 故存在斜率为k＝±的直线l，使得＝2.‎ A组　专题通关 ‎1．已知椭圆＋＝1(a>b>0)的离心率e＝，左、右焦点分别为F1，F2，且F2与抛物线y2＝4x的焦点重合．‎ ‎(1)求椭圆的标准方程；‎ ‎(2)若过F1的直线交椭圆于B，D两点，过F2的直线交椭圆于A，C两点，且AC⊥BD，求|AC|＋|BD|的最小值．‎ 解　(1)抛物线y2＝4x的焦点坐标为(1,0)，所以c＝1，‎ 又因为e＝＝＝，所以a＝，‎ 所以b2＝2，所以椭圆的标准方程为＋＝1.‎ ‎(2)①当直线BD的斜率k存在且k≠0时，‎ 直线BD的方程为y＝k(x＋1)，‎ 代入椭圆方程＋＝1，‎ 并化简得x2＋6k2x＋3k2－6＝0.‎ Δ＝36k4－4(3k2＋2)(3k2－6)＝48(k2＋1)>0恒成立．‎ 设B(x1，y1)，D(x2，y2)，‎ 则x1＋x2＝－，x1x2＝，‎ ‎|BD|＝·|x1－x2|‎ 19‎ ‎＝＝.‎ 由题意知AC的斜率为－，‎ 所以|AC|＝＝.‎ ‎|AC|＋|BD|＝4 ‎＝≥ ‎＝＝.‎ 当且仅当3k2＋2＝2k2＋3，即k＝±1时，上式取等号，‎ 故|AC|＋|BD|的最小值为.‎ ‎②当直线BD的斜率不存在或等于零时，‎ 可得|AC|＋|BD|＝>.‎ 综上，|AC|＋|BD|的最小值为.‎ ‎2．(2018·诸暨市适应性考试)已知F是抛物线C：x2＝2py(p>0)的焦点，过F的直线交抛物线C于不同的两点A(x1，y1)，B(x2，y2)，且x1x2＝－1.‎ ‎(1)求抛物线C的方程；‎ ‎(2)过点B作x轴的垂线交直线AO(O为坐标原点)于点D，过点A作直线DF的垂线与抛物线C的另一交点为E，AE的中点为G.‎ ‎①求点D的纵坐标；‎ ‎②求的取值范围．‎ 解　(1)设AB：y＝kx＋，‎ 联立得x2＝2p，‎ 即x2－2pkx－p2＝0，‎ ‎∴x1x2＝－p2＝－1，∴p＝1，‎ ‎∴抛物线C的方程为x2＝2y.‎ 19‎ ‎(2)①直线OA的方程为y＝x＝x，‎ ‎∴D，即D，‎ ‎∴点D的纵坐标为－.‎ ‎②∵kDF＝－，∴kAE＝x2，‎ 即直线AE的方程为y－y1＝x2(x－x1)，‎ 联立得－x2x－y1－1＝0，‎ ‎∴xE＝2x2－x1，∴G(x2,2y2＋y1＋1)．‎ ‎∴G，B，D三点共线，∴＝，‎ ‎∵y1·y2＝，‎ ‎∴＝2－＝2－ ‎＝2－∈(1,2)，‎ ‎∴∈.‎ ‎3．(2018·全国Ⅲ)已知斜率为k的直线l与椭圆C：＋＝1交于A，B两点，线段AB的中点为M(1，m)(m>0)．‎ ‎(1)证明：k<－；‎ ‎(2)设F为C的右焦点，P为C上一点，且＋＋＝0.证明：||，||，||成等差数列，并求该数列的公差．‎ ‎(1)证明　设A(x1，y1)，B(x2，y2)，‎ 则＋＝1，＋＝1.‎ 两式相减，并由＝k，得＋·k＝0.‎ 由题设知＝1，＝m，于是k＝－.①‎ 19‎ 由题设得0b>0)的上顶点为点D，右焦点为F2(1,0)，延长DF2交椭圆C于点E，且满足|DF2|＝3|F2E|.‎ ‎(1)求椭圆C的标准方程；‎ ‎(2)过点F2作与x轴不重合的直线l和椭圆C交于A，B两点，设椭圆C的左顶点为点H，且直线HA，HB分别与直线x＝3交于M，N两点，记直线F‎2M，F2N的斜率分别为k1，k2，则k1与k2之积是否为定值？若是，求出该定值；若不是，请说明理由．‎ 解　(1)椭圆C的上顶点为D，右焦点F2(1,0)，点E的坐标为(x，y)．‎ ‎∵|DF2|＝3|F2E|，可得＝3，‎ 又＝，＝，‎ ‎∴代入＋＝1，‎ 可得＋＝1，‎ 19‎ 又a2－b2＝1，解得a2＝2，b2＝1，‎ 即椭圆C的标准方程为＋y2＝1.‎ ‎(2)设A(x1，y1)，B(x2，y2)，H，M，‎ N.‎ 由题意可设直线AB的方程为x＝my＋1，‎ 联立消去x，‎ 得y2＋2my－1＝0，‎ Δ＝‎4m2‎＋4(m2＋2)>0恒成立．‎ ‎∴ 根据H，A，M三点共线，可得＝，‎ ‎∴yM＝.‎ 同理可得yN＝，‎ ‎∴M，N的坐标分别为，，‎ ‎∴k1k2＝·＝yMyN ‎＝·· ‎＝ ‎＝ ‎＝ ‎＝＝.‎ ‎∴k1与k2之积为定值，且该定值是.‎ ‎6．已知平面上动点P到点F的距离与到直线x＝的距离之比为，记动点P 19‎ 的轨迹为曲线E.‎ ‎(1)求曲线E的方程；‎ ‎(2)设M是曲线E上的动点，直线l的方程为mx＋ny＝1.‎ ‎①设直线l与圆x2＋y2＝1交于不同两点C，D，求|CD|的取值范围；‎ ‎②求与动直线l恒相切的定椭圆E′的方程，并探究：若M是曲线Γ：Ax2＋By2＝1上的动点，是否存在与直线l：mx＋ny＝1恒相切的定曲线Γ′？若存在，直接写出曲线Γ′的方程；若不存在，说明理由．‎ 解　(1)设P(x，y)，由题意，得＝.‎ 整理，得＋y2＝1，∴曲线E的方程为＋y2＝1.‎ ‎(2)①圆心到直线l的距离d＝，‎ ‎∵直线与圆有两个不同交点C，D，‎ ‎∴|CD|2＝4.‎ 又∵＋n2＝1(m≠0)，‎ ‎∴|CD|2＝4.‎ ‎∵|m|≤2，∴0