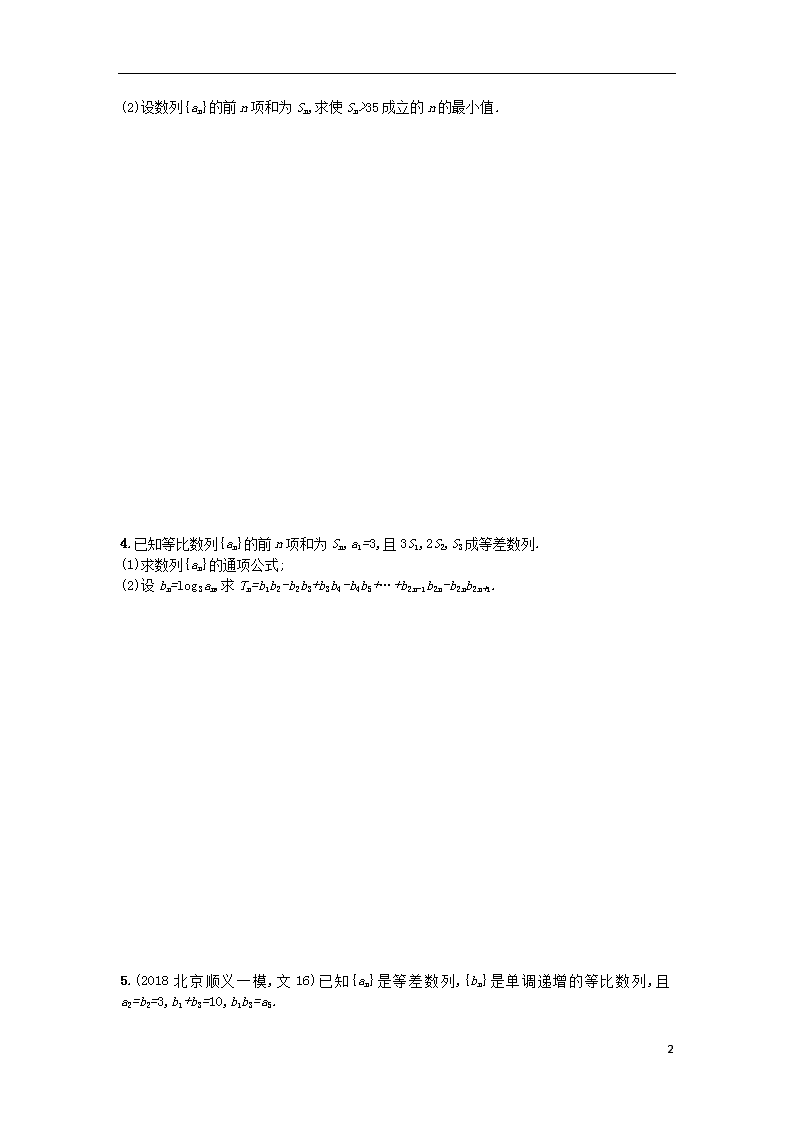2020版高考数学二轮复习 专题四 数列 专题突破练12 等差、等比数列的综合问题 文 7页

专题突破练12　等差、等比数列的综合问题 ‎1.(2018北京东城一模,文15)已知Sn是等差数列{an}的前n项和,且a3=-6,S5=S6.‎ ‎(1)求{an}的通项公式;‎ ‎(2)若等比数列{bn}满足b1=a2,b2=S3,求{bn}的前n项和.‎ ‎2.已知{an}是公差为3的等差数列,数列{bn}满足b1=1,b2=,anbn+1+bn+1=nbn.‎ ‎(1)求{an}的通项公式;‎ ‎(2)求{bn}的前n项和.‎ ‎3.(2018北京西城一模,文15)设等差数列{an}的公差不为0,a2=1,且a2,a3,a6成等比数列.‎ ‎(1)求{an}的通项公式;‎ 7‎ ‎(2)设数列{an}的前n项和为Sn,求使Sn>35成立的n的最小值.‎ ‎4.已知等比数列{an}的前n项和为Sn,a1=3,且3S1,2S2,S3成等差数列.‎ ‎(1)求数列{an}的通项公式;‎ ‎(2)设bn=log3an,求Tn=b1b2-b2b3+b3b4-b4b5+…+b2n-1b2n-b2nb2n+1.‎ ‎5.(2018北京顺义一模,文16)已知{an}是等差数列,{bn}是单调递增的等比数列,且a2=b2=3,b1+b3=10,b1b3=a5.‎ 7‎ ‎(1)求{an}的通项公式;‎ ‎(2)设cn=求数列{cn}的前n项和.‎ ‎6.设{an}是公比大于1的等比数列,Sn为数列{an}的前n项和,已知S3=7,且a1+3,‎3a2,a3+4构成等差数列.‎ ‎(1)求数列{an}的通项;‎ ‎(2)令bn=ln ,n=1,2,…,求数列{bn}的前n项和Tn.‎ ‎7.(2018山西吕梁一模,文17)已知{an}是首项为1的等比数列,数列{bn}满足b1=2,b2=5,且anbn+1=anbn+an+1.‎ ‎(1)求数列{an}的通项公式;‎ ‎(2)求数列{bn}的前n项和.‎ 7‎ ‎8.(2018天津卷,文18)设{an}是等差数列,其前n项和为Sn(n∈N*);{bn}是等比数列,公比大于0,其前n项和为Tn(n∈N*).已知b1=1,b3=b2+2,b4=a3+a5,b5=a4+‎2a6.‎ ‎(1)求Sn和Tn;‎ ‎(2)若Sn+(T1+T2+…+Tn)=an+4bn,求正整数n的值.‎ 参考答案 专题突破练12　等差、等比数列的 综合问题 ‎1.解 (1)设等差数列{an}的公差为d.‎ 因为S5=S6,所以a6=a3+3d=0.‎ 因为a3=-6,所以d=2,a1=-10.‎ 所以an=2n-12.‎ 7‎ ‎(2)设等比数列{bn}的公比为q.‎ 由(1)可知,b1=-8,b2=-24,‎ 所以q=3.‎ 数列{bn}的前n项和为=4(1-3n).‎ ‎2.解 (1)由已知,a1b2+b2=b1,b1=1,b2=,得a1=2.‎ 所以数列{an}是首项为2,公差为3的等差数列,通项公式为an=3n-1.‎ ‎(2)由(1)和anbn+1+bn+1=nbn得bn+1=,因此{bn}是首项为1,公比为的等比数列.记{bn}的前n项和为Sn,‎ 则Sn=.‎ ‎3.解 (1)设等差数列{an}的公差为d,d≠0.‎ ‎∵a2,a3,a6成等比数列,‎ ‎∴=a2·a6,‎ 即(1+d)2=1+4d,‎ 解得d=2或d=0(舍去d=0),‎ ‎∴an=a2+(n-2)d=2n-3.‎ ‎(2)∵an=2n-3,∴Sn==n2-2n.‎ 依题意有n2-2n>35,解得n>7.‎ 故使Sn>35成立的n的最小值为8.‎ ‎4.解 (1)∵3S1,2S2,S3成等差数列,‎ ‎∴4S2=3S1+S3,‎ ‎∴4(a1+a2)=‎3a1+(a1+a2+a3),‎ 即a3=‎3a2,∴公比q=3,‎ ‎∴an=a1qn-1=3n.‎ ‎(2)由(1)知,bn=log3an=log33n=n,‎ ‎∵b2n-1b2n-b2nb2n+1=(2n-1)·2n-2n(2n+1)=-4n,∴Tn=(b1b2-b2b3)+(b3b4-b4b5)+…+(b2n-1b2n-b2nb2n+1)=-4(1+2+…+n)=-4×=-2n2-2n.‎ ‎5.解 (1)设等差数列{an}的公差为d,等比数列{bn}的公比为q.‎ 7‎ 由 解得 由 解得 所以an=2n-1.‎ ‎(2)设数列{cn}的前n项和为Sn,‎ 由(1)可知an=2n-1,bn=b1qn-1=3n-1.‎ 当n≤5时,Sn=a1+a2+…+an==n2.‎ 当n>5时,Sn=a1+a2+…+a5+b6+b7+…+bn==25+.‎ ‎6.解 (1)由已知得 解得a2=2.‎ 设数列{an}的公比为q,‎ 由a2=2可得a1=,a3=2q.‎ 又S3=7,所以+2+2q=7,‎ 即2q2-5q+2=0.‎ 解得q=2或q=.‎ ‎∵q>1,∴q=2,∴a1=1.‎ 故数列{an}的通项为an=2n-1.‎ ‎(2)由(1)得=23n,‎ 7‎ ‎∴bn=ln 23n=3nln 2.‎ ‎∵bn+1-bn=3ln 2,‎ ‎∴数列{bn}为等差数列.‎ ‎∴Tn=b1+b2+…+bn=ln 2.‎ 故Tn=ln 2.‎ ‎7.解 (1)把n=1代入已知等式得a1b2=a1b1+a2,∴a2=a1b2-a1b1=‎3a1.‎ ‎∴{an}是首项为1,公比为3的等比数列,即an=3n-1.‎ ‎(2)由已知得bn+1-bn==3,‎ ‎∴{bn}是首项为2,公差为3的等差数列,其通项公式为bn=3n-1,‎ ‎∴Sn=.‎ ‎8.解 (1)设等比数列{bn}的公比为q.由b1=1,b3=b2+2,可得q2-q-2=0.因为q>0,可得q=2,故bn=2n-1.所以,Tn==2n-1.‎ 设等差数列{an}的公差为d.由b4=a3+a5,可得a1+3d=4.由b5=a4+‎2a6,可得‎3a1+13d=16,从而a1=1,d=1,故an=n.所以,Sn=.‎ ‎(2)由(1),有 T1+T2+…+Tn=(21+22+…+2n)-n=-n=2n+1-n-2.‎ 由Sn+(T1+T2+…+Tn)=an+4bn可得,+2n+1-n-2=n+2n+1,‎ 整理得n2-3n-4=0,解得n=-1(舍),或n=4.‎ 所以,n的值为4.‎ 7‎