2020届高考数学大二轮复习 第1部分第2讲 向量运算与复数运算、算法、推理与证明练习 10页

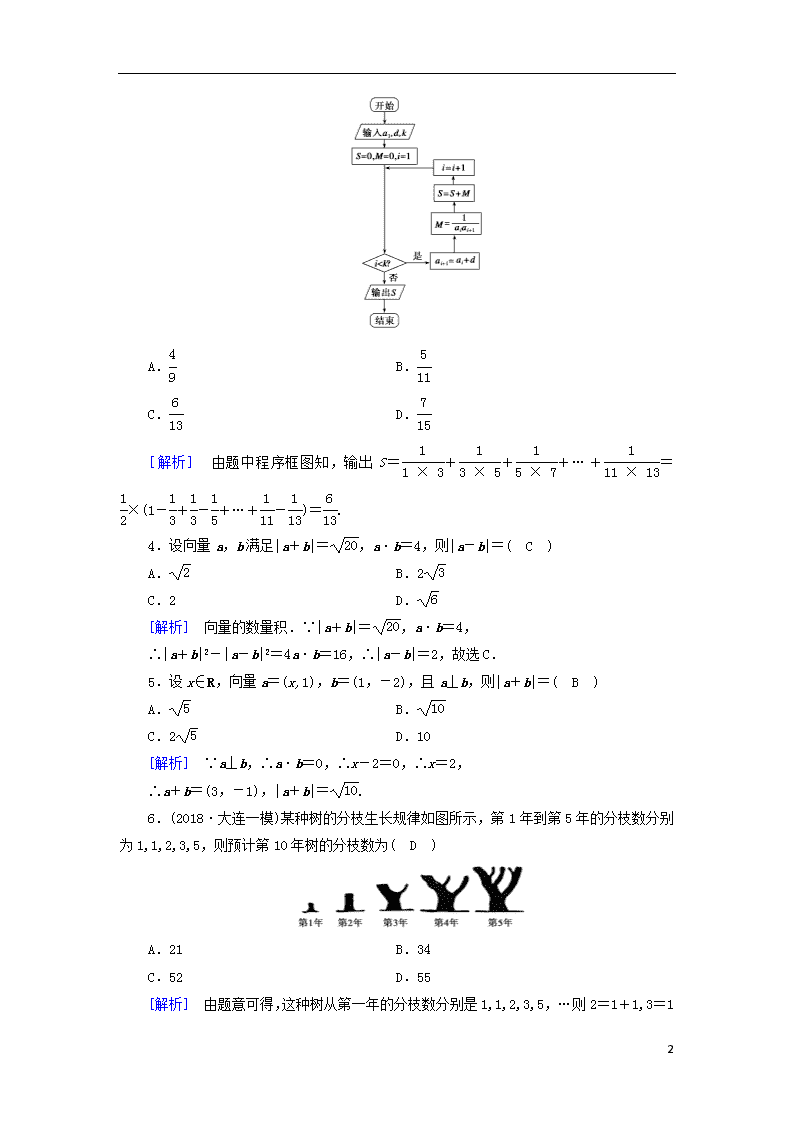
第一部分 专题一 第二讲 向量运算与复数运算、算法、推理与证明 A组 ‎1．(2017·全国卷Ⅱ，1)＝( D )‎ A．1＋2i　　 B．1－2i　　　‎ C．2＋i　　 D．2－i ‎[解析]　＝＝＝2－i.‎ 故选D．‎ ‎2．(文)已知i为虚数单位，则复数＝( C )‎ A．2＋i B．2－i ‎ C．－1－2i D．－1＋2i ‎[解析]　＝＝－1－2i，故选C．‎ ‎(理)若(1＋2ai)i＝1－bi，其中a、b∈R，则|a＋bi|＝( C )‎ A．＋i B． ‎ C． D． ‎[解析]　∵(1＋2ai)i＝－‎2a＋i＝1－bi，‎ ‎∴a＝－，b＝－1，‎ ‎∴|a＋bi|＝|－－i |＝＝.‎ ‎3．(2018·济南二模)已知数列{an}，观察如图所示的程序框图，若输入a1＝1，d＝2，k＝7，则输出的结果为( C )‎ 10‎ A． B． ‎ C． D． ‎[解析]　由题中程序框图知，输出S＝＋＋＋…＋＝×(1－＋－＋…＋－)＝.‎ ‎4．设向量a，b满足|a＋b|＝，a·b＝4，则|a－b|＝( C )‎ A． B．2 ‎ C．2 D． ‎[解析]　向量的数量积．∵|a＋b|＝，a·b＝4，‎ ‎∴|a＋b|2－|a－b|2＝‎4a·b＝16，∴|a－b|＝2，故选C．‎ ‎5．设x∈R，向量a＝(x,1)，b＝(1，－2)，且a⊥b，则|a＋b|＝( B )‎ A． B． ‎ C．2 D．10‎ ‎[解析]　∵a⊥b，∴a·b＝0，∴x－2＝0，∴x＝2，‎ ‎∴a＋b＝(3，－1)，|a＋b|＝.‎ ‎6．(2018·大连一模)某种树的分枝生长规律如图所示，第1年到第5年的分枝数分别为1,1,2,3,5，则预计第10年树的分枝数为( D )‎ A．21 B．34‎ C．52 D．55‎ ‎[解析]‎ 10‎ ‎　由题意可得，这种树从第一年的分枝数分别是1,1,2,3,5，…则2＝1＋1,3＝1＋2,5＝2＋3，即从第三项起，每一项都等于前两项的和，所以第10年树的分枝数是21＋34＝55.故选D．‎ ‎7．下面框图所给的程序运行结果为S＝28，那么判断框中应填入的关于k的条件是( D )‎ A．k＝8? B．k≤7?‎ C．k<7? D．k>7?‎ ‎[解析]　开始→k＝10，S＝1，满足条件→S＝1＋10＝11，k＝10－1＝9，满足条件→S＝11＋9＝20，k＝9－1＝8，满足条件→S＝20＋8＝28，k＝8－1＝7.由于输出S的值为28，故k＝7不再满足条件，故选D．‎ ‎8．设D，E，F分别为△ABC的三边BC、CA、AB的中点，则＋＝( A )‎ A． B． C． D． ‎[解析]　如图，‎ ＋ ‎＝－(＋)－(＋)‎ ‎＝－(＋)＝(＋)＝.‎ 选A．‎ ‎9．对任意向量a，b，下列关系式中不恒成立的是( B )‎ A．|a·b|≤|a||b|‎ B．|a－b|≤||a|－|b||‎ C．(a＋b)2＝|a＋b|2‎ D．(a＋b)·(a－b)＝a2－b2‎ ‎[解析]　由|a·b|＝||a|·|b|·cosθ|，‎ 因为－1≤cosθ≤1，所以|a·b|≤|a||b|恒成立；‎ 由向量减法的几何意义结合三角形的三边关系可得|a－b|≥||a|－|b||，故B选项不成立；‎ 10‎ 根据向量数量积的运算律C，D选项恒成立．‎ ‎10．36的所有正约数之和可按如下方法得到：因为36＝22×32，所以36的所有正约数之和为(1＋3＋32)＋(2＋2×3＋2×32)＋(22＋22×3＋22×32)＝(1＋2＋22)(1＋3＋32)＝91，参照上述方法，可求得200的所有正约数之和为( C )‎ A．201 B．‎411 C．465 D．565‎ ‎[解析]　200的所有正约数之和可按如下方法得到：因为200＝23×52，所以200的所有正约数之和为(1＋2＋22＋23)·(1＋5＋52)＝465，所以200的所有正约数之和为465.‎ ‎11．设a∈R，若复数(1＋i)(a＋i)在复平面内对应的点位于实轴上，则a＝－1.‎ ‎[解析]　(1＋i)(a＋i)＝(a－1)＋(a＋1)i，所以a＋1＝0，a＝－1.‎ ‎12．已知a＝(1,2)，b＝(－2，m)，若a∥b，则|‎2a＋3b|等于4.‎ ‎[解析]　由a∥b⇒m＋4＝0，解得m＝－4，故‎2a＋3b＝2(1,2)＋3(－2，－4)＝(－4，－8)，因此|‎2a＋3b|＝＝4.‎ ‎13．已知△ABC的面积为2，且B＝，则·＝4.‎ ‎[解析]　设△ABC的三角A，B，C的对边分别为a，b，c，‎ 则S＝acsinB＝ac＝2，即ac＝8，‎ ·＝||||·cos(π－B)＝cacos＝8×＝4.‎ ‎14．执行下边的程序框图，若输入的x的值为1，则输出的y的值为13.‎ ‎[解析]　第一次执行程序，满足条件x＜2，x＝1＋1＝2；第二次执行程序，不满足条件x＜2，y＝3×22＋1＝13，输出y＝13，结束．答案为13.‎ ‎15．(2018·聊城一模)观察等式：f()＋f()＝1；f()＋f()＋f()＝；f()＋f()＋f()＋f()＝2；f()＋f()＋f()＋f()＋f()＝；‎ ‎…‎ 由以上几个等式的规律可猜想f()＋f()＋f()＋…＋f()＝‎ 10‎ ‎1_009.‎ ‎[解析]　从所给四个等式看：等式右边依次为1，，2，，将其变为，，，，可以得到右边是一个分数，分母为2，分子与左边最后一项中自变量的分子相同，所以f()＋f()＋f()＋…＋f()＝＝1 009.‎ B组 ‎1．设复数z1＝1＋i，z2＝2＋bi，若为实数，则实数b等于( D )‎ A．－2 B．－‎1 C．1 D．2‎ ‎[解析]　＝＝ ‎＝，‎ 若其为实数，则有＝0，解得b＝2.‎ ‎2．(文)(2018·石景山检测)已知复数z＝(a2－1)＋(a＋1)i，若z是纯虚数，则实数a等于( B )‎ A．2 B．1 ‎ C．0 D．－1‎ ‎[解析]　∵z为纯虚数，∴∴a＝1.‎ ‎(理)已知复数z1＝1＋i，z2＝a＋i，若z1·z2为纯虚数，则实数a的值为( B )‎ A．－1 B．1 ‎ C．－2 D．2‎ ‎[解析]　∵z1·z2＝(a－1)＋(a＋1)i为纯虚数，‎ ‎∴，∴a＝1.‎ ‎3．(2017·全国卷Ⅱ，4)设非零向量a，b满足|a＋b|＝|a－b|，则( A )‎ A．a⊥b B．|a|＝|b| ‎ C．a∥b D．|a|>|b|‎ ‎[解析]　方法一：∵|a＋b|＝|a－b|，‎ ‎∴|a＋b|2＝|a－b|2.‎ ‎∴a2＋b2＋‎2a·b＝a2＋b2－‎2a·b.‎ ‎∴a·b＝0.‎ ‎∴a⊥b.‎ 故选A．‎ 方法二：利用向量加法的平行四边形法则．‎ 10‎ 在▱ABCD中，设＝a，＝b，‎ 由|a＋b|＝|a－b|知||＝||，∴|AC|＝|DB|‎ 从而四边形ABCD为矩形，即AB⊥AD，故a⊥b.‎ 故选A．‎ ‎4．执行如图所示的程序框图，若输入的a值为1，则输出的k值为( B )‎ A．1 B．2 ‎ C．3 D．4‎ ‎[解析]　输入a＝1，则b＝1，第一次循环，a＝＝－，k＝1；第二次循环，a＝＝－2，k＝2；第三次循环，a＝＝1，此时a＝b，结束循环，输出k＝2.故选B．‎ ‎5．(2018·潍坊一模)若复数z＝m(m－1)＋(m－1)(m－2)i是纯虚数，其中m是实数，i2＝－1，则等于( D )‎ A． B．－ ‎ C． D．－ ‎[解析]　因为复数z＝m(m－1)＋(m－1)·(m－2)i是纯虚数，所以m(m－1)＝0且(m－1)(m－2)≠0，所以m＝0，则＝＝－.‎ ‎6．设向量a，b满足|a|＝|b|＝|a＋b|＝1，则|a－tb|(t∈R)的最小值为( A )‎ 10‎ A． B． ‎ C．1 D．2‎ ‎[解析]　由于|a|＝|b|＝|a＋b|＝1，于是|a＋b|2＝1，即a2＋‎2a·b＋b2＝1，‎ 即a·b＝－.‎ ‎|a－tb|2＝a2－2ta·b＋t2b2＝(1＋t2)－2ta·b＝t2＋t＋1≥，故|a－tb|的最小值为.‎ ‎7．如图所示将若干个点摆成三角形图案，每条边(包括两个端点)有n(n>1，n∈N)个点，相应的图案中总的点数记为an，则＋＋＋…＋＝( C )‎ A． B． C． D． ‎[解析]　每条边有n个点，所以三条边有3n个点，三角形的3个顶点都被重复计算了一次，所以减3个顶点，即an＝3n－3，那么＝＝＝－，‎ 则＋＋＋…＋＝(－)＋(－)＋(－)＋…(－)＝1－＝.故选C．‎ ‎8．中国古代有计算多项式值的秦九韶算法，下图是实现该算法的程序框图．执行该程序框图，若输入的x＝2，n＝2，依次输入的a为2,2,5，则输出的s＝( C )‎ 10‎ A．7 B．12 ‎ C．17 D．34‎ ‎[解析]　由程序框图知，‎ 第一次循环：x＝2，n＝2，a＝2，s＝0×2＋2＝2，k＝1；‎ 第二次循环：a＝2，s＝2×2＋2＝6，k＝2；‎ 第三次循环：a＝5，s＝6×2＋5＝17，k＝3.结束循环，输出s的值为17，故选C．‎ ‎9．设复数z的共轭复数为，若z＝1－i(i为虚数单位)，则＋z2的虚部为－1.‎ ‎[解析]　∵z＝1－i(i为虚数单位)，‎ ‎∴＋z2＝＋(1－i)2＝－2i＝－2i＝－i，故其虚部为－1.‎ ‎10．(文)(2018·厦门联考)刘老师带甲、乙、丙、丁四名学生去西安参加自主招生考试，考试结束后刘老师向四名学生了解考试情况．四名学生回答如下：‎ 甲说：“我们四人都没考好．”‎ 乙说：“我们四人中有人考得好．”‎ 丙说：“乙和丁至少有一人没考好．”‎ 丁说：“我没考好．”‎ 结果，四名学生中有两人说对了，则这四名学生中的乙，丙两人说对了．‎ ‎[解析]　甲与乙的关系是对立事件，二人说话矛盾，必有一对一错，如果选丁正确，则丙也是对的，所以丁错误，可得丙正确，此时乙正确．故答案为乙，丙．‎ ‎(理)(2018·湖北七市联考)观察下列等式：‎ ‎1＋2＋3＋…＋n＝n(n＋1)；‎ ‎1＋3＋6＋…＋n(n＋1)＝n(n＋1)(n＋2)；‎ 10‎ ‎1＋4＋10＋…＋n(n＋1)(n＋2)＝n(n＋1)(n＋2)·(n＋3)；‎ ‎……‎ 可以推测，1＋5＋15＋…＋n(n＋1)(n＋2)(n＋3)＝n(n＋1)(n＋2)(n＋3)(n＋4)(n∈N*).‎ ‎[解析]　根据式子中的规律可知，等式右侧为n(n＋1)(n＋2)(n＋3)(n＋4)‎ ‎＝n(n＋1)(n＋2)(n＋3)(n＋4)(n∈N*)‎ ‎11．(2017·江苏卷，4)如图是一个算法流程图，若输入x的值为，则输出y的值是－2.‎ ‎[解析]　输入x＝<1，执行y＝2＋log2＝2－4＝－2，故输出y的值为－2.‎ ‎12．如图所示，A、B、C是圆O上的三点，线段CO的延长线 与线段BA的延长线交于圆O外的点D，若＝m＋n，则m＋n的取值范围是(－1,0).‎ ‎[解析]　根据题意知，线段CO的延长线与线段BA的延长线的交点为D，则＝t.‎ ‎∵D在圆外，∴t<－1，‎ 又D、A、B共线，∴存在λ、μ，使得＝λ＋μ，且λ＋μ＝1，又由已知，＝m＋n，‎ ‎∴tm＋tn＝λ＋μ，‎ 10‎ ‎∴m＋n＝，故m＋n∈(－1,0)．‎ 10‎