浙江高考数学文理不分试卷 14页

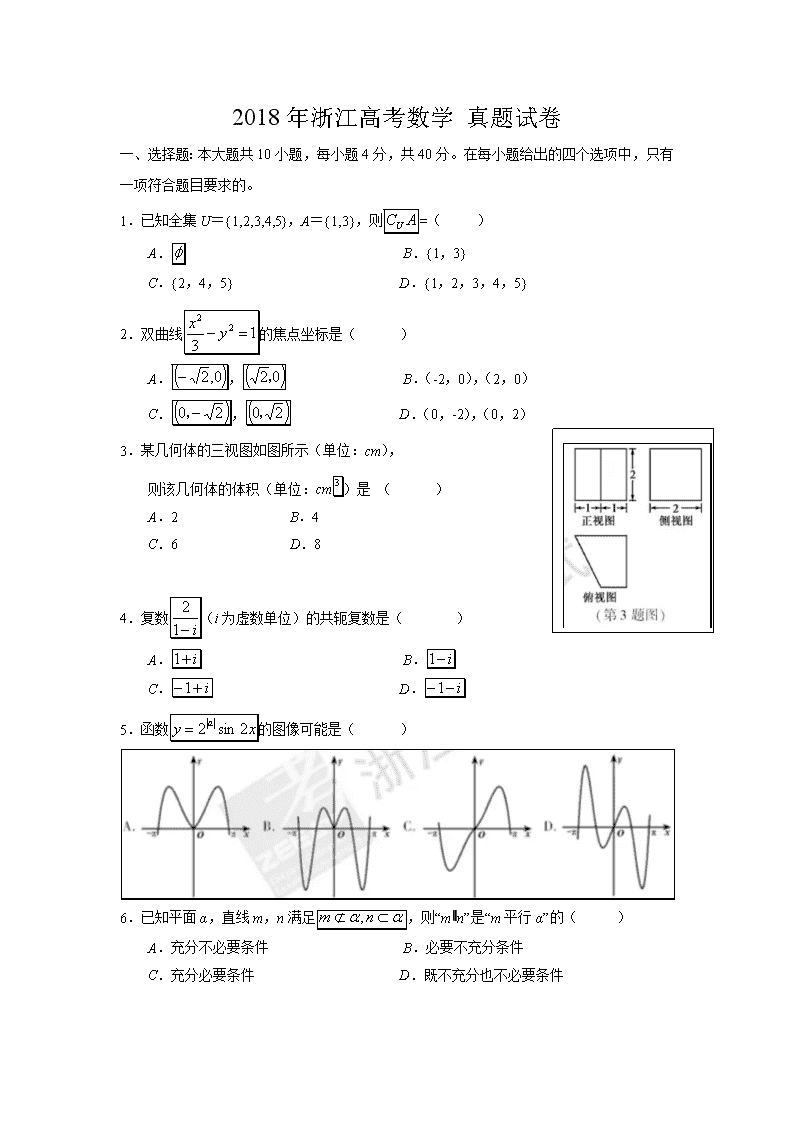
‎2018年浙江高考数学 真题试卷 一、 选择题：本大题共10小题，每小题4分，共40分。在每小题给出的四个选项中，只有一项符合题目要求的。‎ 1． 已知全集U＝{1,2,3,4,5}，A＝{1,3}，则=（ ）‎ A．　　　　　　　　 B．{1，3}‎ C．{2，4，5} D．{1，2，3，4，5}‎ ‎2．双曲线的焦点坐标是（ ）‎ A．，　　　　　　　 B．（-2，0），（2，0）‎ C．， D．（0，-2），（0，2）‎ ‎3．某几何体的三视图如图所示（单位：cm），‎ 则该几何体的体积（单位：cm）是 （ ）‎ A．2　　　　　　　　B．4‎ C．6 D．8‎ ‎ ‎ ‎4．复数（i为虚数单位）的共轭复数是（ ）‎ A．　　　　　　　　 B．‎ C． D．‎ ‎5．函数的图像可能是（ ）‎ ‎6．已知平面α，直线m，n满足，则“m∥n”是“m平行α”的（ ）‎ A．充分不必要条件　　　　　 B．必要不充分条件 C．充分必要条件 D．既不充分也不必要条件 ‎2018年浙江高考数学 真题试卷 一、 选择题：本大题共10小题，每小题4分，共40分。在每小题给出的四个选项中，只有一项符合题目要求的。‎ 1． 已知全集U＝{1,2,3,4,5}，A＝{1,3}，则=（ ）‎ A．　　　　　　　　 B．{1，3}‎ C．{2，4，5} D．{1，2，3，4，5}‎ ‎2．双曲线的焦点坐标是（ ）‎ A．，　　　　　　　 B．（-2，0），（2，0）‎ C．， D．（0，-2），（0，2）‎ ‎3．某几何体的三视图如图所示（单位：cm），‎ 则该几何体的体积（单位：cm）是 （ ）‎ A．2　　　　　　　　B．4‎ C．6 D．8‎ ‎ ‎ ‎4．复数（i为虚数单位）的共轭复数是（ ）‎ A．　　　　　　　　 B．‎ C． D．‎ ‎5．函数的图像可能是（ ）‎ ‎6．已知平面α，直线m，n满足，则“m∥n”是“m平行α”的（ ）‎ A．充分不必要条件　　　　　 B．必要不充分条件 C．充分必要条件 D．既不充分也不必要条件 ‎7．设01，则（ ）‎ A．<，<　　　 B．>，<‎ C．<，> D．>，>‎ 二、填空题：本大题共7小题，多空题6分，单空题每题4分，共36分。‎ ‎11．我国古代数据著作《张邱建算经》中记载百鸡问题：“今有鸡翁一，值钱五；鸡母一，值钱三；鸡雏三，值钱一。凡百钱，买鸡百只，间鸡翁、母、雏各几何？”设鸡翁，鸡母，鸡雏个数分别为x，y，z，则，当z=81时，x=______，y=_______.‎ ‎12．若x、y满足约束条件，则Z=x=3y的最小值是_______，最大值是________.‎ ‎13．在△ABC中，角A，B，C所对的边分别为a，b，c，若a=，b=2，A=60°，则sinB=______，c=_______.‎ ‎14．二项式的展开式的常数项是______ ___.‎ ‎15．已知，函数，当时，不等式<0的解集 是___________，若恰有2个零点，则的取值范围是_____________.‎ ‎16．从1，3，5，7，9中任取2个数字，从0，2，4，6中任取2个数字，一共可以 组成____个没有重复数字的四位数（用数字作答）‎ ‎17．已知一点P（0，1），椭圆（m>1）上两点A，B满足，‎ 则当m=_________，点B横坐标的绝对值最大。‎ 三、解答题：本大题共5小题，共74分。解答应写出文字说明、证明过程或验算步骤。‎ ‎18．（本题满分14分）已知角α的顶点与原点O重合，始边与x轴的非负半轴重合，它的终边过点P（，）。‎ ‎（1）求sin（）的值；‎ ‎（2）若角β满足sin（α+β）=，求cosβ的值。‎ ‎19．（本题满分15分）如图，已知多面体，AA，BB，CC均垂直于平面ABC，∠ABC=120°，AA=4，CC=1，AB=BC=BB=2.‎ ‎（1）证明：AB⊥平面 ‎（2）求直线AC与平面ABB所成角的正弦值。‎ ‎20.（本题满分15分）已知等比数列{an}的公比q>1，且，是，的等差中项，数列{}满足，数列的前n项和为。‎ （1） 求q的值；‎ （2） 求数列{}的通项公式。‎ ‎21.（本题满分15分）如图，已知点P是y轴左侧（不含y轴）一点，抛物线C：上存在不同的两点A、B满足PA、PB的终点均在C上。‎ （1） 设AB的终点为M，证明：PM垂直于y轴；‎ （2） 若P是半椭圆（x<0）上的动点，求△PAB面积的取值范围。‎ ‎22.（本题满分15分）已知函数 （1） 若在x=x，x（x≠x）处导数相等，证明：>8-8ln2;‎ （2） 若a≤3-4ln2，证明：对于任意k>0，直线y=kx+a与曲线有唯一公共点。‎