高考模拟考试数学试题及答案文 7页

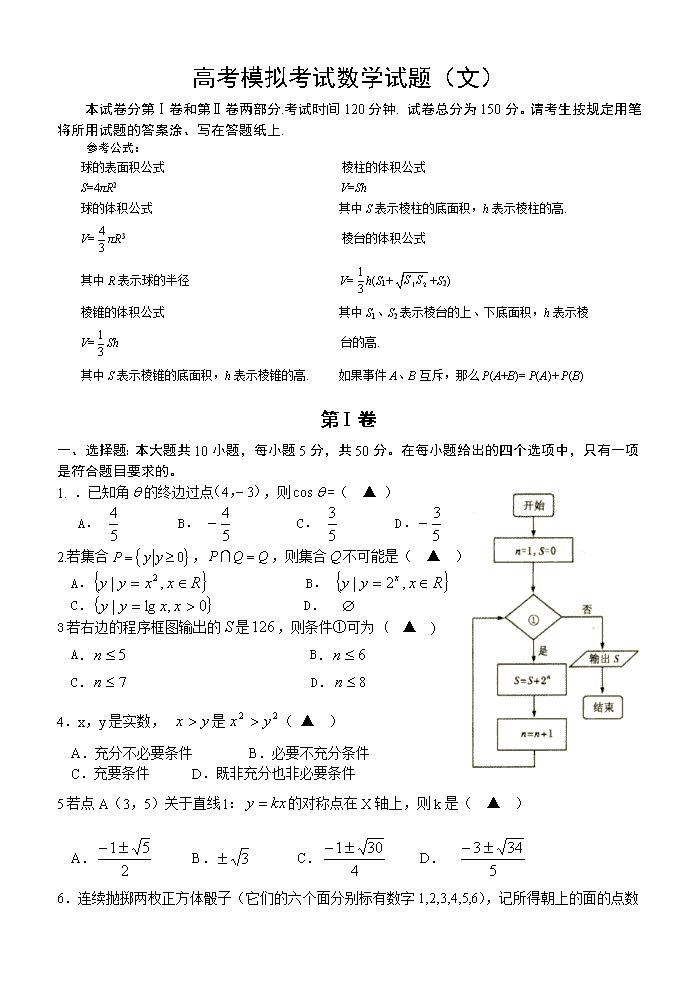
高考模拟考试数学试题（文）‎ 本试卷分第Ⅰ卷和第Ⅱ卷两部分.考试时间120分钟. 试卷总分为150分。请考生按规定用笔将所用试题的答案涂、写在答题纸上.‎ 参考公式：‎ 球的表面积公式 棱柱的体积公式 S=4πR2 V=Sh 球的体积公式 其中S表示棱柱的底面积，h表示棱柱的高.‎ V=πR3 棱台的体积公式 其中R表示球的半径 V=h(S1++S2)‎ 棱锥的体积公式 其中S1、S2表示棱台的上、下底面积，h表示棱 V=Sh 台的高.‎ 其中S表示棱锥的底面积，h表示棱锥的高. 如果事件A、B互斥，那么P(A+B)= P(A)+ P(B)‎ ‎ ‎ 第Ⅰ卷 一、选择题：本大题共10小题，每小题5分，共50分。在每小题给出的四个选项中，只有一项是符合题目要求的。‎ ‎1. ．已知角的终边过点，则=（　▲ ）‎ A． B． C． 　 D． ‎ ‎2.若集合，，则集合不可能是（　▲ ） ‎ A． 　　　B． ‎ C． 　　 　 D． ‎ ‎3若右边的程序框图输出的是，则条件①可为 (　▲ ) ‎ A． 　　　　 　　 B．‎ C． 　　　　　　D．‎ ‎4．x，y是实数， 是（ ▲ ）‎ A．充分不必要条件 　　B．必要不充分条件 ‎ C．充要条件 D．既非充分也非必要条件 ‎5若点A（3，5）关于直线l：的对称点在X轴上，则k是（ ▲ ）‎ A． 　 B． 　 C． 　 D． ‎ ‎6‎ ‎．连续抛掷两枚正方体骰子（它们的六个面分别标有数字1,2,3,4,5,6），记所得朝上的面的点数分别为x，y，过坐标原点和点P(x,y)的直线的倾斜角为θ，则θ＞60°的概率为　　（ ▲ ）‎ A． 　　　　 B． 　　 C． 　　　　　 D．‎ ‎7.函数有零点，则m的取值范围（ ▲ ）‎ A. B. C. 或 D. ‎ ‎8给定下列四个命题：‎ ‎①若一个平面内的两条直线与另一个平面都平行，则这两个平面平行；‎ ‎②若两个平面都垂直于同一条直线，则这两个平面平行；‎ ‎③若两个平面互相垂直，则在其中一个平面内的直线垂直另外一个平面； ‎ ‎④若两个平面互相平行，则在其中一个平面内的直线平行另外一个平面．‎ 其中为真命题的是 　　　　　（ ▲ ）‎ A．①和② B．②和③ 　 C．③和④ D．②和④‎ ‎9.已知点A（5，0）和⊙B：，P是⊙B上的动点，直线BP与线段AP的垂直平分线交于点Q，则点Q（x，y）所满足的轨迹方程为　　（ ▲ ）‎ A． B． C． D．‎ ‎10．已知曲线及两点和，其中.过，分别作轴的垂线，交曲线于，两点，直线与轴交于点，那么（ ▲　）‎ A．成等差数列 　B．成等比数列 ‎ C．成等差数列 　D．成等比数列 第Ⅱ卷 二、填空题：本大题有7小题,每小题4分,共28分。把答案填在答题卷的相应位置。‎ ‎11．设是虚数单位），则 　▲ 　‎ ‎12．过点P（1，2）的直线交圆于两点A、B，若点P是弦AB的中点，则弦AB所在直线的方程是　　▲ 　‎ ‎13．函数，若，则的所有可能值为　　▲ ‎ ‎14．已知实数满足不等式组,且的最小值为,则实数的值是　▲ ‎ ‎15．已知向量，，满足，且，，，则　▲ ． ‎ ‎16下图是一个几何体三视图，根据图中数据，计算该几何体的体积　▲ ‎ ‎17.已知ABCD是矩形，边长AB=3，BC=4，正方形ACEF边长为5，平面ACEF⊥平面ABCD，则多面体ABCDEF的外接球的表面积　▲ ‎ 三、解答题：本大题共5小题,满分72分.解答应写出文字说明,证明过程或演算步骤 ‎18.（本小题满分14分）‎ ‎ 在△ABC中，三内角A，B，C所对的边分别为a,b,c，且:‎ ‎(Ⅰ)求角A的大小； （Ⅱ）求的取值范围.‎ ‎19．（本小题满分14分）已知数列是一个公差大于0的等差数列，且满足,.‎ ‎(Ⅰ)求数列的通项公式； ‎ ‎（Ⅱ）若数列和数列满足等式：= ，求数列的前n项和.w.w.k.s..5.u.c.o.m ‎ ‎20.（本小题满分14分）如图, 是边长为的正方形，平面，，，与平面所成角为 A B C D F E ‎(Ⅰ)求证：平面；‎ ‎（Ⅱ）设点是线段上一个动点，试确定点 的位置，使得平面，并证明你的结论.‎ ‎21（本小题满分15分）已知函数且 ‎（Ⅰ）若在取得极小值－2，求函数的单调区间.‎ ‎（Ⅱ）令若的解集为A，且，求的取值范围.‎ ‎22（本小题满分15分）已知抛物线C：x=2py（p>0）上一点A（m，4）到其焦点的距离为.‎ ‎（I）求p和m的值；‎ ‎（Ⅱ）设B(-1,1),过点B任作两直线A1B1,A2B2,与抛物线C分别交于点A1,B1,A2,B2,过A1,B1的抛物线C的两切线交于P,过A2,B2的抛物线C的两切线交于Q,求PQ的直线方程.‎ 参考答案 一、选择题：‎ ACBDD,ADDCA 二、填空题：‎ ‎11, 1； 12， ； 13, 1或； 14， 6；‎ ‎15， ； 16， ； 17， ‎ 三，解答题：‎ ‎18.解：（1）‎ ‎………7分 ‎（2）（2），‎ 的取值范围………14分 ‎19.解：（1）‎ ‎ （2）= ‎ ‎ = ‎ ‎ 相减得-==2 ‎ ‎ 又 ‎ ‎ ‎ ‎ ‎ ‎ 故 ‎20.（1）∵平面， ∴DE⊥AC 在正方形ABCD中，AC⊥BD ‎∴平面 ‎(2) ‎ ‎21，解：（Ⅰ），依题意得 ‎ 解之，得： ‎ ‎ ∴ ………5分 由得：x＜－1或x＞1，由得：－1＜x＜1‎ ‎∴F(x)的增区间为（－∞，－1），（1，+∞），减区间为（－1,1）………7分 ‎（Ⅱ）由得：2b＝a＋c, ‎ ‎ 从而， 由得： ………10分 ‎ 当a＞0时，；当a＜0时，‎ ‎ 而 得 ∴‎ ‎ 故的取值范围为（―3，―1） ………15分 ‎22，解：（Ⅰ）由抛物线方程得其准线方程：，根据抛物线定义 点到焦点的距离等于它到准线的距离，即，解得 抛物线方程为：，将代入抛物线方程，解得………6分 ‎（Ⅱ）因为点B(-1,1) 在抛物线C上，所以B1，B2即为点B，则过A1,B1的抛物线C的两切线交于P在过B的抛物线C的切线上,过A2,B2的抛物线C的两切线交于Q同样在过B的 抛物线C的切线上，故直线PQ就是抛物线C在点B(-1,1)处的切线，易求其直线方程为y＝―2x―1 ………15分