09高考立体几何题 4页

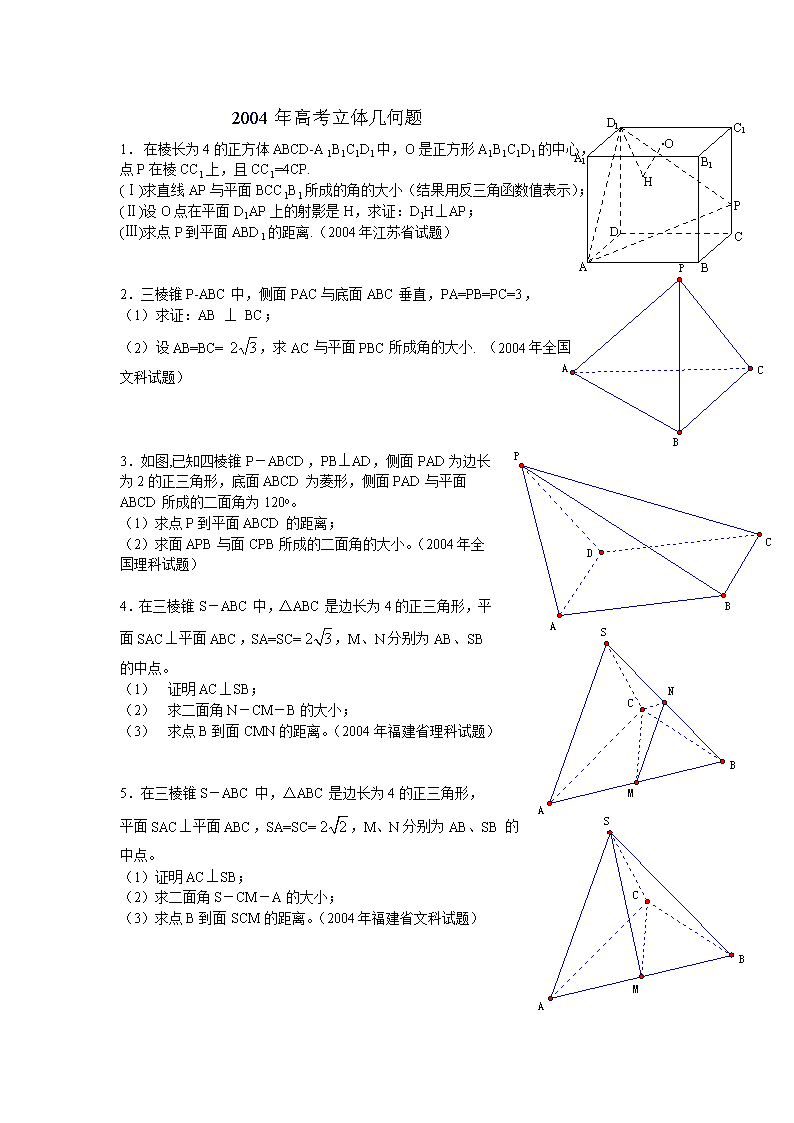
‎·‎ B1‎ P A C D A1‎ C1‎ D1‎ B O H ‎·‎ ‎2004年高考立体几何题 1． 在棱长为4的正方体ABCD-A1B‎1C1D1中，O是正方形A1B‎1C1D1的中心，‎ 点P在棱CC1上，且CC1=4CP.‎ ‎(Ⅰ)求直线AP与平面BCC1B1所成的角的大小（结果用反三角函数值表示）；‎ ‎(Ⅱ)设O点在平面D1AP上的射影是H，求证：D1H⊥AP；‎ ‎(Ⅲ)求点P到平面ABD1的距离.（2004年江苏省试题）‎ ‎2．三棱锥P-ABC中，侧面PAC与底面ABC垂直，PA=PB=PC=3，‎ （1） 求证：AB ⊥ BC；‎ （2） 设AB=BC=，求AC与平面PBC所成角的大小. （2004年全国文科试题）‎ ‎3．如图,已知四棱锥P－ABCD，PB⊥AD，侧面PAD为边长为2的正三角形，底面ABCD为菱形，侧面PAD与平面ABCD所成的二面角为120o。‎ ‎（1）求点P到平面ABCD的距离；‎ ‎（2）求面APB与面CPB所成的二面角的大小。（2004年全国理科试题）‎ ‎4．在三棱锥S－ABC中，△ABC是边长为4的正三角形，平面SAC⊥平面ABC，SA=SC=，M、N分别为AB、SB的中点。‎ （1） 证明AC⊥SB；‎ （2） 求二面角N－CM－B的大小；‎ （3） 求点B到面CMN的距离。（2004年福建省理科试题）‎ ‎5．在三棱锥S－ABC中，△ABC是边长为4的正三角形，‎ 平面SAC⊥平面ABC，SA=SC=，M、N分别为AB、SB 的中点。‎ ‎（1）证明AC⊥SB；‎ ‎（2）求二面角S－CM－A的大小；‎ ‎（3）求点B到面SCM的距离。（2004年福建省文科试题）‎ ‎6．如图，已知正方形ABCD和矩形ACEF所在平面互相垂直，‎ AB=，AF=1，M是线段EF的中点。‎ （1） 求证：AM∥平面BDE；‎ （2） 求证：AM⊥平面BDF；‎ （3） 求二面角A－DF－B的大小；（2004年浙江试题）‎ ‎7．如图，在棱长为1的正方体ABCD－A1B‎1C1D1中，E 是棱BC的中点，点F是棱CD上的动点。‎ （1） 试确定点F的位置，使得D1E⊥平面AB‎1F；‎ （2） 当D1E⊥平面AB‎1F时，求二面角C1―EF―A的大小。（2004年湖北省试题）‎ ‎8．如图，在底面是菱形的四棱锥P－ABCD中，∠ABC=60o，PA=AC=a，PB=PD=a，‎ 点E在PD上，且PE:ED=2:1。‎ （1） 证明：PA⊥平面ABCD；‎ ‎（2）求以AC为棱，EAC与DAC为面的二面角θ的大小；‎ ‎（3）在棱PC上是否存在点F，使BF∥平面EAC,并证明你的结论.（2004年湖南省试题）‎ ‎9．如图，在四棱锥P—ABCD中底面ABCD是正方形，侧棱PD⊥底面ABCD，PD=PC,EC是PC中点，作EF⊥PB于点F ‎（1）证明PA∥平面EDB；‎ （2） 证明PB⊥平面EFD；‎ （3） 求二面角C－PB－D的大小。（2004年天津市理科试题）‎ ‎10．如图，P－ABC是底面边长为1的正三棱锥，D、E、F分别是棱PA、PB、PC上的点，截面DEF∥底面ABC，且棱台DEF－ABC与棱锥P－ABC的棱长和相等（棱长和是指多面体中所有棱长之和）‎ （1） 证明P－ABC是正四面体；‎ （2） 设PD=PA，求二面角D－BC－A的大小；‎ （3） 设棱台DEF－ABC的体积为V，是否存在体积为V，且各条棱长均相等的平行六面体，使得它与棱台DEF－ABC有相同的棱长和？若存在，请具体构造出这样的一个平行六面体，并给出证明；若不存在，请说明理由。（2004年上海市高考题）‎ ‎11．如图，在正三棱柱ABC－A1B‎1C1中，AB=3，AA1=4，M为棱AA1的中点，P是BC上的一点，且由P沿棱柱侧面经过棱CC1到M的最短路线为，设这条最短路线与CC1的交点为N，求 ‎（I）该三棱柱的侧面展开图的对角线长；‎ ‎（II）PC和NC的长；‎ ‎（III）平面NMP与平面ABC所成二面角（锐角）的大小。（用反三角函数表示）‎ ‎（2004年北京市高考题）‎ ‎12．如图，四棱锥P－ABCD的底面是正方形，PA⊥底面ABCD，AE⊥PD，EF∥CD，AM=EF。‎ ‎（I）证明MF是异面直线与的公垂线；‎ ‎（II）若PA=3AB，求直线AC与平面EAM所成角的正弦值。（2004年重庆市高考题）‎ ‎13．如右下图,在长方体ABCD—A1B‎1C1D1中,已知AB= 4, AD =3, AA1= 2. E、F分别是线段AB、BC上的点，且EB= FB=1.‎ ‎(1) 求二面角C—DE—C1的正切值;‎ ‎(2) 求直线EC1与FD1所成的余弦值.（2004年广东省数学高考试题）‎ ‎14．如图，在棱长为1的正方体ABCD—A1B‎1C1D1中，AC与BD交于点E，C1B于BC1交于点F。‎ ‎（1）求证：AC1⊥平面BDC1；‎ ‎（2）求二面角的大小。（结果用反三角函数值表示）‎ ‎（2004年湖北省文科试题）‎