北京市顺义区高考数学二模试卷文科解析版 22页

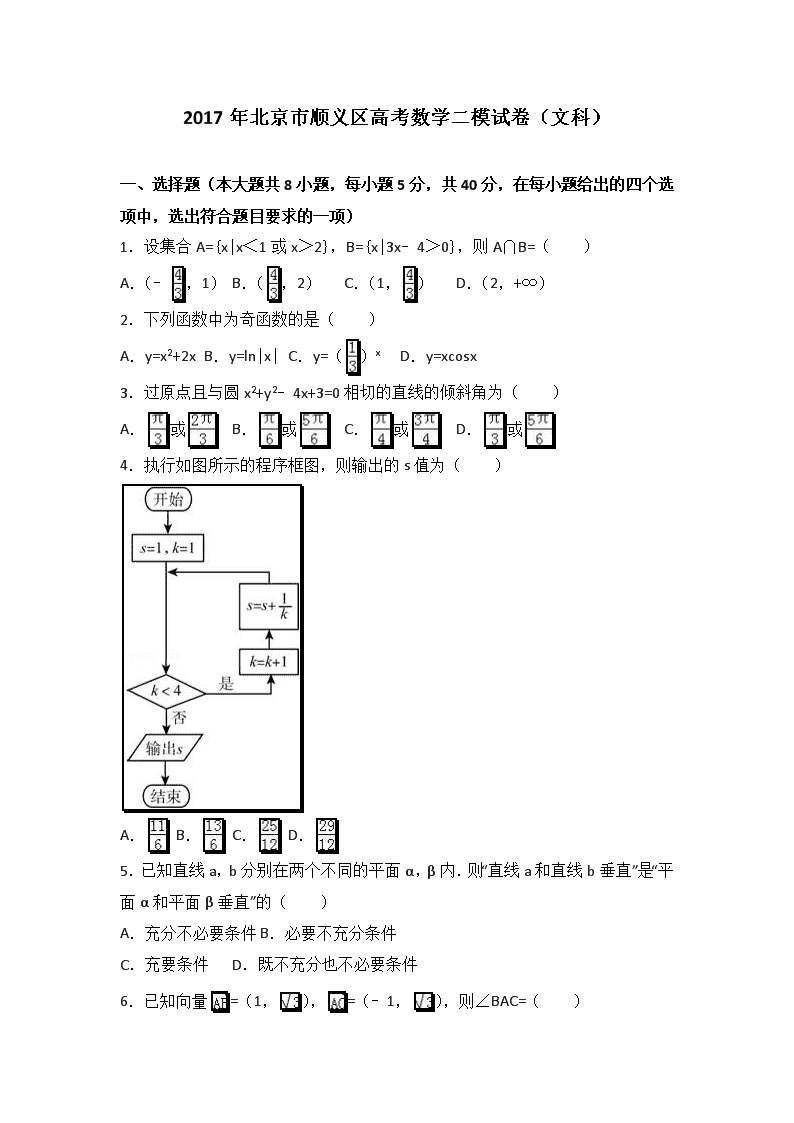
‎2017年北京市顺义区高考数学二模试卷（文科）‎ ‎　‎ 一、选择题（本大题共8小题，每小题5分，共40分，在每小题给出的四个选项中，选出符合题目要求的一项）‎ ‎1．设集合A={x|x＜1或x＞2}，B={x|3x﹣4＞0}，则A∩B=（　　）‎ A．（﹣，1） B．（，2） C．（1，） D．（2，+∞）‎ ‎2．下列函数中为奇函数的是（　　）‎ A．y=x2+2x B．y=ln|x| C．y=（）x D．y=xcosx ‎3．过原点且与圆x2+y2﹣4x+3=0相切的直线的倾斜角为（　　）‎ A．或 B．或 C．或 D．或 ‎4．执行如图所示的程序框图，则输出的s值为（　　）‎ A． B． C． D．‎ ‎5．已知直线a，b分别在两个不同的平面α，β内．则“直线a和直线b垂直”是“平面α和平面β垂直”的（　　）‎ A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 ‎6．已知向量=（1，），=（﹣1，），则∠BAC=（　　）‎ A．30° B．45° C．60° D．120°‎ ‎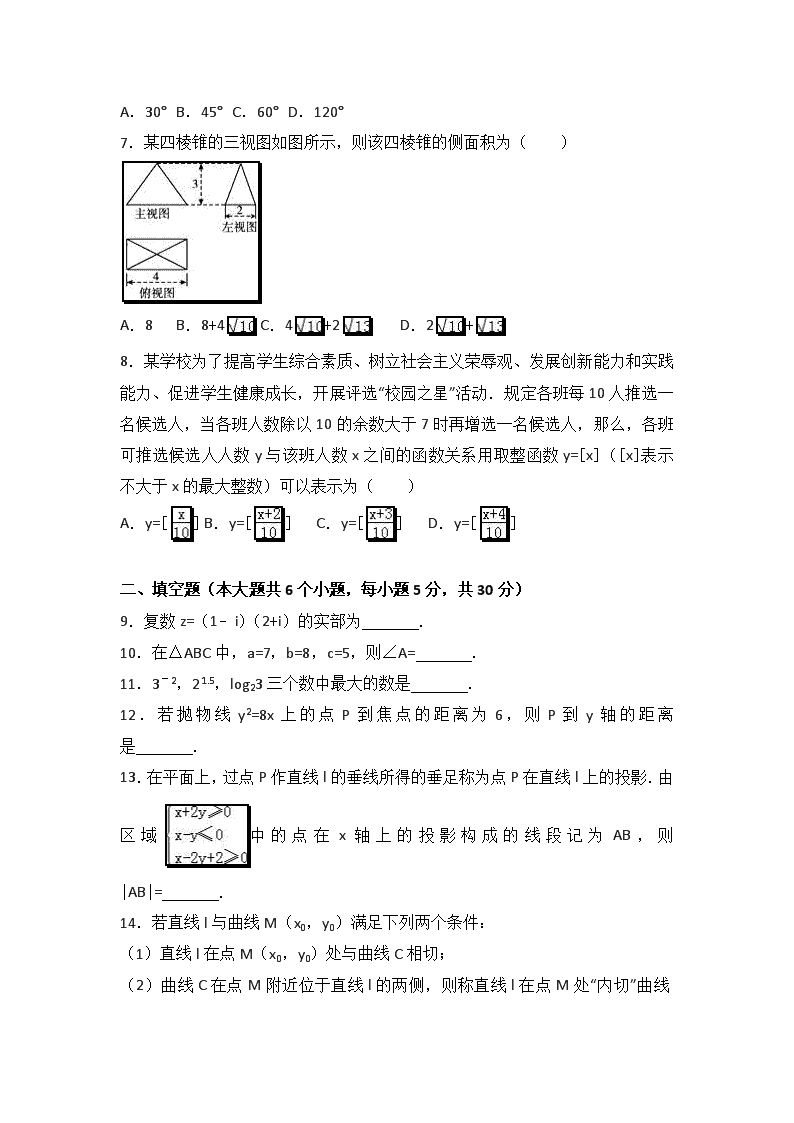7．某四棱锥的三视图如图所示，则该四棱锥的侧面积为（　　）‎ A．8 B．8+4 C．4+2 D．2+‎ ‎8．某学校为了提高学生综合素质、树立社会主义荣辱观、发展创新能力和实践能力、促进学生健康成长，开展评选“校园之星”活动．规定各班每10人推选一名候选人，当各班人数除以10的余数大于7时再增选一名候选人，那么，各班可推选候选人人数y与该班人数x之间的函数关系用取整函数y=[x]（[x]表示不大于x的最大整数）可以表示为（　　）‎ A．y=[] B．y=[] C．y=[] D．y=[]‎ ‎　‎ 二、填空题（本大题共6个小题，每小题5分，共30分）‎ ‎9．复数z=（1﹣i）（2+i）的实部为　 　．‎ ‎10．在△ABC中，a=7，b=8，c=5，则∠A=　 　．‎ ‎11．3﹣2，21.5，log23三个数中最大的数是　 　．‎ ‎12．若抛物线y2=8x上的点P到焦点的距离为6，则P到y轴的距离是　 　．‎ ‎13．在平面上，过点P作直线l的垂线所得的垂足称为点P在直线l上的投影．由区域中的点在x轴上的投影构成的线段记为AB，则|AB|=　 　．‎ ‎14．若直线l与曲线M（x0，y0）满足下列两个条件：‎ ‎（1）直线l在点M（x0，y0）处与曲线C相切；‎ ‎（2）曲线C在点M附近位于直线l的两侧，则称直线l在点M处“内切”曲线C．‎ 下列命题正确的是　 　（写出所有正确命题的编号）‎ ‎①直线l：y=0在点M（0，0）处“内切”曲线C：y=x3‎ ‎②直线l：y=x在点M（0，0）处“内切”曲线C：y=sinx ‎③直线l：y=x﹣1在点M（1，0）处“内切”曲线C：y=lnx．‎ ‎　‎ 三、解答题（本大题共6小题，共80分.解答应写出文字说明，证明过程或演算步骤）‎ ‎15．已知函数f（x）=sinxcosx+cos（π﹣x）cosx ‎（Ⅰ）求f（x）的最小正周期；‎ ‎（Ⅱ）求f（x）在区间[0，]上的最大值和最小值．‎ ‎16．已知数列{an}满足：a1=1，an+1=2an，数列{bn}满足：b1=3，b4=11，且{an+bn}为等差数列．‎ ‎（I） 求数列{an}和{bn}的通项公式；‎ ‎（II） 求数列{bn}的前n项和．‎ ‎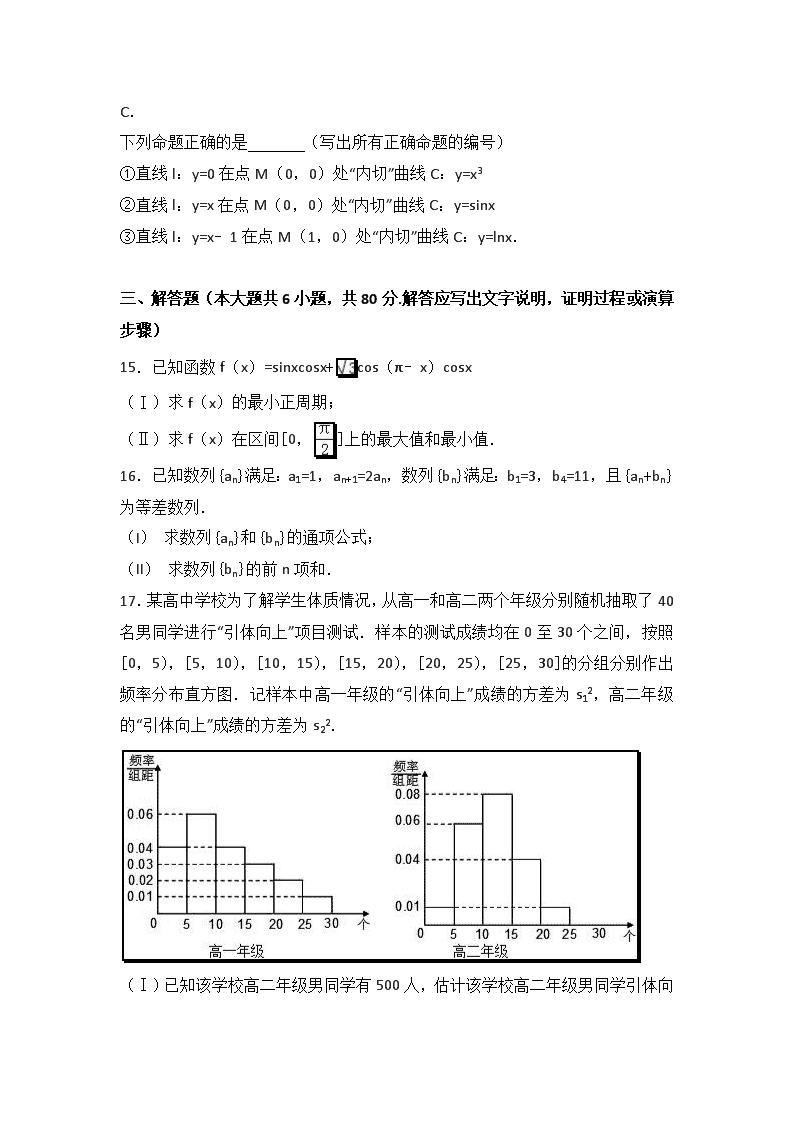17．某高中学校为了解学生体质情况，从高一和高二两个年级分别随机抽取了40名男同学进行“引体向上”项目测试．样本的测试成绩均在0至30个之间，按照[0，5），[5，10），[10，15），[15，20），[20，25），[25，30]的分组分别作出频率分布直方图．记样本中高一年级的“引体向上”成绩的方差为s12，高二年级的“引体向上”成绩的方差为s22．‎ ‎（Ⅰ）已知该学校高二年级男同学有500人，估计该学校高二年级男同学引体向上成绩不少于10个的人数；‎ ‎（Ⅱ）从样本中高一年级的成绩不小于20个男同学中随机抽取2人，求至少有1人成绩在[25，30]中的概率．‎ ‎（Ⅲ）比较s12与s22的大小（只需写出结果）．‎ ‎18．如图，正三角形ABE与菱形ABCD所在的平面互相垂直，AB=2，∠ABC=60°，M是AB的中点，N是CE的中点．‎ ‎（I）求证：EM⊥AD；‎ ‎（II）求证：MN∥平面ADE；‎ ‎（III）求点A到平面BCE的距离．‎ ‎19．已知函数f（x）=1+lnx﹣aex ‎（Ⅰ）若曲线y=f（x）在x=1处的切线与x轴平行，求实数a的值；‎ ‎（Ⅱ）若对任意x∈（0，+∞），不等式f（x）≤0恒成立，求实数a的取值范围．‎ ‎20．已知椭圆C： +=1（a＞b＞0）经过点（1，），离心率e=．‎ ‎（Ⅰ）求椭圆C的方程，‎ ‎（Ⅱ）设动直线l：y=kx+m与椭圆C相切，切点为T，且直线l与直线x=4相交于点S．试问：在坐标平面内是否存在一定点，使得以ST为直径的圆恒过该定点？若存在，求出该点的坐标；若不存在，请说明理由．‎ ‎　‎ ‎2017年北京市顺义区高考数学二模试卷（文科）‎ 参考答案与试题解析 ‎　‎ 一、选择题（本大题共8小题，每小题5分，共40分，在每小题给出的四个选项中，选出符合题目要求的一项）‎ ‎1．设集合A={x|x＜1或x＞2}，B={x|3x﹣4＞0}，则A∩B=（　　）‎ A．（﹣，1） B．（，2） C．（1，） D．（2，+∞）‎ ‎【考点】1E：交集及其运算．‎ ‎【分析】根据集合交集的定义进行求解即可．‎ ‎【解答】解：B={x|3x﹣4＞0}={x|x＞}，‎ 则A∩B={x|x＞2}，‎ 故选：D ‎　‎ ‎2．下列函数中为奇函数的是（　　）‎ A．y=x2+2x B．y=ln|x| C．y=（）x D．y=xcosx ‎【考点】3K：函数奇偶性的判断．‎ ‎【分析】直接利用基本函数的奇偶性判断选项即可．‎ ‎【解答】解：A．函数y=x2+2x为非奇非偶函数，故本选项错误；‎ B．函数y=ln|x|定义域不关于原点对称，非奇非偶函数，故本选项错误；‎ C．函数y=（）x不满足f（﹣x）=﹣f（x）不是奇函数，故本选项错误；‎ D．f（﹣x）=﹣xcos（﹣x）=﹣xcosx=﹣f（x），则f（x）为奇函数，故本选项正确；‎ 故选：D．‎ ‎　‎ ‎3．过原点且与圆x2+y2﹣4x+3=0相切的直线的倾斜角为（　　）‎ A．或 B．或 C．或 D．或 ‎【考点】I2：直线的倾斜角．‎ ‎【分析】由已知圆的方程求出圆心坐标和圆的半径，设出直线l的方程，由圆心到l的距离等于半径求得斜率，则直线l的倾斜角可求．‎ ‎【解答】解：由x2+y2﹣4x+3=0，得（x﹣2）2+y2=1，‎ ‎∴圆的圆心为（2，0），半径为1，‎ 设直线l的方程为kx﹣y=0，‎ 由圆与直线相切得： =1，‎ 解得k=．‎ 设直线l的倾斜角为θ（0≤θ＜π），‎ 由tanθ=±，得θ=或．‎ ‎∴直线l的倾斜角为或．‎ 故选：B．‎ ‎　‎ ‎4．执行如图所示的程序框图，则输出的s值为（　　）‎ A． B． C． D．‎ ‎【考点】EF：程序框图．‎ ‎【分析】模拟执行程序框图，依次写出每次循环得到的s，k的值，当k=4时不满足条件k＜4，退出循环，输出S的值即可得解．‎ ‎【解答】解：模拟执行程序框图，可得 s=1，k=1‎ 满足条件k＜4，执行循环体，k=2，s=1+‎ 满足条件k＜4，执行循环体，k=3，s=1++‎ 满足条件k＜4，执行循环体，k=4，s=1+++‎ 不满足条件k＜4，退出循环，输出s的值为s=1+++=．‎ 故选：C．‎ ‎　‎ ‎5．已知直线a，b分别在两个不同的平面α，β内．则“直线a和直线b垂直”是“平面α和平面β垂直”的（　　）‎ A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 ‎【考点】2L：必要条件、充分条件与充要条件的判断．‎ ‎【分析】根据直线垂直和面面垂直的判定条件分别进行判断即可．‎ ‎【解答】解：当a⊥b时，满足条件，但此时α∥β，即充分性不成立，‎ 当平面α和平面β垂直时，直线a和b平行，则直线a和直线b垂直不一定成立，‎ 故必要性不成立，‎ 则“直线a和直线b垂直”是“平面α和平面β垂直”‎ 的既不充分也不必要条件，‎ 故选：D ‎　‎ ‎6．已知向量=（1，），=（﹣1，），则∠BAC=（　　）‎ A．30° B．45° C．60° D．120°‎ ‎【考点】9R：平面向量数量积的运算．‎ ‎【分析】方法一：判断△ABC为等边三角形，问题得以解决，‎ 方法二：根据向量的夹角公式计算即可 ‎【解答】解：方法一：∵ =（1，），=（﹣1，），‎ ‎∴||=2，||=2， =﹣=（﹣2，0），‎ ‎∴||=2，‎ ‎∴△ABC为等边三角形，‎ ‎∴∠BAC=60°，‎ 方法二：：∵ =（1，），=（﹣1，），‎ ‎∴||=2，||=2， •=1×（﹣1）+×=2，‎ ‎∴cos∠BAC==，‎ ‎∵0°≤∠BAC≤180°，‎ ‎∴∠BAC=60°，‎ 故选：C．‎ ‎　‎ ‎7．某四棱锥的三视图如图所示，则该四棱锥的侧面积为（　　）‎ A．8 B．8+4 C．4+2 D．2+‎ ‎【考点】L!：由三视图求面积、体积．‎ ‎【分析】首先由三视图还原几何体，根据图中数据计算侧面斜高，进一步计算侧面积．‎ ‎【解答】解：由三视图得到几何体的直观图如图：四棱锥P﹣ABCD，其中OP=3，AB=CD=4，AD=BC=2，‎ 所以PE=，PF=，‎ 所以侧面积为2（S△PAB+S△PBC）=；‎ 故选：C．‎ ‎　‎ ‎8．某学校为了提高学生综合素质、树立社会主义荣辱观、发展创新能力和实践能力、促进学生健康成长，开展评选“校园之星”活动．规定各班每10人推选一名候选人，当各班人数除以10的余数大于7时再增选一名候选人，那么，各班可推选候选人人数y与该班人数x之间的函数关系用取整函数y=[x]（[x]表示不大于x的最大整数）可以表示为（　　）‎ A．y=[] B．y=[] C．y=[] D．y=[]‎ ‎【考点】36：函数解析式的求解及常用方法．‎ ‎【分析】由题意，根据规定10推选一名代表，当各班人数除以10的余数大于7时再增加一名代表，即余数分别为8，9时可以增选一名代表，也就是x要进一位，所以最小应该加2．进而得到解析式．‎ ‎【解答】由题意，根据规定10推选一名代表，当各班人数除以10的余数大于7时再增加一名代表，即余数分别为8，9时可以增选一名代表，也就是x要进一位，所以最小应该加2．因此利用取整函数可表示为y=[]；‎ 故选B．‎ ‎　‎ 二、填空题（本大题共6个小题，每小题5分，共30分）‎ ‎9．复数z=（1﹣i）（2+i）的实部为　3　．‎ ‎【考点】A2：复数的基本概念．‎ ‎【分析】直接把两个复数采用多项式乘多项式运算即可．‎ ‎【解答】解：z=（1一i）（2+i）=1×2+i﹣2i﹣i2=3﹣i，‎ 所以复数z的实部是3．‎ 故答案为3．‎ ‎　‎ ‎10．在△ABC中，a=7，b=8，c=5，则∠A=　　．‎ ‎【考点】HR：余弦定理．‎ ‎【分析】由已知利用余弦定理可求cosA的值，结合A的范围即可得解．‎ ‎【解答】解：∵a=7，b=8，c=5，‎ ‎∴cosA===，‎ ‎∴由A∈（0，π），可得A=．‎ 故答案为：．‎ ‎　‎ ‎11．3﹣2，21.5，log23三个数中最大的数是　21.5　．‎ ‎【考点】4M：对数值大小的比较．‎ ‎【分析】由于3﹣2=，21.5＞2，log23＜2，即可判断 ‎【解答】解：3﹣2=，21.5＞2，log23＜2，‎ ‎∴3﹣2，21.5，log23三个数中最大的数是21.5，‎ 故答案为：21.5‎ ‎　‎ ‎12．若抛物线y2=8x上的点P到焦点的距离为6，则P到y轴的距离是　4　．‎ ‎【考点】K8：抛物线的简单性质．‎ ‎【分析】根据抛物线的焦半径公式，求得x+=6，即可求得x的值，求得P到y轴的距离．‎ ‎【解答】解：∵抛物线y2=8x，则p=4，则焦点F（2，0），设P（x，y）‎ 由抛物线定义可知，抛物线上任一点到焦点的距离与到准线的距离是相等的，‎ ‎∴|MF|=6=x+2=6，‎ ‎∴x=4，‎ P到y轴的距离4，‎ 故答案为：4．‎ ‎　‎ ‎13．在平面上，过点P作直线l的垂线所得的垂足称为点P在直线l上的投影．由区域中的点在x轴上的投影构成的线段记为AB，则|AB|=　3　．‎ ‎【考点】7C：简单线性规划．‎ ‎【分析】作出不等式组对应的平面区域，利用投影的定义，利用数形结合进行求解即可．‎ ‎【解答】解：作出不等式组对应的平面区域如图：（阴影部分），‎ 区域内的点在直线x+y﹣2=0上的投影构成线段A′B′，‎ 由得A（﹣1，）‎ 由得B（2，﹣2），‎ 则|AB|=|2+1|=3，‎ 故答案为：3．‎ ‎　‎ ‎14．若直线l与曲线M（x0，y0）满足下列两个条件：‎ ‎（1）直线l在点M（x0，y0）处与曲线C相切；‎ ‎（2）曲线C在点M附近位于直线l的两侧，则称直线l在点M处“内切”曲线C．‎ 下列命题正确的是　①②　（写出所有正确命题的编号）‎ ‎①直线l：y=0在点M（0，0）处“内切”曲线C：y=x3‎ ‎②直线l：y=x在点M（0，0）处“内切”曲线C：y=sinx ‎③直线l：y=x﹣1在点M（1，0）处“内切”曲线C：y=lnx．‎ ‎【考点】6H：利用导数研究曲线上某点切线方程．‎ ‎【分析】分别求出每一个命题中曲线C的导数，得到曲线在点M处的导数值，求出曲线在点M处的切线方程，再由曲线在点M两侧的函数值与对应直线上点的值的大小判断是否满足条件（2），则正确的选项可求．‎ ‎【解答】解：①，由y=x3，得y′=3x2，则y′|x=0=0，直线y=0是在点M（0，0）处的曲线C的切线，‎ 又当x＞0时y＞0，当x＜0时y＜0，满足曲线C在M（0，0）附近位于直线y=0两侧，故命题①正确；‎ ‎②，由y=sinx，得y′=cosx，则y′|x=0=1，直线y=x是在点M（0，0）处的曲线的切线，‎ 满足曲线C在M（0，0）附近位于直线y=x两侧，故命题②正确；‎ ‎③，由y=lnx，得y′=，则y′|x=1=1，曲线在M（1，0）处的切线为y=x﹣1，‎ 由g（x）=x﹣1﹣lnx，得g′（x）=1﹣，当x∈（0，1）时，g′（x）＜0，当x∈（1，+∞）时，‎ g′（x）＞0．则g（x）在（0，+∞）上有极小值也是最小值，为g（1）=0．‎ 即y=x﹣1恒在y=lnx的上方，不满足曲线C在点M附近位于直线l的两侧，故命题③错误．‎ 故答案为：①②．‎ ‎　‎ 三、解答题（本大题共6小题，共80分.解答应写出文字说明，证明过程或演算步骤）‎ ‎15．已知函数f（x）=sinxcosx+cos（π﹣x）cosx ‎（Ⅰ）求f（x）的最小正周期；‎ ‎（Ⅱ）求f（x）在区间[0，]上的最大值和最小值．‎ ‎【考点】GL：三角函数中的恒等变换应用；H2：正弦函数的图象．‎ ‎【分析】（Ⅰ）利用二倍角以及辅助角公式基本公式将函数化为y=Asin（ωx+φ）的形式，再利用周期公式求函数的最小正周期．‎ ‎（Ⅱ）x∈[0，]上时，求出内层函数的取值范围，结合三角函数的图象和性质，即得f（x）的最大值和最小值．‎ ‎【解答】解：函数f（x）=sinxcosx+cos（π﹣x）cosx 化简可得：f（x）=sin2x﹣cos2x=sin2xcos2x﹣=sin（2x﹣）‎ ‎（Ⅰ）f（x）的最小正周期T=‎ ‎（Ⅱ）∵x∈[0，]上，‎ ‎∴2x﹣∈[，]‎ 当2x﹣=，即x=0时，函数f（x）取得最小值为．‎ 当2x﹣=，即x=时，函数f（x）取得最大值为1﹣．‎ ‎∴f（x）在区间[0，]上的最大值为1﹣，最小值为．‎ ‎　‎ ‎16．已知数列{an}满足：a1=1，an+1=2an，数列{bn}满足：b1=3，b4=11，且{an+bn}为等差数列．‎ ‎（I） 求数列{an}和{bn}的通项公式；‎ ‎（II） 求数列{bn}的前n项和．‎ ‎【考点】8E：数列的求和；8H：数列递推式．‎ ‎【分析】（Ⅰ）利用等差数列、等比数列的通项公式先求得公差和公比，即可求数列的通项公式；‎ ‎（Ⅱ）利用分组求和的方法求解数列的和，由等差数列及等比数列的前n项和公式即可求解数列的和．‎ ‎【解答】解：（I）因为在数列{an}中，a1=1，an+1=2an 所以， =2，n∈N*，‎ 即数列{an}是以首项为1，公比为2的等比数列．‎ 所以an=2n﹣1‎ 设等差数列{an+bn}的公差为d，‎ 由题意得：3d=（a4+b4）﹣（a1+b1 ）=（23+11）﹣（1+3）=15‎ 解得d=5，‎ ‎∴an+bn=4+5（n﹣1）=5n﹣1，‎ ‎∴bn=5n﹣1﹣2n﹣1，‎ ‎（II） 由（I）知bn=5n﹣1﹣2n﹣1，‎ 数列{5n﹣1}的前n项和为4n+=n2+n．‎ 数列{2n﹣1}的前n项和为=2n﹣1，‎ 所以，数列{bn}的前n项和n2+n﹣2n+1．‎ ‎　‎ ‎17．某高中学校为了解学生体质情况，从高一和高二两个年级分别随机抽取了40名男同学进行“引体向上”项目测试．样本的测试成绩均在0至30个之间，按照[0，5），[5，10），[10，15），[15，20），[20，25），[25，30]的分组分别作出频率分布直方图．记样本中高一年级的“引体向上”成绩的方差为s12，高二年级的“引体向上”成绩的方差为s22．‎ ‎（Ⅰ）已知该学校高二年级男同学有500人，估计该学校高二年级男同学引体向上成绩不少于10个的人数；‎ ‎（Ⅱ）从样本中高一年级的成绩不小于20个男同学中随机抽取2人，求至少有1人成绩在[25，30]中的概率．‎ ‎（Ⅲ）比较s12与s22的大小（只需写出结果）．‎ ‎【考点】CC：列举法计算基本事件数及事件发生的概率；B8：频率分布直方图．‎ ‎【分析】（Ⅰ）先求出样本中高二年级男同学引体向上成绩不少于10个的频率，由此能估计该学校高二年级男同学引体向上成绩不少于10个的人数．‎ ‎（Ⅱ）记“从样本中高一年级的成绩不小于20个的同学中随机抽取2人，至少有1人成绩在[25，30]中”为事件M，样本中高一年级的成绩在[20，25）的人数为4人，记这4名同学为A1，A2，A2，A4，样本中高一年级的成绩在[25，30]的人数为2人，记这两名同学为B1，B2，由此利用列举法能求出至少有1人成绩在[25，30]中的概率．‎ ‎（Ⅲ）由频率分布直方图能比较，的大小．‎ ‎【解答】解：（Ⅰ）因为样本中高二年级男同学引体向上成绩不少于10个的频率为（0.08+0.04+0.01）×5=0.65，‎ 所以估计该学校高二年级男同学引体向上成绩不少于10个的人数为：‎ ‎500×0.65=325人．‎ ‎（Ⅱ）记“从样本中高一年级的成绩不小于20个的同学中随机抽取2人，‎ 至少有1人成绩在[25，30]中”为事件M，‎ 样本中高一年级的成绩在[20，25）的人数为40×0.02×5=4人，‎ 记这4名同学为A1，A2，A2，A4，‎ 样本中高一年级的成绩在[25，30]的人数为40×0.01×5=2人，‎ 记这两名同学为B1，B2，‎ 则从样本中高一年级的成绩不小于20个的同学中，随机抽取2人，所有可能的结果有15种，分别为：‎ ‎（A1，A2），（A1，A3），（A1，A4），（A1，B1），（A1，B2），‎ ‎（A2，A3），（A2，A4），（A2，B1），（A2，B2），（A3，A4），‎ ‎（A3，B1），（A3，B2），（A4，B1），（A4，B2），（B1，B2），‎ 事件M包含的结果有9种，分别是：‎ ‎（A1，B1），（A1，B2），（A2，B1），（A2，B2），（A3，B1），‎ ‎（A3，B2），（A4，B1），（A4，B2），（B1，B2），‎ 所以至少有1人成绩在[25，30]中的概率P（M）=．‎ ‎（Ⅲ）＞．‎ ‎　‎ ‎18．如图，正三角形ABE与菱形ABCD所在的平面互相垂直，AB=2，∠ABC=60°，M是AB的中点，N是CE的中点．‎ ‎（I）求证：EM⊥AD；‎ ‎（II）求证：MN∥平面ADE；‎ ‎（III）求点A到平面BCE的距离．‎ ‎【考点】LS：直线与平面平行的判定；MK：点、线、面间的距离计算．‎ ‎【分析】（Ⅰ）推导出EM⊥AB，从而EM⊥平面ABCD，由此能证明EM⊥AD．‎ ‎（Ⅱ）取DE的中点F，连接AF，NF，推导出四边形AMNF是平行四边形，从而MN∥AF，由此能证明MN∥平面ADE．‎ ‎（III）设点A到平面BCE的距离为d，由VA﹣BCE=VE﹣ABC，能求出点A到平面BCE的距离．‎ ‎【解答】证明：（Ⅰ）∵EA=EB，M是AB的中点，∴EM⊥AB，‎ ‎∵平面ABE⊥平面ABCD，平面ABE∩平面ABCD=AB，EM⊂平面ABE，‎ ‎∴EM⊥平面ABCD，‎ ‎∵AD⊂平面ABCD，∴EM⊥AD．‎ ‎（Ⅱ）取DE的中点F，连接AF，NF，‎ ‎∵N是CE的中点．，∴NFCD，‎ ‎∵M是AB的中点，∴AM，‎ ‎∴NFAM，∴四边形AMNF是平行四边形，‎ ‎∴MN∥AF，‎ ‎∵MN⊄平面ADE，AF⊂平面ADE，‎ ‎∴MN∥平面ADE．‎ 解：（III）设点A到平面BCE的距离为d，‎ 由（I）知ME⊥平面ABC，BC=BE=2，MC=ME=，‎ 则CE=，BN==，‎ ‎∴，‎ ‎=，‎ ‎∵VA﹣BCE=VE﹣ABC，即，‎ 解得d=，故点A到平面BCE的距离为．‎ ‎　‎ ‎19．已知函数f（x）=1+lnx﹣aex ‎（Ⅰ）若曲线y=f（x）在x=1处的切线与x轴平行，求实数a的值；‎ ‎（Ⅱ）若对任意x∈（0，+∞），不等式f（x）≤0恒成立，求实数a的取值范围．‎ ‎【考点】6E：利用导数求闭区间上函数的最值；6H：利用导数研究曲线上某点切线方程．‎ ‎【分析】（Ⅰ）根据导数和几何意义即可求出，‎ ‎（Ⅱ）分离参数，构造函数，利用导数，求出函数的最值，即可求出参数的取值范围 ‎【解答】解：（Ⅰ）∵f（x）=1+lnx﹣aex，‎ ‎∴f′（x）=﹣aex，x∈（0，+∞）．‎ 由于曲线y=f（x）在x=1处的切线与x轴平行，‎ ‎∴f′（1）=1﹣ae=0，‎ 解得，‎ ‎（Ⅱ）由条件知对任意x∈（0，+∞），不等式f（x）≤0恒成立，‎ 此命题等价于a≥对任意x∈（0，+∞）恒成立 令，x∈（0，+∞）．‎ ‎∴=（﹣1﹣lnx），x∈（0，+∞）．‎ 令g（x）=（﹣1﹣lnx），x∈（0，+∞）．‎ 则g′（x）=﹣﹣＜0．‎ ‎∴函数g（x）在x∈（0，+∞）上单调递减．‎ 注意到g（1）=0，即x=1是g（x）的零点，‎ 而当x∈（0，1）时，g（x）＞0；当x∈（1，+∞）时，g（x）＜0．‎ 又ex＞0，所以当∈（0，1）时，h′（x）＞0；当x∈（1，+∞）时，h′（x）＜0．‎ 则当x变化时，h′（x）的变化情况如下表：‎ x ‎（0，1）‎ ‎1‎ ‎（1，+∞）‎ h′（x）‎ ‎+‎ ‎0‎ ‎﹣‎ h（x）‎ ‎↗‎ 极大值 ‎↘‎ 因此，函数h（x）在x∈（0，+∞），取得最大值，所以实数a≥．‎ ‎　‎ ‎20．已知椭圆C： +=1（a＞b＞0）经过点（1，），离心率e=．‎ ‎（Ⅰ）求椭圆C的方程，‎ ‎（Ⅱ）设动直线l：y=kx+m与椭圆C相切，切点为T，且直线l与直线x=4相交于点S．试问：在坐标平面内是否存在一定点，使得以ST为直径的圆恒过该定点？若存在，求出该点的坐标；若不存在，请说明理由．‎ ‎【考点】KL：直线与椭圆的位置关系．‎ ‎【分析】（Ⅰ）由题意可知：将点代入椭圆方程，利用椭圆的离心率公式即可求得a和b的值，即可求得椭圆方程；‎ ‎（Ⅱ）将直线方程代入椭圆方程，由△=0，求得4k2﹣m2+3=0，利用韦达定理及中点坐标公式，求得T点坐标，联立即可求得S点坐标，由•=0，根据向量数量积的坐标运算，可得，即可求得A点坐标，即可求得以ST为直径的圆恒过该定点（1，0）．‎ ‎【解答】解：（Ⅰ）由点（1，）在椭圆上得，代入椭圆方程：，①‎ ‎﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣‎ 椭圆的离心率e==，则a=2c，a2=4c2，b2=3c2，②﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣‎ ‎②代入①解得c2=1，a2=4，b2=3，‎ 故椭圆C的标准方程为；﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣‎ ‎（Ⅱ）由，消去y，整理得（4k2+3）x2+8kmx+4m2﹣12=0；‎ 因为动直线l与椭圆C相切，即它们有且只有一个公共点T，可设T（x0，y0），‎ m≠0，△=0，∴（8km）2﹣4×（4k2+3）×（4m2﹣12）=0，‎ ‎∴4k2﹣m2+3=0，③﹣﹣﹣﹣‎ 此时，x0==﹣=﹣，y0=kx0+m=，则T（﹣，）．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣‎ 由，得S（4，4k+m）．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣‎ 假设平面内存在定点满足条件，不妨设为点A．‎ 由图形对称性知，点A必在x轴上．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣‎ 设A（x1，0），则由已知条件知AS⊥AT，‎ 即•=0对满足③式的m，k恒成立．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣‎ 由=（4﹣x1，4k+m），=（﹣﹣x1，），由•=0得：﹣ +‎ ‎﹣4x1+x12++3=0，‎ 整理得（4x1﹣4）+x12﹣4x1+3=0，④﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣‎ 由②式对满足①式的m，k恒成立，则，解得x1=1．‎ 故平面内存在定点（1，0），使得以ST为直径的圆恒过该定点．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣‎ ‎　‎ ‎2017年6月15日